Данная информация предназначена для специалистов в области здравоохранения и фармацевтики. Пациенты не должны использовать эту информацию в качестве медицинских советов или рекомендаций.
Закономерности целостного организма
А. А. Хускивадзе1, А. П.
Хускивадзе
1) Посмертно.
Аннотация.
В статье изложена математическая модель живого организма как единого целого.
Введено понятие степени здоровья и дано обоснование
способов определения:
1) предельно допустимых значений первичных
показателей состояния здоровья человека,
2) степени здоровья человека,
3) степени переносимости врачебных и других
воздействий организмом (СПЕВО) человека.
Установлены закономерности, которыми управляются
процессы, происходящие в живом организме.
Статья представляет интерес для специалистов, работающих на стыке
фундаментальной медицины, биологии, физики и философии.
Все права на материалы статьи защищены, и эти
материалы не могут быть использованы без письменного разрешения
владельцев авторских прав.
Ключевые слова: живой организм, математическое
моделирование, количественные показатели состояния здоровья, свертка частных
показателей, объективные характеристики состояния здоровья.
Введение
В современной доказательной медицине внимание
сосредоточено, главным образом, на статистических методах обоснования принятия
врачебных решений [1], [2], [3]. Без применения этих методов сегодня
трудно говорить об объективности принятия врачебных решений. Далее мы будем
полагать, что обследование человека выполнено с применением этих методов.
Способ, предложенный ниже, является следующим
этапом на пути объективизации принимаемых врачебных решений.
Первая версия этого способа была применена в
изобретении [4]. Эта версия предполагает
наличие большой статистики, и она нами применялась в медицинской науке. С ее
помощью были, в частности, выполнены исследования [5], [6], [7], [8],
[9].
Последующая, улучшенная версия способа нашла
примененные в работах [10] и [11].
Ниже излагается последняя–наиболее совершенная–версия
способа. Эта версия является наиболее совершенной в том смысле, что
1 Она применима даже в том случае, когда в
распоряжении специалиста имеются единичные результаты обследования человека.
Следовательно, этим способом можно оперировать в медицинской практике при
обосновании принимаемого врачебного решения.
2.С ее помощью степени здоровья человека
определяют с учетом и индивидуальных норм этого человека.
Разумеется, эта версия способа применима и в
медицинской науке. На ее основе созданы изобретения [12]
и [13].
1.Нормальный уровень функционирования физиологических систем организма.
Нормальное состояние и состояние покоя
В основе материалов, изложенных ниже, лежит
положение о нормальном уровне функционирования физиологических систем организма,
сформулированное акад. Р.М. Баевским. Он пишет: «Обычный
(нормальный, средний) уровень функционирования физиологических систем означает
минимальное (или оптимальное) взаимодействие высших и низших уровней
управления. Автономность низших уровней освобождает от необходимости постоянно
участвовать в локальных регуляторных процессах. Вмешательство высших уровней (механизмов)
управления в работу низших происходит только
в том случае, когда поток информации (энергии, вещества) превышает возможность
управляющего механизма. Такое вмешательство становится необходимым и в случае
нарушения взаимной координации нескольких подсистем (контуров, механизмов)
низшего уровня.
Оптимальное сочетание принципов централизации и
автономности управления в живом организме обеспечивает максимальную
адаптивность целостной системы при ее взаимодействий
с факторами внешней среды. Следовательно,
автономная деятельность внутренних механизмов управления означает оптимальное
сочетание их активностей в соответствии с задачами целостной системы,
определяемыми сочетанием внешних механизмов» [14, с.77-78].
Из выше изложенного следует, что:
1. В нормальном состоянии может находиться
только здоровый человек.
2. Если
состояние человека нормальное,
то его организм тратит минимальную энергию.
В этом случае говорят, что человек находится в
состоянии п о к о я. Во всех других случаях человек находится в
ненормальном состоянии, т.е. на его организм производится некоторое –внутреннее
и/или внешнее –воздействие.
3. Если человек находится в нормальном
состоянии, то локальные функциональные системы саморегулирования его
организма работают автономно, т.е.
самостоятельно, а центральные функциональные
системы регулирования только следят за тем, как локальные системы справляются со
своими обязанностями.
Следовательно, если центральные функциональные
системы регулирования организма человека вмешиваются в работу той или иной
локальной функциональной системы, то это означает, что организм человека
находится в ненормальном состоянии, т.е. человек либо болен, либо он здоров, но
выполняет некоторую (умственную или физическую) работу.
Человек является здоровым, если он находится в
нормальном состоянии, либо его состояние является ненормальным, но эта
ненормальность вызвана лишь воздействием извне и она существует до тех
пор, пока не устранено внешнее воздействие.
Если в ненормальном состоянии организм человека
находится по причине внутреннего воздействия или совокупности внутреннего
и внешнего воздействий, то говорят, что человек болен.
Состояние больного человека всегда является
ненормальным. При этом больной
может находиться в покое или нет. Больной находится в покое, если его организм
подвергается таким внешним воздействиям, при которых состояние здорового
человека соответствующего пола и возрастной группы является нормальным.
2. Объективные и субъективные характеристики
состояния здоровья человека
Обозначим через A генеральная совокупность,
составленная людьми, для которых имеют место:
C(a, A,G) = C(A,G); a = 1..N(A)
и (2.1)
Y(r,a,A,G) = Y(r,A,G); a = 1..N(A); r = 0..N(A,G) ,
где
C(a, A,G)
– генеральная совокупность всевозможных –
нормального и ненормальных - состояний организма человека a
Î A;
C(A,G) –
фиксированное значение C(a,A,G)
для множество людей A;
N(A) – объем A;
Y(r,a,A,G)
– генеральная совокупность первичных
показателей r – го возможного состояния организма
человека a Î A;
Y(r,A,G)
– фиксированное значение Y(r,a,A,G)
для множество людей A,
когда они находятся в r-ом
состоянии;
N(A,G) – объем C(A,G);
Для определенности положим, что если человек a
Î A
находится в нормальном состоянии, то
r = 0 и, следовательно,
имеет место
Y(0,a,A,G) = Y(0,A,G),
где
Y(0,a,A,G)
– генеральная совокупность первичных
показателей нормального состояния организма человека a
Î A;
Y(0,A,G)
– фиксированное значение Y(0,a,A,G)
для множества людей A,
когда они находятся в нормальном состоянии.
Пусть, Y – совокупность показателей ф а к т и ч е с к о г о состояния
здоровья человека, а N–объем
Y.
В том случае, когда речь идет об одном
конкретном состоянии одного определенного человека, т.е. когда имеет место
A = A0; a = a0 и
r = r0; a0 = 1..N(A); r0 = 1..N(A,G)
для простоты записи можно пользоваться обозначениями:
Y = Y(0,A,G) = Y(G) и N = N(0,A,G) =
N(G), если r = 0
и (2.2)
Y = Y(r,A,G) = Y(O,G) Í Y(G) и
N = N(r,A,G) = N(O,G) ≤ N(G), если r > 0,
где
A0 , a0
и r0 –
фиксированные значения A, a
и r
соответственно;
Y –генеральная
совокупность показателей фактического состояния здоровья человека
a Î A;
Y(G) –
генеральная совокупность показателей
нормального состояния здоровья человека;
N – объем
Y;
N(G) –
объем Y(G);
Y(O,G) – генеральная
совокупность первичных показателей состояния здоровья человека a
Î A,
которые для множество людей
A(a,G) при данном
ненормальном состоянии вообщее бывают
отклоненными от своих норм;
A(a,G) –
однородное множество людей, которые относятся к той
же поло –возрастной группе, к которой относится человек a
Î A;
N(O,G)
–объем1 Y(O,G).
Пусть
bjlr(a) ;l= 1..Njr(a);
j = 1..N; r = 0..N(A,G)
является совокупностью результатов обследования фактического
состояния здоровья человека
a Î A(r,A,G),
где
A(r,A,G)
– однородная совокупность, составленная людьми из
A, которые находятся
в r-ом состоянии.
Положим, что выполняются следующие условия.
Условие 1
Каждая выборка
Bjr(a) = {bjl
r(a) ;
l = 1..Njr(a)}
; j = j0;
r = r0;
j0 = 1..N; r0
= 0..N(A,G)
представляет собой совокупностью результатов
равноточных и независимых измерений величины
yj Î Y.
Условие 2.
Систематические ошибки измерения величины
yj Î Y
отсутствуют, а случайные ошибки ее измерений
описываются нормальным распределением вероятностей.
Условие 3.
С доверительной вероятностью
P » 1
можно утверждать, что совокупность
Bj1(a)
является репрезентативной выборкой из Bjr(a,G)
Í Bjr(a,G,¥
),
где
Bjr(a,G)
– генеральная совокупность значений величины
yj Î Y,
различаемых друг от друга в организме
человека a Î A(r,A,G)
в момент времени T;
________________________________________
1) В обозначениях N(0,A,G)
и N(O,G)
используются индексы «0» и «O»
соответственно, где «O»
- первая буква русского слова «Отклонение»
Bjr(a,G,¥
) – генеральная совокупность возможных
значений величины yj Î
Y для организма человека a
Î A(r,A,G)
в момент времени T.
Совокупность Bjr(a,G,¥
) при одном уровне развития технических средств
измерения является одной, при другом уровне – другой и т.д. Однако, в момент
времени T, т.е. когда
изучается состояние здоровья данного человека, можно считать, что совокупность
Bjr(a,G,¥
) является вполне определенной, но не обязательно
нам известной.
Множество Bj0(a,G)
представляет собой генеральную совокупность
значений величины
yj Î Y,
различаемых друг от друга в организме
человека aÎ A
при r = 0,
т.е.
когда этот человек находится в нормальном
состоянии.
Вообще
Bjr(a,G) Í Bj0(a,G)
Í Bj0(a,G,¥ );
j = 1..N(G),
где
Bj0(a,G,¥
) – генеральная совокупность возможных значений величины yj
Î Y для организма
человека aÎ A
в нормальном состоянии.
Величины
Bj0(a), bjl 0(a)
и Nj0(a)
по определению являются значениями
Bjr(a),
bjl r(a)
и Njr(a)
такими, что
Bjr(a) = Bj0(a) ; bjl
r(a) = bjl 0(a)
и Njr(a)
= Nj0(a)
при Bjr(a,G) = Bj0(a,G) (2.3)
Обозначим
 и
и
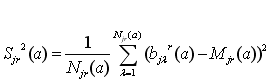
и (2.4)
djr(a) = Sjr(a)
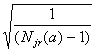 и tjr(a)= tj(P, (Njr(a)
– 1)),
и tjr(a)= tj(P, (Njr(a)
– 1)),
где
tjr(a) - критическое
значение критерия Стьюдента при степени свободы (Njr(a)
– 1).
Если все выше перечисленные три условия выполняются и при этом
djr(a)
tjr(a) > 0, (2.5)
, то с вероятностью P
» 1 можно утверждать,
что [15]:
1.Имеет место
ç Μjr(a) - Μjr(a,G,¥
) ç < djr(a)
tjr(a), (2.6)
где
Μjr(a,G,¥
) – значение Μjr(a)
такое, что
Μjr(a) = Μjr(a,G,¥
) при Bjr(a) = Bjr(a,G,¥
)
2.Выполняется условие
Y(O,G) = Æ Û
ç Μj1(a) - Μj0(a)
ç < d
jr*(a) t jr*(a)
для всех j = 1..N(G), (2.7)
где
d jr*(a) =
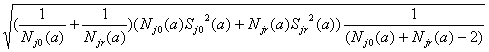
и (2.8)
t jr*(a) =
t j(P, (Nj0(a)
+ Njr(a)
– 2)).
Здесь через t j*обозначено
критическое значение критерия Стьюдента при степени
свободы (Nj0(a)
+ Njr(a)
– 2).
Совокупности
Bjr(a); r = 1..N(a,C); j = 1..N(A)
при одной P являются одними, при другой
P – другими и т.д.
Следовательно, величины
P, Μjr;
Sjr и
Njr (2.9)
являются субъективными характеристиками состояния здоровья человека.
Пусть
P(a,G), Μjr(a,G); Sjr(a,G)
и Njr(a,G)
-значения величин (2.9)
такие, что
P(a,G) = P; Μjr = Μjr(a,G);
Sjr = Sjr(a,G) и Njr = Njr(a,G)
при Bjr(a) = Bjr(a,G); j =1..N,
(2.10)
где
Njr(a,G) – объем Bjr(a,G).
Совокупности
Bjr(G);
j =1..N,
как указывалось выше, для организма человека в каждый момент времени
T являются вполне
определенными.
Следовательно, величины
P(a,G),
Μjr(a,G);
Sjr(a,G)
и Njr(a,G);
j =1..N (2.11)
для организма aÎ A
в каждый момент времени T
также являются вполне определенными, т.е. они
являются объективными характеристиками состояния здоровья этого человека.
В случаях, когда Y(O,G)
= Æ , каждая величина
yjÎ Y
принимает значения, близкие
к Μj0(G) >
0. Благодаря этому всегда имеет место
Sjr(a,G)
³ Sj0(a,G)
> 0; j =1..N(G)
Кроме этого, имеет место
Njr(a,G)
£ Nj0(a,G)
; j =1..N(G),
ибо нормальное состояние организма человека является его обычным, т.е.
наиболее часто встречаемым состоянием.
В итоге
Sjr(a,G) ³ Sj0(a,G)
> 0 и Njr(a,G)
£ Nj0(a,G) (2.12)
3. Индивидуальная норма человека.
В нормальном состоянии в организме человека
преобладают процессы, направленные на сохранение этого состояния. Другое дело,
когда человек не находится в нормальном состоянии. В этом случае в организме
человека могут преобладать либо процессы, которые направлены на возращение
организма в нормальное состояние, либо же – процессы, которые не направлены на
возращенные организма в нормальное состояние.
В том случае, когда в организме преобладают
процессы, которые направлены на его возращение в нормальное состояние, говорят,
что организм на воздействия – внешние и/или внутренние - реагирует адекватно. Во
всех других случаях говорят, что организм на
воздействия не реагирует адекватно.
Обозначим через B0(a)
и B1(a)
соответственно события:
«В организме преобладают процессы, которые
направлены на сохранение или возвращение его в нормальное состояние»
и
«В организме преобладают
процессы, которые не направлены на сохранение
или возвращение его в нормальное состояние»
Для этих событий, как взаимопротивоположных,
имеют место
B0(a)P B1(a)
= Æ
и (3.1)
P(B0(a)) + P(B1(a)) = 1,
где
P(B0(a))
– вероятность наступления события
B0(a);
P(B1(a))
– вероятность наступления события
B1(a).
Предположим, что человек
aÎ A всегда
находятся в нормальном состоянии. Тогда будет иметь место:
P(B0(a))
= 1. А в этом случае не будет никакой необходимости
проверки состояния здоровья ‘этого человека. Следовательно, обследуя
состояние здоровья человека aÎ A,
мы, тем самим полагаем, что
P(B0(a))
< 1 .
Определение 1.
Пусть, в момент времени T
имеет место
P(B0(a)) = Pmax(B0(a)),
где
Pmax(B0(a))
– значение P(B0(a))
для организма человека aÎ A
в нормальном состоянии:
P(B0(a))
≤ Pmax(B0(a))
< 1 (3.2)
Тогда и только тогда говорят, что:
1. Решение, принимаемое организмом человека
aÎ A
в момент времени T,
является наиболее обоснованным.
2. Величина P(B0(a))
является вероятностью принятия организмом человека
aÎ A
наиболее обоснованного решения в момент времени
T.
Согласно (3.1)
и (3.2) имеет
место
P(B1(a))
> 0 .
Определение 2.
Пусть, в момент времени T
имеет место
P(B1(a)) = Pmin(B1(a)),
где
Pmin(B1(a))
– значение P(B1(a))
для организма человека aÎ A
в нормальном состоянии:
0 < Pmin(B1(a))
≤ P(B1(a))
(3.3)
Тогда и только тогда говорят, что:
1. Решение, принимаемое организмом человека
aÎ A
в момент времени T,
является наименее обоснованным.
2. Величина Pmin(B1(a))
является вероятностью принятия организмом человека
aÎ A
наименее обоснованного решения в момент времени
T.
Ясно, что чем больше величина
P(B0(a)),
тем чаще
организм человека aÎ A
будет находиться в нормальном состоянии. И,
наоборот, чем чаще организм человека
находится в нормальном состоянии, тем больше будет
величина P(B0(a)).
С этой точки зрения о величине
P(B0(a))
можно говорить, что она является
вероятностной мерой близости фактического состояния человека aÎ
A к его возможному нормальному
состоянию.
Определение 3
Пусть, имеют место зависимости (3.1)
и (3.2).
Тогда и только тогда говорят, что величина
P(B0(a))
является вероятностной мерой близости
фактического состояния человека aÎ A
к его возможному нормальному состоянию и
пишут:
P(a,G) º P(B0(a)) и
P(a,G) = Pmax(B0(a)), (3.4)
где
P(a,G) –вероятностная
мера близости фактического состояния здоровья человека aÎ
A к его возможному нормальному состоянию:
P = P(0,a,G) при Bjr(a) = Bjr(0,a,G)
для всех r =0..N(a,G) и
j =1..N; (3.5)
P(0,a,G) -
значение P(a,G)
для организма человека aÎ A
в нормальном состоянии:
P(0,a,G)
= Pmax(B0(a)).
Нормальное состояние является е с т е с т в е н н ы м, т. е. п р е о б л а д
а ю щ и м с о с т о я н и е м о р г а н и з
м а т и п и ч н о г о п р е д с т а в и т е л я
людей для каждой поло-возрастной группы.
Следовательно
Pmax(B0(a))
³ Pmax(B1(a))
(3.6)
Эта зависимость, как видно, указывает на то, что
в общем случае событие B0(a)
происходит более часто, чем событие B1(a).
С учетом (3.6)
из (3.1) и
(3.2) получаем
0 < P(B1(a))
£ 0.5 и 0.5 £
P(B0(a))
< 1 (3.7)
При этом, согласно (3.1), выполняется условие
P(B0(a))
= 0.5 Û P(B1(a))
= 0.5 (3.8)
Согласно (3.2), (3.3), (3.4) и (3.7) имеет место
0 < Pmin(B1(a))
≤ P(B1(a))
≤ 0.5 и 0.5 ≤ P(a,G)
≤ P(0,a,G)
< 1 (3.9)
Положим, что
r = r0;
r0 = 0..N(a,C) (3.10)
и введем обозначения
Μj1(a,G) = Μjr(a,G);
Sj1(a,G) = Sjr(a,G) и Nj1(a,G)
= Njr(a,G)
при r = r0;
r0 = 0..N(a,C)
(3.11)
Согласно (2.12), (3.10) и (3.11) имеет место
Sj1(a,G) ³ Sj0(a,G)
> 0 и Nj1(a,G)
£ Nj0(a,G) (3.12)
Пусть, A(0,a,G)
– однородная совокупность, составленная
людьми той поло-возрастной группы, к которой в нормальном состоянии
человек aÎ A
принадлежит.
Положим, что A(0,a,G)
является генеральной совокупностью.
Обозначим
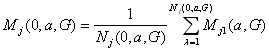
и (3.13)
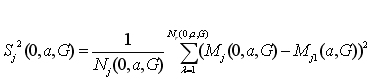
где
N(0,a,G) – объем A(0,a,G).
Величины
Μj(0,a,G); Sj(0,a,G) и
N(0,a,G)
являются объективными характеристиками типичного
представителя (ТП)
множества людей A(0,a,G).
О величине Μj(0,a,G)
говорят, что она является статистической точечной нормой человека a
Î Aj(0,a,G)/
Согласно (2.3), (2.8), (2.10), (3.5) и (3.11)
имеет место
d jr*(a)
= d j*(a,G)
и t jr*(a)
= t j*(a,G),
где
d j*(a,G) =
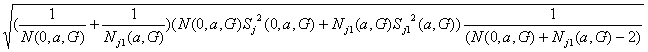
и (3.14)
t j*(a,G) =
t j(P(G), (N(0,a,G) + Nj1(a,G)
– 2)).
Обозначим
d j0*(a,G) = Sj(0,a,G)
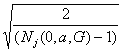 и
t j0*(0,a,G) = tj(P(G),
2 (Nj(0,a,G) – 1))
и
t j0*(0,a,G) = tj(P(G),
2 (Nj(0,a,G) – 1))
и (3.15)
d j1*(a,G) = Sj1(a,G)
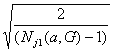 и
t j1*(a,G) =
t j(P(G), 2 (Nj1(a,G)
– 1));
и
t j1*(a,G) =
t j(P(G), 2 (Nj1(a,G)
– 1));
d j(a,G) = d
j1*(a,G) и t
j(a,G) = t j1*(a,G)
при d j1*(a,G)
t j1*(a,G) ≤
d j*(a,G) t
j*(a,G)
и (3.16)
d j(a,G) = d
j*(a,G) и t
j(a,G) = t j*(a,G)
при d j1*(a,G)
t j1*(a,G) >
d j*(a,G) t
j*(a,G)
Согласно (3.15) и (3.16) имеет место
d j(a,G)
t j(a,G)
≤ d j*(a,G)
t j*(a,G)
(3.17)
и, следовательно,
A(d j(a,G) t
j(a,G)) Í A(d
j*(a,G) t j*(a,G)),
(3.18)
где
A(d j(a,G) t
j(a,G)) = {Μj(0,a,G) -
d j(a,G) t
j(a,G), Μj(0,a,G) +
d j(a,G) t j(a,G)}
и (3.19)
A(d j*(a,G)
t j*(a,G)) = {Μj(0,a,G)
- d j*(a,G)
t j*(a,G), Μj(0,a,G)
+ d j*(a,G)
t j*(a,G)}
Определение 4
Пусть, в момент времени T
имеет место
Μj1(a,G)
Î A(d j*(a,G)
t j*(a,G)) для
всех j = 1..N(G) (3.20)
Тогда и только тогда с вероятностью P(a,G)
утверждают, что в момент времени T
человек a
Î A находится в нормальном
состоянии в обычном смысле.
Об области
A(d j*(a,G)
t j*(a,G)); j = j0;
j0 = 1..N(a,G)
говорят, что в момент времени T
она является областью индивидуальной нормы человека
a Î A
в обычном смысле..
Определение 5
Пусть, в момент времени T
имеет место
Μj1(a,G) Î A(d
j(a,G) t j(a,G)) для
всех j = 1..N(G) (3.21)
и, следовательно, согласно (3.18), выполняется условие (3.20).
Тогда и только тогда с вероятностью P(a,G)
утверждают, что в момент времени T
человек a
Î A находится в нормальном
состоянии в широком смысле.
Об области
A(d j(a,G) t
j(a,G)); j = j0; j0 = 1..N(a,G) (3.22)
говорят, что в момент времени T
она является областью индивидуальной нормы человека
a Î A
в широком смысле.
О величине Μj1(a,G)
говорят, что в момент времени
T она является точечной индивидуальной нормой человека a
Î A
и пишут:
Μj1(a,G)
= Μj0(a,G)
(3.23)
Согласно (3.21) и (3.23) вообще имеет место
Μj1(a,G) = Μj0(a,G)
Û Μj1(a,G)
Î A(d j(a,G)
t j(a,G)) (3.24)
Обозначим
dj1(a,G) = Sj1(a,G)
 и
tj1(a,G) = tj(P(a,G), (Nj1(a,G)
– 1))
и
tj1(a,G) = tj(P(a,G), (Nj1(a,G)
– 1))
и (3.25)
dj(0,a,G) = Sj(0.a,G)
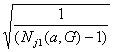 и
tj(0,a,G) = tj(P(a,G), (Nj(0,a,G)
– 1))
и
tj(0,a,G) = tj(P(a,G), (Nj(0,a,G)
– 1))
Пусть,
Μj0(0,a,G)
– значение Μj0(a,G)
такое, что
Μj0(a,G) = Μj0(0,a,G)
Û dj1(a,G) tj1(a,G) ≤ dj(0,a,G)
tj(0,a,G)
О величине Μj0(0,a,G)
говорят, что она является е с т е с т в е н н ы м г
л о б а л ь н ы м о п т и м у м о м величины yj
для организма человека a Î
A в момент времени
T. Она является глобальным
оптимумом в том смысле, что
Μi1(0,a,G) = Μi0(0,a,G)
Û Μj1(0,a,G) =
Μj0(0,a,G) для
всех i,j = 1..N(G)
или, более корректно,
ê Μi1(0,a,G) -
Μi0(0,a,G) ê < di1(a,G)
ti1(a,G) Û ê
Μj1(0,a,G) –
- Μj0(0,a,G) ê <
dj1(a,G) tj1(a,G) для всех
i,j = 1..N(G) (3.26)
О значении величины P(a,G),
для которой выполняется условие (3.26), говорят,
что она является в е р о я т н о с т н ы м п р е д е л о м п о з н а н и я и с т
и н ы в организме человека a Î
A в момент времени
T.
Подробное обоснование понятия вероятностного предела познания истины
приведено в [12], [16] и [17].
4. Главный признак целостности живого организма.
Теория В.Г. Афанасьева
Положим, что
a = a0;
a0 = 1..N(A)
(4.1)
и обозначим
Μj(0,G),
Sj(0,G),
Nj(0,G), Μj1(G),
Sj1(G)
и Nj1(G)
значения величин
Μj(0,a,G), Sj(0,a,G), Nj(0,a,G),
Μj1(a,G), Sj1(a,G) и
Nj1(a,G),
такие, что
Μj(0,a,G) = Μj(0,G);
Sj(0,a,G) = Sj(0,G); Nj(0,a,G) = Nj(0,G)
и при a = a0 (4.2)
Μj1(a,G) = Μj1(G);
Sj1(a,G) = Sj1(G); Nj1(a,G) = Nj1(G)
Согласно (3.14), (3.15), (3.16), (4.1) и
(4.2) имеют место
d j*(a,G) =
d j*(G); t
j*(a,G) = t j*(G);
d jk*(a,G) =
d jk*(G); t
jk*(a,G) = t jk*(G)
и (4.3)
d j(a,G) = d
j(G) и t j(a,G)
= t j(G)
где
d j*(G) =
= 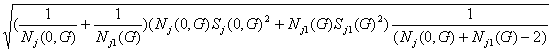
и (4.4)
t j*(G) =
t (P(G), (Nj(0,G)
+ Nj1(G)
– 2));
d j(G) = d
j1*(G) и t
j(G) = t j1*(G)
при d j1*(G)
t j1*(G) ≤
d j*(G) t j*(G)
и (4.5)
d j(G) = d
j*(G) и t
j(G) = t j*(G)
при d j1*(G)
t j1*(G) >
d j*(G) t j*(G),
где
d j1*(G) = Sj1(G)
 и
t j1*(G) =
t j(P(G), 2 (Nj1(G)
– 1)) (4.6)
и
t j1*(G) =
t j(P(G), 2 (Nj1(G)
– 1)) (4.6)
Согласно (4.5) имеет место
d j(G)
t j(G)
≤ d j*(G)
t j*(G)
(4.7)
Пусть
g (G)
и g
j(G) ;
j = 1..N(G)
являются вещественными величинами такими, что
выполняются следующие условия:
1.Имеют место
g (G) = f(Μj1(G),
Sj1(G),
Nj1(G),
Μj0(G),
Sj0(G),
Nj0(G));
j = 1..N(G))Î
[0,1]
(4.8)
g j(G)
= fj(Μj1(G),
Sj1(G),
Nj1(G), Μj0(G),
Sj0(G),
Nj0(G);
j = 1..N(G))Î
[0,1]; j = 1..N(G)
(4.9)
2. Выполняются условия
g (G) = 1
Û g j(G)
= 1 для всех j = 1..N(G) (4.10)
и
g (G) > 0
Û g j(G)
> 0 для всех j = 1..N(G),
(4.11)
3. Справедлива зависимость
g j(G)
= 1 Û ç Μj1(G)
- Μj0(G)
ç < d
j(G) tj(G);
j = 1..N(G).
(4.12)
Согласно (4.7) и (4.9)
имеем
g (G) = 1
Û ç Μj1(G)
- Μj0(G)
ç < d
j(G) tj(G);
для всех j = 1..N(G)
(4.13)
Каков смысл зависимостей (4.8) - (4.13)?
Условие (4.10) будет выполняться, если
g (G) =
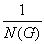
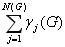 (4.14)
(4.14)
или
g (G) =
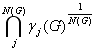 (4.15)
(4.15)
В том случае, когда величина
g (G)
определяется зависимостью (4.14) через суммы
величин
g j(G)
= 1; j = 1..N(G),
говорят, что величиной g (G)
организм человека характеризуется как суммативная система.
А если величина g
(G) определяется
зависимостью (4.15) через п р о и з в е де н
и я выше указанных величин, то говорят, что величиной g
(G) организм человека
характеризуется как ц е л о с т н а я с и с т е м а.
Если имеет место зависимость (4.14), то
необходимости выполнения условия (4.11) нет.
Однако, такая необходимость существует когда справедлива зависимость (4.15).
И что более важно, для того, чтобы выполнялось
условие (4.10), в первую очередь, всегда должно выполняться условие (4.11).
Таким образом, выполнение условия (4.11),
является одним из важнейщих признаков целостности
организма.
В целом совокупность зависимостей (4.10) и
(4.11) указывает на то, что величина g (G)
служит характеристикой о б щ е г о качества живого
организма и его функциональных частьей. Это качество является общим в том
смысле, что каждой функциональной частью организма оно проявляется
с о в м е с т н о и т о л ь к о с о в м е с
т н о со всеми остальными функциональными частями этого организма.
Качество, которое живым организмом и его
функциональными частями проявляется с о в м е с т н о и т о л ь к о с о в м е с
т н о, академиком В.Г. Афанасьевым было названо е д и н ы м и н т е г р а т и в
н ы м к а ч е с т в о м целостной системы.
Наличие единого интегративного качества (ЕИК),
согласно В.Г. Афанасьеву, является самым главным признаком целостности систем
[18 - 20].
Следует отметить, что еще раньше о наличии некого общего качества живого
организма и его физиологических систем указывал Г. Селье. Доказательством
наличия такого общего качества Селье видел в том, что в живом организме в
стрессовых ситуациях всегда виделяется одно и тоже вешество – адреналин
[21-22]..
Итак, величинами
g (G)
и g
j(G); j
= 1..N(G)
живой организм и его функциональные части характеризуются как целостные
системы.
В том случае, когда выполняется условие
ç Μj1 - Μj0
ç < d
j* t
j*,; для всех j
= 1..N(G), (4.16)
с доверительной вероятностью P »
1 утверждают,
что человек находится в нормальном состоянии.
Соответственно
в том случае, когда выполняется условие
ç Μj1(G)
- Μj0(G)
ç < d
j*(G)
t j*(G);
для всех j = 1..N(G)
(4.17)
с доверительной вероятностью P(G)
утверждают, что
человек находится в нормальном состоянии.
Согласно (4.6) имеет место
ç Μj1(G)
- Μj0(G)
ç < d
j(G)
t j(G)
Þ ç Μj1(G)
- Μj0(G)
ç < d
j*(G)
t j*(G)
(4.18)
Следовательно, в том случае, когда
ç Μj1(G)
- Μj0(G)
ç < d
j(G)
t j(G);
для всех j = 1..N(G),
(4.19)
всегда будет выполняться и условие (4.17).
Определение 6.
Пусть, в момент времени T
выполняется условие (4.17).
Тогда и только тогда с доверительной вероятностью P(G)
утверждают, что
в момент времени T человек находится в нормальном
состоянии в о б ы ч н о м смысле. А в том
случае, когда выполняется условие (4.19), говорят,
что в момент времени T
человек находится в нормальном состоянии в ш и р о к о м –
о б щ е с и с т е м н о м - смысле.
В итоге, смысл зависимости (4.13):-
человек находится в нормальном состоянии в широком – системном – смысле тогда и
только тогда, когда g (G) = 1.
Смысл зависимости (4.10):-организм как е
д и н о е ц е л о е существует, пока как
единые целые существуют все без исключения его функциональные части,
характеризуемые величинами
уj ;
j = j = 1..N(G).
В итоге, с точки зрения сохранения целостности
организма, все его части являются
р а в н о в а ж н ы м и. Отсюда, со своей
стороны, следует, что величины
g j(G)
; j = 1..N(G)
являются р а в н о в а ж н ы м и частными показателями наличия ЕИК
у функциональных частей организма, а величина
g (G)
является показателем наличия ЕИК
у самого организма, как единого целого. Что
касается зависимости (4.10), то она указывает на
то, что каждой функциональной частью организма ЕИК п о л н о с т ь
ю может быть проявлено только в том случае,
когда это качество будет проявлено полностью в с е м и
остальными функциональными частями организма.
Состояние,
когда ЕИК проявляется полностью всеми функциональными частями живого
организма, согласно (4.13),
и является нормальным состоянием этого организма в
широком – системном – смысле.
В итоге, смысл совокупности зависимостей
(4.10) и (4.11): величина g
(G) является
а н а л и т и ч е с к о й мерой нормальности состояния здоровья в с е г о
целостного организма, а каждая g
j(G)
представляет собой а н а л и т и ч е с к ую меру нормальности состояния
его j-ой функциональной
части.
В целом смысл совокупности зависимостей
(4.8), (4.10) и (4.13):
величина g (G)
является самой важной системной
характеристикой здоровья организма человека. А смысл совокупности зависимостей
(4.9), (4.11) и (4.12): -каждая величина
g j(G)
является
самой важной системной характеристикой здоровья j-ой
функциональной части организма человека.
Определение 7
Пусть, имеет место совокупность зависимостей 4.8
– 4.13.
Тогда и только тогда говорят, что
1. Величина g
(G) является а н а л и т и ч
е с к о й м е р о й б л и з о с т и
ф а к т и ч е с к о г о с о с т о я н и я ч е л о в е к а к е г о в о з м о ж
н о м у
н о р м а л ь н о м у с о с т о я н и ю.
2. Величина g
j(G)
является а н а л и т и ч е с к о й м е р о й б л и
з о с т и
ф а к т и ч е с к о г о с о с т о я н и я j –о й ф у н
к ц и о н а л ь н о й ч а с т и
о р г а н и з м а ч е л о в е к а к е е в о з м о ж н о м у н о р м а л ь н о
м у
с о с т о я н и ю.
В случае, когда человек болен, о величине
g (G)
также говорят, что она является
с т е п е н ь ю з д о р о в ь я больного человека.
Итак, величина g
(G), служащая
количественной характеристикой проявления единого интегративного качества живого
организма как целостной системы, одновременно является аналитической мерой
близости фактического состояния организма к его возможному нормальному
состоянию.
Далее мы будем полагать, что справедлива
зависимость
Y(O,G) =
Æ Û ç
Μj1(G) -
Μj0(G)
ç < d
j(G)
t j(G)
для всех j = 1..N(G),
(4.20)
а также и зависимость
g j(G)
Î [0,1] при j = 1..N(P,G)
и (4.21)
g j(G)
= 1 при j = N(P,G)
+ 1; …, N(G)
Согласно (4.21)
имеет место
N(O,G) =
0 Û g
j(G) = 1
для всех j = 1..N(G)
и, следовательно,
Y(O,G) =
Æ Û g
j(G) = 1
для всех j = 1..N(G)
(4.22)
5. Предельно- допустимые значения характеристик
состояния здоровья
Обозначим через ajmin(G)
и ajmax(G) значения
величины Μj1(G)
такие, что если
g j(G)
> 0, (5.1)
то
0 < d
j(G) tj(G)
£ ajmin(G)
£ bjl
1(G) £
ajmax(G)
< ¥
для всех l = 1..Nj1(G)
, (5.2)
т.е. вообще
g j(G)
> 0 Þ 0 <
d j(G)
t j(G)
£ ajmin(G)
£ bjl
1(G) £
ajmax(G)
< ¥
для всех l = 1..Nj1(G)
, (5.3)
где
bjl 1(G)
–значение bjl
1 такое, что
bjl = bjl
1(G) при P = P(G) (5.4)
Определение 8.
Пусть, в момент времени Т имеет место
(5.1) и, следовательно, согласно (5.3), выполнется условие (5.2).
Тогда и только тогда говорят, что в
момент времени T для
организма человека величины ajmin(G)
и ajmax(G)
соответственно являются м и н и м а л ь н о и
м а к с и м а л ь н о д о п у с т и м ы м
и з н а ч е н и я м и yj Î
Y в ш и р о к о
м
смысле.
Обозначим
aj(G) =
ajmin(G)
и dj(G)
= + 1 при Μj(G)
£ Μj0(G)
и (5.5)
aj(G) =
ajmax(G) и
dj(G) = - 1 при Μj1(G)
> Μj0(G)
Можно показать, что если g j(G)
> 0, то
ç Μj1(G)
- aj(G)
ç £ ç
Μj0(G) -
aj(G)
ç (5.6)
и
(Μj1(G) -
aj(G) )
dj(G) ³ 0 ,
(5.7)
В самом деле, пусть, g j(G)
> 0 и, следовательно, согласно (5.3),
выполняется условие (5.2). Тогда, согласно (2.4) и
(2.9), будет иметь место
ajmin(G)
£ Μj1(G)
£ ajmax(G)
(5.8)
Величина Μj0(G)
по определению является одной из допустимых
значений Μj1(G).
Следовательно, так же должно иметь место
ajmin(G)
£ Μj0(G)
£ ajmax(G)
(5.9)
Пусть, выполняется условие
Μj1(G)
£ Μj0(G)
Тогда из (5.8) и (5.9) получим
ajmin(G)
£ Μj0(G)
Отсюда и из (5.5)
получаем, что
ç Μj1(G)
- aj(G)
ç £ ç
Μj0(G) -
aj(G)
ç
и
(Μj1(G) -
aj(G) )
dj(G) ³ 0 ,
т.е. выполняется совокупность условий (5.6) и
(5.7).
Пусть, теперь выполняется условие
Μj1(G)
> Μj0(G)
Тогда из (5.8) и (5.9) получим
Μj0(G)
< Μj1(G)
£ ajmax(G)
Отсюда и из (5.5)
опять получаем, что
ç Μj1(G)
- aj(G)ç
£ ç Μj0(G)
- aj(G)ç
и
(Μj1(G) -
aj(G))
dj(G) ³ 0 ,
т.е. выполняется совокупность условий (5.6) и (5.7).
Итак
g j(G)
> 0 Þ ç Μj1(G)
- aj(G)
ç £ ç
Μj0(G) -
aj(G)ç
и (Μj1(G) -
aj(G))
dj(G) ³ 0
(5.10)
Можно показать, что
÷ Μj0(G)
- ajmin(G)ç
= ÷ Μj0(G)
- ajmax(G)ç
(5.11)
В самом деле, пусть, состояние здоровья человека
такое, что его организм друг от друга может различать только два возможных
значения величины yj: -
нормальное Μj0(G)
и предельно допустимое aj(G)
и, следовательно, имеет место
Nj1(G) =
2 (5.12)
С учетом (5.12) из (2.4)
и (2.10) получаем
Μj1(G) =
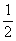 (bj11(G)
+ bj21(G)
) (5.13)
(bj11(G)
+ bj21(G)
) (5.13)
и
Sj2(G)
= 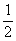 [(Μj1(G)
- bj11(G))2
+ (Μj1(G) -
bj21(G))2],
(5.14)
[(Μj1(G)
- bj11(G))2
+ (Μj1(G) -
bj21(G))2],
(5.14)
Величины bj11(G)
и bj21(G)
по определению являются друг отдруга различимими,
т.е. имеет место
bj11(G)
¹ bj21(G)
Для определенности положим, что
bj11(G)
< bj21(G)
(5.15)
Совокупность условий (5.5), (5.12) и (5.15)
будет выполняться, если положим, что
aj(G) =
ajmin(G) =
bj11(G)
при Nj1(G)
= 2 и Μj(G)
£ Μj0(G)
и
aj(G) =
ajmax(G) =
bj21(G)
при Nj1(G)
= 2 и Μj(G) > Μj0(G),
т.е. вообще имеет место
ajmin(G) =
bj11(G)
при Nj1(G)
= 2 и Μj1(G)
£ Μj0(G)
и (5.16)
ajmax(G) =
bj21(G)
при Nj1(G)
= 2 и Μj1(G) > Μj0(G)
Согласно (5.13) имеет место
bj21(G)
= 2 Μj1(G) -
bj11(G)
при Nj1(G)
= 2 (5.17)
Отсюда и из (5.14) имеем
Sj12(G)
= [Μj1(G) -
bj11(G)]2
(5.18)
Вообще,
согласно (2.12) имеет место
Sj1(G) >
0
С учетом этого из (5.18) получаем
Sj1(G) =
½ Μj1(G)
- bj11(G)½
при Nj1(G)
= 2 (5.19)
или, согласно (5.17),
Sj1(G) =
½ Μj1(G)
- bj21(G)½
при Nj1(G)
= 2 (5.20)
Согласно (5.19) и (5.20)
имеет место
½ Μj1(G)
- bj11(G)½
= ½ Μj1(G)
- bj21(G)½
при Nj1(G)
= 2 (5.21)
В том случае, когда Nj1(G)
= 2, величина yj,
как указывалось выше, имеет два возможных значения
Μj0(G)
и aj(G),
т.е. имеет место
Μj1(G) = Μj0(G)
при Nj1(G)
= 2 (5.22)
С учетом (5.22) из (5.21) получаем
½ Μj0(G)
- bj11(G)½
= ½ Μj0(G)
- bj21(G)½
при Nj1(G)
= 2
Отсюда и из (5.16) имеем
½ Μj0(G)
- ajmin(G)ç
= ÷ Μj0(G)
- ajmax(G)½
,
т.е. получаем (5.11).
Пусть, ajmin(L,G))
и ajmax(L,G))
- значения величины yj
Î Y такие, что
ajmin(L,G)
= d j(G) t
j(G) и
ajmax(L,G)
= 2 Μj0(G)-
d j(G)
t j(G) (5.23)
Согласно (5.2) и (5.23)
имеют место
0 < ajmin(L,G)
£ ajmin(G)
и ajmax(G)
£ ajmax(L,G)
(5.24)
Вообще, согласно (4.3), (4.4)
и (4.6) каждая пара
< d j(G), t
j(G) > ; j =
j0; j0 = 1..N
содержит в себе сведения об одной, вполне
определенной – конкретной, локальной - функциональной части организма человека.
Принимая во внимание это, о величинах ajmin(L,G)
и ajmax(G)
можно говорить, что для организма человека эти
величины в момент времени Т соответственно являются м и н и м а л ь н о
и м а к
с и м а л ь н о допустимыми значениями величины yj
Î Y в у з к о м – л ок а л ь н о м – смысле.
Пусть, Sjmax(L,G)
- значение Sj1(G)
такое, что
Sjmax(L,G)
= ç Μj0(G)
- aj(L,G)
ç , (5.25)
где
aj(L,G))
= ajmin(L,G)
при Μj1(G)
£ Μj0(G)
и (5.26)
aj(L,G))
= ajmax(L,G)
при Μj1(G)
> Μj0(G)
Можно показать, что вообще
Sj1(G)
£ Sjmax(L,G)
при g j(G)
> 0 (5.27)
и при этом
Sj1(G) =
Sjmax(L,G)
Û Nj1(G)
= 2 и bj11(G)=
aj(L,G)
(5.28)
В самом деле, согласно (5.3), (5.23) и
(5.24), имеет место
g j(G)
> 0 Þ ajmin(L,G)
£ bj11(G)
£ ajmax(L,G)
для всех l = 1..Nj1(G)
С учетом этого из (5.6), (5.19) и (5.26) имеем
Sj1(G)
£ ½ Μj1(G)
- aj(L,G)
½ £ ½
Μj0(G)-
aj(L,G)
½ (5.29)
и, в конечном счете, согласно (5.25),
Sj1(G) £ Sjmax(L,G),
т.е. получаем (5.27).
Кроме этого, согласно (5.19) и (5.25), имеет место
Sj1(G)
= Sjmax(L,G)
при bj11(G)
= aj(L,G)
Но сама зависимость (5.19), согласно (2.4) и
(2.10), справедлива в том и только в
том случае, когда выполняется условие (5.12).
Следовательно, вообще имеет место
Sj1(G) =
Sjmax(L,G)
Û Nj1(G)
= 2 и bj11(G)=
aj(L,G),
т.е. получаем (5.28).
Как видно, условие (5.27)
выполняется благодаря тому, что имеет место
(5.29), т.е. вообще
Sj1(G)£
Sjmax(L,G)
при ajmin(L,G)£
bj11(G)£
ajmax(L,G)
для всех l = 1..Nj1(G)
(5.30)
Принимая во внимание зависимость (5.30),
о величине Sjmax(L,G)
можно говорить, что в момент времени Т для
организма человека эта величина является м а к с и м а л ь н о
д о п у с т и м ы м
значением Sj1(G)
в л о к а л ь н о м
смысле..
Пусть
d jmin (G),
t jmin(G),
d jmax(G)
и t jmax(G)
- значения d
j(G) и
t j(G)
такие, что
d j(G)
= d jmin(G)
и t j(G)
= t jmin(G)
при Sj1(G)
= Sj0(G)
и Nj1(G)
= Nj0(G)
и (5.31)
d j(G)
= d jmax(G)
и t j(G)
= t jmax(G)
при Sj1(G) =
Sjmax(L,G)
и Nj1(G) = 2
Согласно (4.5), , (4.7), (5.27) и (5.31) имеет место
0 < d jmin(G)
t jmin(G)
= d j0(G)
t j0(G)
£ d j(G)
t j(G)
£ d
jmax(G) t
jmax(G) (5.32)
где
d jmin(G)
= Sj0(G)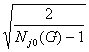 и t jmin(G)
= t j(P(G),
2(Nj0(G)
–1)) (5.33)
и t jmin(G)
= t j(P(G),
2(Nj0(G)
–1)) (5.33)
d jmax(G) =
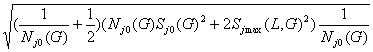 и
t jmax(G) =
и
t jmax(G) =
= t j(P(G), Nj0(G))
(5.34)
Обозначим через ajmin(Z,G)
и ajmax(Z,G) значения ajmin(G)
и ajmax(G) такие,
что
ajmin(G) = ajmin(Z,G) и ajmax(G)
= ajmax(Z,G)
при ç Μj1(G)
- Μj0(G) ç
< d jmin(G)
t imin(G) (5.35)
Определение 9
Пусть
0 < ajmin(Z,G) £
ajmin(G) £ Mj1(G)
£ ajmax(G) £ ajmax(Z,G).
(5.36)
и при этом
существует величина Sjmax(Z,G)
такая, что
Sjmax(G) = Sjmax(Z,G) при
ç Μj1G) - Μj0(G)
ç < d
jmin(G) t imin(G)
и (5.37)
Sjmax(G) < Sjmax(Z,G)
при ç Μj1G)
- Μj0(G) ç
³ d jmin(G)
t imin(G)
т.е. вообще
Sjmax(G) ≤ Sjmax(Z,G). (5.38)
Тогда и только тогда говорят, что величина Sjmax(Z,G)
является м а к с и м а л ь н о
д о п у с т и м ы м значением Sj1
для организма з д о р о г о г о
человека.
Говорят также, что Sjmax(Z,G)
является максимально допустимым значением
Sj1
для организма человека в с и с т е м н о м –
ш и р о к о м – смысле.
Как видно, величина Sjmax(Z,G)
является характеристикой з д о р о в о г о
человека и, следовательно, она не зависит от его фактического состояния.
Согласно (5.25) и (5.36)
имеет место
Sjmax(Z,G) =
ç Μj0(G)
- aj(Z,G)
ç ; j = 1..N(G)
, (5.39)
где
aj(Z,G) =
ajmin(Z,G)
при Μj1(G)
£ Μj0(G)
и (5.40)
aj(Z,G) =
ajmax(Z,G) при Μj1(G)
> Μj0(G)
Так как,
согласно (5.36) и (5.40), вообще
aj(Z,G)
> 0; j = 1..N(G),
из (5.39) имеем
Sjmax(Z,G)
< Μj0(G)
и, в конечном счете, согласно (5.30) и (5.38),
Sj1(G)
£ Sjmax(L,G)
£ Sjmax(Z,G)
< Μj0(G);
j = 1..N(G)
(5.41)
6. Определение предельно-допустимых значений
первичных показателей
состояния здоровья человека
Обозначим
a j(G)
= 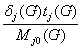 и a
j(Z,G)
= a jmin(G),
(6.1)
и a
j(Z,G)
= a jmin(G),
(6.1)
где
a jmin(G)
= 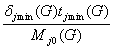 (6.2)
(6.2)
Согласно (5.2), (5.32), (6.1) и (6.2) имеет место
0 < a j(Z,G)
£ a j(G)
< 1; j = 1..N(G)}
(6.3)
и, следовательно,
0 < a (Z,G)
£ a (G)
) < 1, (6.4)
где
a (G) = max{a
j(G); j
= 1..N(G)}
и (6.5)
a (Z,G)
= min{a j(Z,G);
j = 1..N(G)}
Обозначим
Cj(G) = ç
1 -  ç
, если a (G) ≤
ç 1 -
ç
, если a (G) ≤
ç 1 -
 ç
< 1
ç
< 1
Cj(G) =
ç 1 -
 ç
, если a (G) ≤
ç 1 -
ç
, если a (G) ≤
ç 1 -
 ç
< 1
ç
< 1
Cj(G) = c
1 - Mj1(G) /
Mj0(G)
c , если
a (G) ≤
c 1- Mj1(G)
/ Mj0(G)
c ≤ c 1- aj(G)
/ Mj0(G)
c
Cj(G) = 0 ,
если c 1 -
Mj1(G) /
Mj0(G)
c > c 1 -
aj(G) / Mj0(G)
c (6.6)
Cj(G) = 1 - a
(G)), если
c 1 - Mj1(G)
/ Mj0(G)c
< a (G)
C(G) = max{Cj(G);
j = 1..N(G)}
(6.7)
Согласно (6.5) имеет место
a (G) ³
a j(G)
> 0; j = 1..N(G)
(6.8)
и, следовательно,
ç Μj1(G)
- Μj0(G)
ç ³ a
(G) Mj0(G)
Þ ç Μj1(G)
- Μj0(G)
ç ³ a
j(G) Mj0(G)
(6.9)
Ввиду этого в том случае, когда выполняется услоие (5.1), можно полагать, что
0 < a j(G)
≤ a (G) ≤ Cj(G)
≤ C(G) ≤ C(Z,G)
при ç Μj1(G)
- Μj0(G)
ç ³ a
(G) Mj0(G)
и (6.10)
0 < a j(G)
≤ a (G) ≤ Cj(G)
= C(G) = C(Z,G)
при ç Μj(G)
- Μj0(G)
ç < a
(G) Mj0(G),
т.е. вообще
0 < a j(G)
≤ a (G) ≤ Cj(G)
≤ C(G) ≤ C(Z,G),
(6.11)
где
C(Z,G) –значение
C(G)
такое, что
C(G) = C(Z,G)
при ç Μj1(G)
- Μj0(G)
ç < a
j(G) Mj0(G)
(6.12)
Согласно (5.2), (5.9), (5.36) и (5.40) имеет
место
ç Μj0(G)
- Μj1(G)
ç ≤ ç Μj0(G)
- aj(G)
ç ≤ ç Μj0(G)
- aj(Z,G)
ç
или
ç 1 -
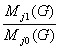 ç
≤ ç 1 -
ç
≤ ç 1 -
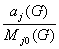 ç
≤ ç 1 -
ç
≤ ç 1 -
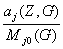 ç
(6.13)
ç
(6.13)
Отсюда и из (6.6) имеем
Cj(G) ≤
ç 1 -
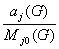 ç
≤ ç 1 -
ç
≤ ç 1 -
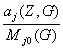 ç
(6.14)
ç
(6.14)
Условия (6.7), (6.11), (6.12) и (6.14) будут
выполняться, если положим, что вообще
C(G) = ç
1 - 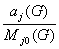 ç
и C(Z,G)
= ç 1 -
ç
и C(Z,G)
= ç 1 -
 ç
(6.15)
ç
(6.15)
Из (5.5) и(6.15) получаем
aj(G) = (1 – С(G)
dj(G)) Μj0(G)
и aj(Z,G)
= (1 – С(Z,G) dj(G)
) Μj0(G), (6.16)
Согласно (5.5), (5.40) и (6.16) имеет место
÷ Μj0(G)
- ajmin(G)ç
= ÷ Μj0(G)
- ajmax(G)ç
и (6.17)
÷ Μj0(G)
- ajmin(Z,G)ç
= ÷ Μj0(G)
- ajmax(Z,G)ç
Как видно, величина Μj0(G)
всегда является р а в н о у д а л е н н о й
от предельно допустимых значений Μj1(G).
Обозначим
D j(G)
= a (G)
Mj0(G). (6.18)
Согласно (6.1), (6.5) и (6.18) имеет место
D j(G)
³ d j(G)
tj(G)
Следовательно, условие (5.2) будет выполняться,
если положим, что
ajmin(G) =
D j(G)
(6.19)
Отсюда и из (6.17) имеем
ajmax(G) = 2 Μj0(G)
- D j(G) (6.20)
В итоге, из (5.5), (6.19) и (6.20) получаем
aj(G) =
D j(G)
при Μj1(G)
≤ Μj0(G)
и (6.21)
aj(G) = 2 Μj0(G)
- D j(G)
при Μj1(G)
> Μj0(G)
и, в конечном счете, согласно (6.4), (6.15) и (6.18),
a (G) + C(G)
= 1 (6.22)
Согласно (6.22) имеет место
a (G) = 1 -
a (G), (6.23)
А согласно (6.11)имеем
0 < a (G) ≤
C(G) (6.24)
Из (6.23) и (6.24) получаем
0 < a (G) ≤ 1 -
a (G)
Отсюда
0 < a (G) ≤ 0.5
и, следовательно, согласно (6.22), вообще
0 < a (G) ≤ 0.5
и 0.5 ≤ C(G)
< 1 (6.25)
Можно показать, что
a (Z,G)
+ C(Z,G) =
1
0 < a (Z,G)
≤ a (G) ≤ 0.5
и 0.5 ≤ C(G)
≤ C(Z,G) <
1 (6.26)
0 < D j(Z,G)
≤ D j(G)
≤ Mj1(G) ≤
(2 Mj0(G) -D
j(G)) ≤ (2
Mj0(G) -
D j(G)),
где
D j(Z,G)
= a (Z,G)
Mj0(G).
(6.27)
Определение 10
Пусть, имеет место (5.1) и при этом выполняются
условия (6.22), (6.25) и (6.26).
Тогда и только тогда говорят, что справедлива зависимость
g j(G)>0
Û 0 j(Z,G)≤D
j(G)≤Mj1(G)≤(2
Mj0(G)-D
j(G))≤(2
Mj0(G)-D
j(Z,G))
(6.28)
7.Аналитическая мера близости фактических
состояний функциональных частей
организма к их нормальным состояниям
Пусть, mj(G)
и mj(Z,G)
–натуральные числа такие, что
mj(G) =
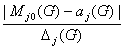 + 2 и mj(Z,G)
=
+ 2 и mj(Z,G)
= 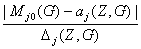 + 2 (7.1)
+ 2 (7.1)
Через mj(G),
как видно, обозначено количество значений
величины yj ,
отдаленных друг от друга на расстояние
D j(G).
При этом все эти значения принадлежат
области [ajmin(G)
, ajmax(G)].
Можно показать, что
mj(G) = m(G)
для всех j = 1..N(G)
и (7.2)
mj(Z,G) = m(Z,G)
для всех j = 1..N(G)
где
m(G) = 1 + (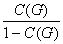 )
и m(Z,G) =
1 + (
)
и m(Z,G) =
1 + (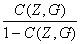 ) (7.3)
) (7.3)
В самом деле, согласно (6.16), (6.18) и (7.1),
имеет место
mj(G) = (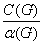 )
+ 2,
)
+ 2,
а согласно (6.16), (6.27) и (7.1) имеем
mj(Z,G) = (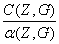 )
+ 2
)
+ 2
Отсюда и из (6.18) и (6.22) имеем
mj(G) = (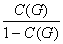 )
+ 2 и mj(Z,G)
= (
)
+ 2 и mj(Z,G)
= ( ) + 2
) + 2
и, в конечном счете, согласно (7.3),
mj(G) = m(G)
для всех j = 1..N(G)
и
mj(Z,G) = m(Z,G)
для всех j = 1..N(G),
т.е. получаем (7.2).
Согласно (7.1) и (7.2) имеет место
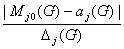 = m(G)
– 2 для всех j = 1..N(G)
= m(G)
– 2 для всех j = 1..N(G)
и (7.4)
 = m(Z,G)
– 2 для всех j = 1..N(G)
= m(Z,G)
– 2 для всех j = 1..N(G)
Свойство живого организма, выраженное
зависимостью
mj(G) = m(G)
для всех j = 1..N(G),
нами было установлено в 1983 году. В последствии это свойство мы назвали
закономерностью сохранения количества воспринимаемых значений [23].
Согласно (6.26) имеет место
C(G) ≤ C(Z,G)
С учетом этого из (7.3) получаем
m(G) ≤ m(Z,G)
< ¥
Далее, согласно (6.26) имеет место
0.5 ≤ C(G) < 1
С учетом этого из (7.3) получаем
m(G) = 3, 4, 5, ..,
m(Z,G) <
¥ (7.5)
Как видно, каждый первичный показатель состояния
здоровья живого организма имеет т р и и б о л е е возможных воспринимаемых
значений.
Обозначим
Dj(G) = Round(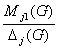 )
D j(G) и Dj(Z,G)
= Round(
)
D j(G) и Dj(Z,G)
= Round(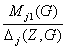 )
D j(Z,G) (7.6)
)
D j(Z,G) (7.6)
Согласно (6.28) и (7.6) имеет место
g j(G)
> 0 Û 0 < D
j(G) ≤
Dj1(G) ≤ (2
Mj0(G) -
D j(G)) (7.7)
А согласно (5.6), (5.7) и (7.6) имеем
ç Dj1(G)
- aj(G)
ç £ ç
Μj0(G) -
aj(G)
ç
и (7.8)
(Dj1(G) - aj(G) ) dj(G)
³ 0 ,
При этом, согласно (5.10) и (7.7) выполняется условие
g j(G)
> 0 Þ ç Dj(G)
- aj(G)
ç £ ç
Μj0(G) –
- aj(G)
ç и (Dj(G)
- aj(G) )
dj(G)
³ 0 (7.9)
Обозначим
b i(G)
= 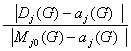 b j1(G),
если ç Dj1(G)
–
b j1(G),
если ç Dj1(G)
–
- aj(G)
ç b j1(G)
≤ ç Μj0(G)
- aj(G)
ç
и (7.10)
b i(G)
= 0, если ç Dj1(G)
- aj(G)
ç b j1(G)
> ç Μj0(G)
- aj(G)
ç ,
где
b j1(G)
= 1, если (Dj1(G)
- aj(G) )
dj(G)
³ 0
и (7.11)
b j1(G)
= 0, если (Dj1(G)
- aj(G) )
dj(G) < 0
Можно показать, что совокупность условий (4.9) и (4.12) будет выполняться,
если положим, что вообще
g I(G)
=
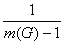 ((m(G) - 2 ) b
j(G) + 1) (7.12)
((m(G) - 2 ) b
j(G) + 1) (7.12)
В самом деле, согласно (2.4), (2.10), (4.3), (4.4) ), (4.5) ), (6.6) и (6.7),
имеет место
C(G) = f(Μj1(G),
Sj1(G),
Nj1(G), Μj0(G),
Sj0(G),
Nj0(G));
j = 1..N(G))
Отсюда и из (7.3) имеем
m(G) = f(Μj1(G),
Sj1(G),
Nj1(G),
Μj0(G),
Sj0(G),
Nj0(G));
j = 1..N(G))
и, в конечном счете, согласно (7.12),
g I(G)
= fj(Μj1(G),
Sj1(G),
Nj1(G),
Μj0(G),
Sj0(G),
Nj0(G));
j = 1..N(G)),
т.е. выполняется условие (4.9).
Величины
a j(G)
и a j(Z,G);
j = 1..N(G)
являются объективными характериситиками целостого организма. Следовательно,
справедливость неравенства (6.3) является не случайностью, а з а к о н о м е р н
ы м следствием стремления целостного организма обеспечить выполнение условия
a j(G) =
a min(G); j = 1..N(G), (7.13)
где
a min(G)
–минимально–возможное значение величины
a j(G),
объективно обусловленное внешними и внутренними
условиями существования целостного организма: a
min(G) > 0.
Условие (7.13), согласно (6.3), наилучшим
образом выполняется в т о м и т о л ь к о в т о м с л у ч а е, к о г д а о р г а
н и з м н а х о д и т с я в н о р м а л ь н о м
с о с т о я н и и. Следовательно, когда имеет место
a j(G)
= a j(Z,G)
= a min(G)
для всех j = 1..N(G),
(7.14)
можно говорить, что состояние организма является нормальным в самом ш и р о к
о м смысле.
Определение 11
Пусть, имеет место (7.14).
Тогда и только тогда говорят, что организм
человека находится в н о р м а л ь н о м
с о с т о я н и и в с а м о м ш и р о к о м – с и с т е м н о м – с м ы с л
е.
Согласно (7.6) и (7.14) имеет место
ç Μj0(G)
- Mj1(G)
ç = 0 Þ
ç Μj0(G)
- Mj1(G)ç
< a j(Z,G)
Μj0(G), (7.15)
С учетом (7.15) из (6.1), (6.2) и (7.11)
находим
ç Μj0(G)
- Dj1(G)
ç = 0 Þ
ç Μj0(G)
- Mj1(G)ç
< a j(Z,G)
Μj0(G)
ç ≤ a
j(G) Μj0(G)
(7.16)
Отсюда и из (5.32), (6.1) и (7.11) имеем
b i(G)
= 1 при ç Μj0(G)
- Mj1(G)ç
< a j(G)
Μj0(G)
и, в конечном счете, согласно (6.1) и (7.12),
g i(G) = 1 при
ç Μj0(G) - Mj1(G)ç
< d j(G) tj(G) (7.17)
Покажем, что также имеет место
ç Μj0(G)
- Mj1(G)ç
< a j(G)
Μj0(G)
при g
i(G) = 1
В самом деле, пусть, имеет место
g i(G)
= 1
и, следовательно, выполняется условие
g j(G)
> 0 (7.18)
С учетом (7.18) из (7.9) получаем
ç Dj1(G)
- aj(G)
ç £ ç
Μj0(G) -
aj(G)ç
(7.19)
и
(Dj1(G) - aj(G)) dj(G) ³
0 (7.20)
Отсюда и из (7.10) и (7.19) получаем
b i1(G)
= 1 при ç Μj0(G)
- Dj1(G)ç
= 0 (7.21)
А вообще, согласно (7.12), имеет место
b i(G)
= 1 Û g
i(G) = 1
Отсюда и из (7.21) имеем
ç Μj0(G)
- Dj1(G)ç
= 0 при g i(G)
= 1
и, в конечном счете, согласно (7.15),
ç Μj0(G)
- Mj1(G)ç
< a j(G)
Μj0(G) (7.22)
В итоге, из (6.1), (7.17) и (7.22) имеем
g i(G)
= 1 Û ç Μj0(G)
- Mj1(G)ç
< d j(G)
t j(G),
т.е. получаем (4.12).
Обозначим
b i(Z,G)
=  b j1(Z,G),
если ç Dj1(Z,G)
–
b j1(Z,G),
если ç Dj1(Z,G)
–
- aj(Z,G)
ç b j1(Z,G)
≤ ç Μj0(G)
- aj(Z,G)ç
и (7.23)
b i(Z,G)
= 0, если ç
Dj1(Z,G)
- aj(Z,G)ç
b j1(Z,G)
> ç Μj0(G)
- aj(Z,G)ç
,
где
b j1(Z,G)
= 1, если (Dj1(Z,G)
- aj(Z,G))
dj(G)
³ 0
и (7.24)
b j1(Z,G)
= 0, если (Dj1(Z,G)
- aj(Z,G))
dj(G) < 0
Можно проверить, что вообще
g I(G)
³ g
I(Z,G), (7.25)
где
g I(Z,G) =
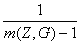 ((m(Z,G) - 2 )
b j(Z,G) + 1) (7.26)
((m(Z,G) - 2 )
b j(Z,G) + 1) (7.26)
При этом, согласно (7.12) и (7.25), имеет место
g I(G) =
g I(Z,G) = g
Imin(G) = g Imin(Z,G)
при b i(G) =
b i(Z,G) = 0
или, с учетом
(7.10),
g I(G) = g
I(Z,G) = g Imin(G) =
g Imin(Z,G)
при ç Dj1(Z,G) -
aj(Z,G) ç b
j1(Z,G) > ç Μj0(G)
- aj(Z,G)ç (7.27)
где
g Imin(G)
=  и
g Imin(Z,G)
=
и
g Imin(Z,G)
= 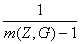 (7.28)
(7.28)
Из (6.21), (7.10) и (7.23) имеем
g I(G)
= g Imin(G)
при Dj1(G)
= ajmin(G)
или Dj1(G)
= ajmax(G),
т.е. g I(G)
является минимально возможным в том случае, когда величина yj
принимает предельно допустимое значение, что вполне логично.
При этом, соглано (7.24), имеет место
g Imin(G)
= 0 Û m(G)
= m(Z,G) =
¥
или, с учетом (6.22) и (6.26),
g Imin(G)
= 0 Û C(G)
= C(Z,G) =
1
Отсюда и из (6.26) имеем
g Imin(G)
> 0.
В итоге, в живом организме всегда имеет место
g I(G)
³ g Imin(G) > 0
при 0 < D j(G) ≤ Dj1(G)
≤ (2 Mj0(G) - D j(G)) (7.29)
8. Стратегические и тактические цели
функциональных частей
живого организма
Реализация события
b i(G)
= 1, (8.1)
согласно (7.10), зависит от значений д в у х величин. Ими являются величины
Dj(G)
и aj(G).
По этой причине, событие, выраженное зависимостью
(8.1), является сопоставимым с событием, выраженным зависимостью
b i(G)
= 1; i ¹ j
(8.2)
лишь в некотором у з к о м смысле.
Дело в том, что в ш и р о к о м смысле взаимосопоставимыми являются только
такие события, которые отличаются друг от друга только о д н и м единственным
признаком [24]. А события (8.1) и (8.2) друг от
друга различаются сразу двумя признаками: - фактическим и предельным значениями
соответствующих величин.
В отличие от событий (8.1) и (8.2), события
b i(Z,G)
= 1 и b
i(Z,G)
= 1 (8.3)
являются между собой взаимосопоставимыми в самом широком смысле.
Дело в том, что, как указывалось выше, для
организма человека величины
aj(Z,G);
j= 1..N(G)
являются вполне определенными. А точнее, эти величины н е з а в и с я т от
фактического состояния организма человека. Благодаря этому ширина каждой области
ç Μj1(G)
- aj(Z,G)
ç ; j = j0;
j0 = 1..N(G)
в каждый момент времени однозначно определяятся о д н и м единственным
признаком –ф а к т и ч е с к и м значением величины yj
, т.е. величиной Μj1(G).
Ввиду этого одним единственным признаком - фактическим значением - друг от друга
различаются и собыитя (8.3), т.е. эти события являются в з а и м о с о п о с т а
в и м ы м и
с о б ы т и я м и в с а м о м ш и р о к о м смысле.
Благодаря тому, что события (8.3) являются
взаимосопоставимыми в широком смысле, согласно (7.26), взаимосопоставимыми в
широком смысле являются и события
g j(Z,G) = 1 и
g i(Z,G) = 1; j,i = 1..N(G), (8.4)
Определение 12
Пусть, события (8.4) являются
взаимосопоставимыми в широком смысле и, следовательно, величины
g j(Z,G);
j = 1..N(G)
(8.5)
обозначают понянтия, которые друг от друга отличаются лишь о д н и м
единственным признаком.
Пусть, при этом признак, которым эти величины
друг от друга отличаются, в момент времени T
таков, что каждое событие
g i(Z,G)
= 1; j = j0 ;
j0 = 1..N(G)
реализуется тогда и только тогда, когда реализуются все без исключения
события
g j(Z,G)
= 1; j = 1..N(G):
Тогда и только тогда говорят, что в момент времени T:
1. Величины (8.5)
являются а г р е г и р у е м ы м и в ш и р о к о м
смысле.
2. Величины
g j(G)
= 1; j = 1..N(G)
(8.6)
являются а г р е г и р у е м ы м и в у з к о м смысле.
3. Цели
g i(Z,G) ®
1; j = 1..N(G) (8.7)
являются с т р а т е г и ч е с к и м и ц е л я м и функциональных частей
живого организма.
4. Цели
g i(G)
® 1; j = 1..N(G)
(8.8)
являются т а к т и ч е с к и м и ц е л я м и функциональных частей живого
организма.
Как видно, тактические цели организма строго
привязаны к его стратегическим целям: каждая цель
g i(G)
® 1; j = j0
; j0 = 1..N(G)
в качестве тактической цели j –ой
функциональной части организма может служить в том и только в том случае, когда
цель
g i(Z,G)
® 1; j = j0
; j0 = 1..N(G)
является стратегической целью j –ой
функциональной части организма.
О стратегических целях функциональных частей
живого организма также говорят, что в момент времени T
они составляют г е н е р а л ь н у ю совокупность
р а в н о в а ж н ы х п о д ц е л е й о б щ е й с т р а т е г и ч е с к о й ц
е л и живого организма. А о тактических целях функциональных частей живого
организма говорят, что в момент времени T
они составляют г е н е р а л ь н у ю совокупность
р а в н о в а ж н ы х п о д ц е л е й о б щ е й т а к т и ч е с к о й ц е л и
живого организма.
9. Теория П.К. Анохина и аналитическая мера
близости фактического состояния
организма к его возможному нормальному
состоянию.
По теории П.К.Анохина [25 - 27]
за получение « ж е л а е м о г о к о н е ч н
о г о
р е з у л ь т а т а » в каждый момент времени Т в организме человека
ответственность
несет в п о л н е о п р е д е л е н н а я
функциональная система S(T,G).
Следовательно, для того, чтобы организм мог
существовать и продольжать двигаться к «желаемому конечному результату», в
момент времени T
должны выполняться следующие условия
yj Î
Y(T,G)
Û 0 < g
j(T,G) < 1;
j =1..N(T,G),
(9.1)
и
0 < g j(T,G)
< 1 для всех j =1..N(T,G),
(9.2)
где
Y(T,G) -
совокупность функций, выполняемых системой S(T,G);
g j(T,G)
– значение g j(G)
в момент времени T:
g i(T,G) =
g i(G) при T = T0
; j = j0; j0 = 1..N(T0,G); (9.3)
T0 – некоторое фиксированное
значение T;
N(T,G) –объем
Y(T,G).
В самом деле, для организма живого
человека, как было показано выше, всегда имеет место:
g i(G)
³ g
imin(G) > 0;
для всех j =1..N(T,G),
Следовательно, если существует хоть одна величина g
i(T,G)
такая, что имеет место
g i(T,G)
= 0,
то это означает, что система S(T,G)
принадлежит организму м е р т в о г о человека.
Такая система, разумеется, не может нести какой- либо ответственности.
Таким образом, выполнение условия
0 < g j(T,G)
для всех j =1..N(T,G)
необходимо для того, чтобы система S(T,G)
смогла справиться со стоящей перед ней задачей:
выполнять все без исключения функции
yj Î
Y(T,G);
j =1..N(T,G).
Что касается условия
g j(T,G)
≤ 1 для всех j =1..N(T,G),
то необходимость его выполнения обусловлена необходимостью существования
целей
g i(G)
® 1; j = 1..N(T,G)
(9.4)
Дело в том, что если выполняется условие
Вер{g i(T,G)
= 1} = 1 при T = T0;
j = j0;
j0 = 1..N(T0,G),
то это указывает на то, что функциональная часть организма, характеризуемая
величиной yj, в
момент времени T0
находится в нормальном состоянии и, следовательно,
она не выполняет никакой работы. Для того, чтобы эта функциональная часть не
находилась в покое, а выполняла работу, в первую очередь, должна существовать
необходимость выполнения этой работы, т.е. должна существовать цель
g i(T,G)
® 1 при T = T0; j =
j0; j0 = 1..N(T0,G).
А такая цель может существовать только в том случае, когда вероятность
выполнения условия g i(G)
= 1 является меньшей 1 и, следовательно, имеет
место
0 < g i(G) ≤ 1
при T = T0; j = j0; j0 = 1..N(T0,G),
Система S(T,G),
как указывалось выше, сможет справиться со стоящей
перед ней задачей лишь в том случае, если будут выполнены все функций
yj Î
Y(T,G);
j =1..N(T,G).
Ввиду этого цели (9.4) и являются
равноважными подцелями общей тактической цели
g (T,G)
® 1,
стояшей в момент времени T
перед системой S(T,G).
В итоге, смысл совокупности зависимостей (9.1) и
(9.2): их справедливость является необходимым и достаточным условием для того,
чтобы система S(T,G)
cмогла справиться со стоящей перед ней задачей.
Обозначим
m(T,G) =
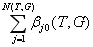 ; (9.5)
; (9.5)
и
g (T,G)
=  , (9.6)
, (9.6)
где
b j0(T,G)
= 1, если yj
Î Y(T,G)
и (9.7)
b j0(T,G)
= 0, если yj
Ï Y(T,G)
Можно показать, что
g (G) =
g (T,G)
при T =
T0 (9.8)
В самом деле, для совокупности величин
Y(T,G)
имеет место зависимость (9.2). Но эта совокупность
является г е н е р а л ь н о й совокупностью первичных показателей системы
S(T,G).
Следовательно, для всех остальных функциональных
частей организма должно иметь место
g j(T,G)
= 1; j = N(T,G)
+1, N(T,G)
+2,..,N(G) (9.9)
Отсюда и из (9.2) и (9.7) имеем
b j0(T,G)
= 0; j = N(T,G)
+1, N(T,G)
+2,..,N(G) (9.10)
С учетом (9.10) из (9.5) имеем
m(T,G) =
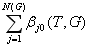 = N(T,G)
> 0 (9.11)
= N(T,G)
> 0 (9.11)
Согласно (9.9), (9.10) и (9.11) имеет место
 =
=
 (9.12)
(9.12)
Отсюда и из (9.6) имеем
g (T,G)
= 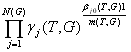 (9.13)
(9.13)
Согласно (9.3) и (9.13) имеет место
g (T,G)
= 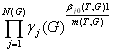 при T
= T0 (9.14)
при T
= T0 (9.14)
С учетом (4.9) из (9.11) и (9.14) получаем
g (T,G)
= f(Μjk(G),
Sjk(G),
Njk(G); k = 0,1;
j = 1..N(G))Î
[0,1] при T =
T0
g (T,G)
= 1 Û T = T0
и 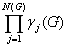 = 1 (9.15)
= 1 (9.15)
g (T,G)
> 0 Û T = T0
и 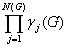 > 0
> 0
Сопоставляя совокупность зависимостей (9.15)
с совокупностью зависимостей (4.9), (4.10) и
(4.11), заключаем
g (G) =
g (T,G)
при T =
T0 ,
т.е. получаем (9.8).
Согласно (9.6) и (9.11) имеет место
g (T,G)
= 1, если g
j(T,G)
= 1 для всех N(G)
Отсюда смысл той части зависимости (9.6), где выполняется условие
g (T,G)
= 1, если m(T,G)
= 0.
Эта зависимость указывает на то, что в момент времени T
все части организма человека, включая систему
S(T,G),
находятся в нормальном состоянии.
Итак, для того, чтобы в момент времени
T установить, насколько состояние здоровья человека
близко к нормальному, необходимо и достаточно определить состояние той
функциональной части организма S(T,G),
для которой в этот момент времени имеет место:
0 < g j(G)
< 1; j =1..N(T,G);
N(T,G)
³ 1 (9.16)
Это именно та часть, которая в этот момент времени несет ответственность за
получение «желаемого конечного результата». Если окажется, что условие (9.16) не
выполняется, а точнее имеет место N(T,G)
= 0, то это означает, что весь организм находится в
нормальном состоянии.
Система S(T,G)
не всегда является известной. Следовательно, не всегда будет известной и
совокупность Y(T,G).
Можно проверить, что
Y(T,G) =
Y(O,G) при
T = T0 (9.17)
В самом деле, по определению Y(O,G)
имеет место
yj Î
Y(O,G)
Û Вер{g
j(G) < 1} > 0,
т.е. вообще
yj Î
Y(O,G)
Û g j(G)
≤ 1 (9.18)
Отсюда и из (9.1) имеем
Y(T,G) =
Y(O,G) при
T = T0 ,
т.е. получаем (9.17).
Следовательно,
N(T,G) =
N(O,G);
g (T,G)
= g ( (O,G);
g j(T,G)
= g j(
O,G) и b
j0(T,G)
= b j0(
O,G)
при T = T0, (9.19)
где
g (T,G)
= g ( (O,G);
g j(T,G)
= g j(
O,G) и b
j0(T,G)
= b j0(
O,G)
при Y(T,G)
= Y(O,G)
Согласно (9.10) и (9.19) имеет место
N(T,G) =
N(O,G) =
N при
Y(O,G)
Í YÍ Y(G),
где
Y–совокупность
первичных показателей состояния организма человека, по которыми в момент времени
T имеются результаты
обследования;
N –объем
Y.
Обозначим
m(O,G) =
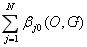 (9.20)
(9.20)
Из (9.8), (9.10), (9.11), (9.14), (9.19) и
(9.21) получаем
g (G) =
g (O,G), (9.21)
где
g (O,G)
= 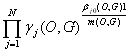 (9.22)
(9.22)
Как видно, для определения
g (G) вполне достаточно знание
данных по совокупности показателей Y(O,G)
и совершенно не требуется знания совокупности
Y(T,G).
Следовательно, тем более, не требуется знания системы S(T,G).
Обозначим через g min(G)
минимально возможное значение g
(G) для живого
организма:
g min(G)
> 0.. (9.23)
Можно показать, что
g (G) =
g min(G)
Û g j(G)
= g min(G)
для всех j = 1..N(G),
(9.24)
В самом деле, соглсно (7.12), имеет место
g j(G) =
g jmin(G) = g
min(G) при b j(G)
= 0, (9.25)
где
g min(G)
= 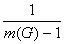 (9.26)
(9.26)
Так как
0 < g jmin(G)
< 1; j = 1..N(G),
в том случае, когда
g j(O,G)
= g j(G)
= g min(G)
для всех j = 1..N(G),
(9.27)
должно иметь место
b j0(O,G)
= 1 для всех j =1..N(G)
и, следовательно, согласно (9.21),
m(O,G) =
N(G)
С учетом этого из (9.22)
и (9.25) имеем
g (G) =
g min(G)
Û g j(G)
= g min(G)
для всех j = 1..N(G),
т.е. получаем (9.24).
Пусть
g (Z,G),
m(Z,G),
g j(Z,G)
и b
j0(Z,G)
- значения величин
g (G), m(G),
g j(G)
и b
j0(G)
такие, что имеют место
g (G) =
g (Z,G); m(O,G)
= m(Z,G);
g j(O,G)
= g j(Z,G)
и b j0(O,G)
= b j0(Z,G)
при P(G)
= P(Z,G),
(9.28)
где
P(Z,G) –
максимально- возможное для данного организма
значение P(G)
в момент времени T:
P(G) ≤ P(Z,G)
< 1. (9.29)
Согласно (9.22)
и (9.28) имеет
место
g (Z,G)
= 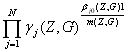 (9.30)
(9.30)
Величина g (Z,G),
установленная с доверительной вероятностью
P(Z,G)
с помощью зависимости (9.30),
служит оценкой состояния здоровья человека с
наивысшей точностью. Определить степень здоровья человека более точно -
невозможно.
Совокупность
B(G) = {Bjk(G);
k = 0,1; j = 1..N(G)},
как правило, является неизвестной. Поэтому на практике, обычно, оперируют
совокупностью
B = {Bjk;
k = 0,1; j = 1..N(G)}.
Пусть
g (Z), m(Z),
g j(Z)
и b
j0(Z)
- значения величин
g (Z,G),
m(Z,G),
g j(Z,G)
и b
j0(Z,G)
такие, что имеют место
g (Z) =
g (Z,G); m(Z)
= m(Z,G);
g j(Z)
= g j(Z,G)
и b j0(Z)
= b j0(Z,G)
при B = B(G),
(9.31)
Согласно (9.30) и (9.31)
имеет место
g (Z) =
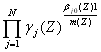 (9.32)
(9.32)
Полные
алгоритмы определения величин
g (O)
и g (Z)
опубликованы в
[12], [13] и [28].
10.Переносимость организмом человека врачебных и других воздействий.
Степень переносимости того или иного
воздействия организмом (СПЕВО) человека зависит как от состояния здоровья этого
человека, так и от величины и характера воздействия на его организм.
Пусть
m, g ,
g I и
b I0
- значения величин
m(O,G), g (O,G),
g I(O,G) и
b I0(O,G),
такие, что
m = m(O,G); g = g (O,G);
g I = g I(O,G);
b I0 = b
I(O,G) при B = B(G) (10.1)
Согласно (9.22) и (10.1) имеет место
g = 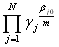 , (10.2)
, (10.2)
где
m = 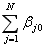 ³
N(O,G)
³ 1 (10.3)
³
N(O,G)
³ 1 (10.3)
Обозначим
G = g (Tk
– 1 ), если k
> 1 и 0
? g (Tk
– 1 ) ? g (Tk
)
и k = k0;
k0 = 1, 2,.. (10.4)
G = g (Tk
) , если k = 1
или k
> 1 и 0
< g (Tk
) < g (
Tk – 1 ) ,
где
g (Tk – 1
) = g (T0) =
1 и g (Tk
) = g (T1) =
g при
k = 1. (10.5)
Пусть, интервал времени
D Tk =
Tk – Tk
-1
таков, что для любого k = k0
(k0 = 1, 2,…)
имеет место
g (Tk – 1)
? g (t)
? g (Tk
) при Tk – 1
? t ?
Tk
или (10.6)
g (Tk – 1)
≥ g (t) ≥
g (Tk ) при
Tk – 1 ?
t ? Tk
Рассмотрим случай, когда
g (Tk - 1) = g
(Tk) = 1, (10.7)
Из (10.4) и (10.6) имеем
G = g (Tk - 1) =
g (t) = g
(Tk) = 1 при Tk
– 1 ? t
? Tk
Эта зависимость указывает на
то, что
обследуемый человек в течение всего времени от Tk
– 1 до Tk
находится в нормальном состоянии. Следовательно, в том случае, когда выполняется
условие (10.7), с вероятностью
P ≥ 0.95 можно утверждать,
что нагрузка H,
получаемая организмом обследуемого человека в течение времени от
Tk – 1
до Tk,
является в п о л н е п о с и л ь н о й.
Пусть, теперь, условие (10.7) не выполняется,
а имеет место
g (Tk – 1 ) ?
g (Tk) < 1
(10.8)
Из (10.4) и (10.8) получаем
G = g (Tk -1)
? g (t)
? g (Tk)
< 1 при Tk – 1
? t ?
Tk
В этом случае с вероятностью
P ≥ 0.95 можно утверждать,
что нагрузка H,
получаемая организмом обследуемого человека в течение времени от
Tk – 1
до Tk ,
является в п о л н е д о п у с т и м о й, н о н е в п о л н е п о с и л ь н о й.
На то, что нагрузка H
является вполне допустимой, указывает тот факт, что
выполняется условие: g (Tk – 1)
? g (Tk ),
т.е. величина g (Tk
) является не меньшей g
(Tk -1). А на то, что эта нагрузка еще не является вполне
посильной, указывает неравенство:
g (Tk) < 1.
Пусть, наконец, выполняется условие
g (Tk) <
g (Tk – 1 ) ? 1
и, следовательно, согласно (10.4), имеет место
G = g (Tk )
? g (t)
? g (Tk-1)
< 1 при Tk – 1
? t ?
Tk
Эта зависимость указывает на то, что в
результате врачебных или других воздействий в период времени от Tk -
1 до Tk
в организме человека произошли некоторые
отрицательные изменения, т.е. он подвергся нагрузке H,
которая не только не является посильной для
него, а является совершенно недопустимой.
Как видно, зная совокупность величин
g (Tk -1) и
g (Tk)
и, в конечном счете, согласно (10.4),
величину G, вполне однозначно можно судить о степени переносимости
организмом человека нагрузки Н в период времени от Tk –1
до Tk ;
эта степень является наивысшей, если
g (Tk –1) = g
(Tk) = 1
и, следовательно, согласно (10.4), имеет место: G = 1.
А если
g (Tk – 1) ?
g (Tk ) < 1
либо g (Tk)
< g (Tk - 1)
? 1,
то степень переносимости организмом человека нагрузки Н в период времени от Tk
–1 до Tk
является тем меньшей, чем
1) меньшей является величина
g (Tk),
2) большей является величина
g (Tk - 1),
т.е., в конечном счете, чем большей является величина: g
(Tk -1) - g (Tk) .
Ввиду того, что вообще
0 ? g (Tk –1)
и g (Tk)
? 1
и, следовательно,
? g (Tk - 1)
- g (Tk)?
? 1,
степень переносимости организмом человека нагрузки Н в период времени от Tk
–1 до Tk является н а и м е
н ь ш е й при g (Tk – 1) -
g (Tk ) = 1,
т.е. когда имеет место
g (Tk – 1) = 1
и g (Tk)
= 0 .
Но тогда, согласно (10.4) имеет место: G = 0,
т.е. в этом случае наименьшей является и величина
G.
Сказанное выше справедливо и в том
случае, когда k = 1, с одной оговоркой: при k = 1 в
качестве предыдущего фактического состояния организма человека выступает его
нормальное состояние и, следовательно, имеет место:
g (Tk – 1) = g
(T0) = 1. (10.9)
Так как вообще
g = g (Tk)
? 1; k = 1, 2, 3, … ,
при k = 1, согласно (10.9), имеем
g = g (T1)
? g (T0) = 1
и, в конечном счете, согласно (10.4): G = g ,
т.е. в том случае, когда k = 1, величина G
сводится к величине g .
Определение 13
Пусть, для любого k
= k0 (k0 =
1, 2,…) интервал времени D
Tk таков,
что выполняется условие (10.6).
Пусть, при
этом справедлива зависимость (10.4).
Тогда и только тогда с доверительной веротностью
P утверждают, что,
что величина G
представляет собой СПЕВО обследуемого человека.
Как видно, СПЕВО человека
G служит интегральной
характеристикой п р о ц е с с а, который при
каждом k = k0 ,
происходит в организме
человека в течение времени от
Tk – 1
до g (Tk).
Этим величина G
принципиально отличается от величины g . Эта
последняя, как указывалось выше, служит интегральной характеристикой
фактического состояния здоровья человека в вполне
определенном м о м е н т е времени
t = T.
Резюмируя, следует отметить, что зная
G, тем самим в распоряжении
специалиста имеется прямой ответ на вопрос: как организм человека перенес
нагрузку, полученную им в соответствующем периоде времени?
Таким образом, имеются все основания
говорить, что с точки зрения принятия врачебного решения, величина
G является более общей и,
следовательно, более важной характеристикой организма человека, чем величина
g .
Пусть
g (Z), m(Z)
и b
j0(Z)
–значения
g , m
и b
j0
такие, что имеют место
g = g (Z);
m = m(Z)
и b
j0 = b
j0(Z) Û
g j =
g j(Z)
для всех j = 1..N
Отсюда и из (10.2) и (10.3) имеем
g (Z) =
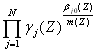 , (10.10)
, (10.10)
где
m(Z) =
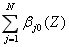 ³
N(O,G)
³ 1 (10.11)
³
N(O,G)
³ 1 (10.11)
Обозначим
G(Z) = g
(Z,Tk – 1 ),
если k
> 1 и 0
? g (Z,
Tk – 1) ?
g (Z,Tk
)
и k = k0;
k0 = 1, 2,.. (10.12)
G(Z) = g
(Z,Tk ),
если k = 1 или
k > 1
и 0 <
g (Z,Tk
) < g (Z,Tk
– 1),
где
g (Z,Tk
– 1) = g (Z,T0
) = 1 и g (Z,Tk
) = g (Z,T1)
= g при
k = 1.
Вообще
ç G - G(Z)ç
= 0, если человек здоров
и
ç G - G(Z)ç
³ 0, если человек болен.
Следует отметить, что если человек болен, то
врачу, в первую очередь, нужно знать, как реализуется та тактическая цель,
которую он при воздействии на организм больного ставил перед собой. С этой точки
зрения для врача величина G
является более важной характеристикой организма
больного, чем величина G(Z).
11. Распределение вероятностей Стьюдента и
воспринимаемые значения
первичных показателей состояния здоровья
человека
Можно показать, что
Nj1(G) =
m(G)
для всех j = 1..N(G)
(11.1)
и
Nj0(G) =
m(Z,G)
для всех j = 1..N(G)
(11.2)
Покажем сначала, что
Nj1(G) =
m*(G)
для всех j = 1..N(G)
(11.3)
и
Nj0(G) =
m*(Z,G)
для всех j = 1..N(G)
(11.4),
где
m*(G)
и m*(Z,G)
–некоторые фиксированные значения
m(G)
и m(Z,G)
соотвественно.
В самом деле, пусть, случайная величина Tj,
описываемая расспределением Стьюдента, такая что
Tj =
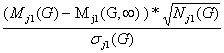 ; j
= j0; j0 =
1..N(G),
; j
= j0; j0 =
1..N(G),
где
Mj1(G,¥
) – генеральное среднее арифметическое в с е в о з
м о ж н ы х значений величины yj
Î Y для организма
данного человека в момент времени T:
Mj1(G) =
Mj1(G,¥
) при Bj1(G)
= Bj1(G,¥
);
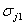 (G)
-«исправленное» среднеквадратичное
отклонение [29, с. 212]:
(G)
-«исправленное» среднеквадратичное
отклонение [29, с. 212]:
: 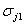 (G)=
(G)=
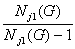 Sj12(G)
;
Sj12(G)
;
Для плотности распределения вероятностей S(t,nj)
случайной величины Tj
имеет место
S(t,nj) = B(nj) * [1 ,
(11.5)
,
(11.5)
где
nj = Nj1(G) и B(nj) =
 (11.6)
(11.6)
Здесь через g(x) обозначена гамма функция от x.
Как видно, плотность распределения Стьюдента S(t,nj)
однозначно определяется
объемом выборки nj и, следовательно, она не зависит от неизвестных
генеральных
параметров Mj1(G,¥ )
и Sj1(G,¥
),
где
Sj1(G,¥ ) –
генеральное среднеквадратическое отклонение в с е в
о з м о ж н ы х значений величины yj
Î Y для организма
данного человека в момент времени T:
Sj1(G) =
Sj1(G,¥
) при Bj1(G)
= Bj1(G,¥
)
Пусть
t(j) = t(P(G),
(nj -1)) (11.7)
- значение Tj такое, что
P(G) º
P(½ Tj½
< t(j)) = 2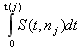 (11.8)
(11.8)
О величине t(j) говорят, что она является критическим значением
Tj при заданной
доверительной вероятности P(G)
и степени свободы (nj – 1)
Величина P(G)
для организма человека в каждый момент времени, как мы знаем. является вполне
определенной. Следовательно, эта величина никак не зависит от индекса j. Но
тогда, согласно (11.5), (11.7) и (11.8), от
индекса j не должны быть зависимыми и величины
nj; j = 1..
N(G)
т.е. должно иметь место
nj = m*(G)
для всех j = 1.. N(G)
Отсюда и из (11.6) имеем
Nj1(G) =
m*(G)
для всех j = 1..
N(G),
т.е. получаем (11.3).
Величины
Nj0(G);
j = 1…N(G),
являются конкретными значениями величин
Nj1(G);
j = 1…N(G)
Следовательно, для этих величин также должно иметь место
Nj0(G) =
m*(Z,G);
j = 1…N(G),
Покажем, теперь, что
m(G) = m*(G)
и m(Z,G) =
m*(Z,G)
(11.9)
Для величин
Njk(G);
k = 0.1; j = 1..N(G),
согласно (2.12), имеет место
3 ≤ Nj1(G) ≤ Nj0(G)
< ¥ ; j = 1..N(G)
C учетом этого из (11.3) получаем
3 ≤ m*(G) ≤
m*(Z,G)
< ¥ (11.10)
А для величин P(G)
и P(Z,G),
согласно (3.9), (4.1)
и (4.2) имеет место
0.5 ≤ P(G) ≤ P(Z,G)
< 1 (11.11)
Совокупность условий (11.10) и (11.11)
будет выполняться, если положим, что вообще
P(G) = 1 -
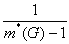 и P(Z,G)
= 1 -
и P(Z,G)
= 1 - 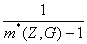 (11.12)
(11.12)
Величины P(G)
и P(Z,G),
как мы знаем,
определяются распределением Стьюдента по известным m*(G)
и m*(Z,G)
соответственно. Следовательно, эти величины, в
отличие от P, могут
принимать только определенные д и с к р е т
н ы е значения. Ими являются значения,
установленные с помощью зависимостей (11.12).
Согласно (11.12) имеет место
m*(G) = 1 +
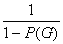 и m*(Z,G)
= 1 +
и m*(Z,G)
= 1 +  (11.13)
(11.13)
Вообще для величин P(G)
и P(Z,G),
согласно (3.1), (3.3), (3.4), (3.7), (3.9), (4.1) и
(4.2) имеют место
P(G) + P(B1) =1 и P(Z,G) +
Pmin(B1) =1,
P(B1) = 0.5 Û P(G) = 0.5 (11.14)
0 < Pmin(B1) ≤ P(B1) ≤ 0.5 и
0.5 ≤ P(G) ≤ P(Z,G) < 1
Сопоставляя совокупность зависимостей (11.14) с совокупностью (6.22),
(6.25) и (6.26), заключаем
P(B1) =
a (G); Pmin(B1)
= a (Z,G);
P(G) = C(G)
и P(Z,G)
= C(Z,G)
(11.15)
Согласно (7.3) и (11.15) имеет место [21]:
m(G) = 1 +
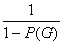 и m(Z,G)
= 1 +
и m(Z,G)
= 1 + 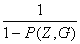 (11.16)
(11.16)
Отсюда и из (11.13) имеем
m(G) = m*(G)
и m(Z,G) =
m*(Z,G),
т.е. получаем (11.9).
Согласно (11.16) имеет место
m(G) ® m(Z,G)
® ¥ при P(G)
® P(Z,G) ® 1 (11.17)
а согласно (6.5), (6.22), (6.26) и (11.15) имеем
P(G) = 1 - max{a
j(G); j
= 1..N(G)}
и (11.18)
P(Z,G) =
1 - min{a
j(Z,G);
j = 1..N(G)}
12. Закономерности здорового организма
Пусть, человек находтся в нормальном состоянии
и, следовательно, имеют место
P(G) = P(Z,G);
Μj1(G) = Μj0(G);
Sj1(G) =
Sj0(G) и
Nj1(G) =
Nj0(G)
для всех j = 1..N(G)
(12.1)
Больной человек, как указывалось выше, не может
находиться в нормальном состоянии. Следовательно, если человек находится в
нормальном состоянии, то он является здоровым.
Согласно (5.33), (5.34), (11.4)
и (12.1) имеет место
d j(G)
= d jmin(G)
=d j(Z,G)
и (12.2)
t i(G) = t
jmin(G) = t (Z,G),
где
d j(Z,G) = Sj0(G)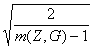 и t(Z,G) = t(P(Z,G), 2 (m(Z,G) – 1)) (12.3)
и t(Z,G) = t(P(Z,G), 2 (m(Z,G) – 1)) (12.3)
С учетом (12.2) из (5.23), (5.24) и (5.25) получаем
Sjmax(G) = Μj0(G)
- d j(Z,G)
t(Z,G)
(12.4)
А согласно (6.1), (6.2) и (12.3) имеет место
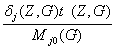 =
a (Z,G)
для всех j = 1..N (12.5)
=
a (Z,G)
для всех j = 1..N (12.5)
Обозначим
hmin(Z,G)
= 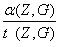 (12.6)
(12.6)
Согласно (12.5 и (12.6 )
имеет место
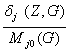 = hmin(Z,G)
для всех j = 1..N, (12.7)
= hmin(Z,G)
для всех j = 1..N, (12.7)
Отсюда и из (12.3) получаем
hmin(Z,G)
= 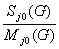
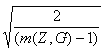 ; j
= 1..N (12.8)
; j
= 1..N (12.8)
Обозначим
h(Z,G) =
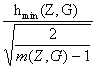 (12.9)
(12.9)
Согласно (12.18) и (12.19) имеет место
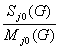 = h(Z,G)
для всех j = 1..N, (12.10)
= h(Z,G)
для всех j = 1..N, (12.10)
В том случае, когда выполняется условие
ç Μj1 - Μj0
ç < d
*j t *j
для всех j = 1..N(G) (12.11)
с доверительной вероятностью P можно утверждать, что человек находится в
нормальном состоянии в обычном смысле. К тому же
это утверждение является субьективным, ибо
величина P задана специалистом и, следовательно, является субьективной
характеристикой состояния здоровья человека. Другое дело, когда выполняется
условие
ç Μj1(G) -
Μj0(G)
ç < d
j(Z,G) t(Z,G)
для всех j = 1..N(G) (12.12)
В этом случае утверждение о том, что человек находится в нормальном состоянии
справеливо с
доверитеьлной вероятностью P(Z,G).
И это утверждение является объективным, ибо величина P(Z,G)
для организма человека является вполне
определенной, т.е. объективной характеристикой. А вообще утверждеие о том, что
человек находится в нормальном состоянии, является объективным,
если
ç Μj1(G) -
Μj0(G)ç
< d j(G)
t j(G)
для всех j = 1..N(G) (12.13)
Но это утверждение справедливо с доверительной веротностью P(G)
и, следовательно, оно является менее
надежным, чем утверждение, основанное на
выполнении условия (12.12). Это обусловлено тем, что вообще P(G)
£ P(Z,G).
Зависимости (12.7)
и (12.10)
справедливы в том случае, когда выполняется условие (12.12).
Следовательно, эти зависимости отображают н а и б о л е е
н а д е ж н ы е
объективные свойства зорового организма.
Определение 14
Пусть процессы, происходящие в организме
человека в момент времени Т такие, что имеют место
Mj1(G) = Mj0(G)
Sj1(G) = Sj0(G)
для всех j = 1..N(G) (12.14)
d j(
G) = d j(Z,G)
Тогда и только тогда с вероятностью P(G)
утверждают, что
в момент времени Т состояние здоровья человека является н о р м а л ь н ы
м в а б с о л т н о м с м ы с л е .
Согласно (12.7)
и (12.10) имеет
место
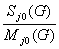 = h(O,Z)
> 0 Û
= h(O,Z)
> 0 Û
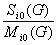 = h(O,Z)
> 0 для всех i,j
= 1..N(G)
= h(O,Z)
> 0 для всех i,j
= 1..N(G)
и (12.15)
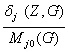 = hmin(O,Z)
> 0 Û
= hmin(O,Z)
> 0 Û
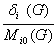 = hmin(O,Z)
> 0 для всех i,j
= 1..N(G)
= hmin(O,Z)
> 0 для всех i,j
= 1..N(G)
Совокупность зависимостей (12.15), как видно,
является справедливой только в том случае, когда человек находится в
нормальном состоянии в обсолютном смысле и, следовательно, он является здоровым.
Обратное утверждение, однако, не верно: если человек здоров, то его организм
может находиться в нормальном состоянии, а может и
- нет.
Организм здорового человека находится в
нормальном состоянии в широком смысле, если выполняется условие (12.12). А если
выполняется условие (12.11), то организм здорового человека находится в
нормальном состоянии в узкоком смысле.
Определение 15
Пусть, в момент времени T
имеют место
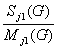 = h(O,Z)
> 0 Û
= h(O,Z)
> 0 Û
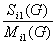 = h(O,Z)
> 0 для всех i,j
= 1..N(G)
= h(O,Z)
> 0 для всех i,j
= 1..N(G)
и (12.16)
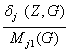 = hmin(O,Z)
> 0 Û
= hmin(O,Z)
> 0 Û
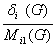 = hmin(O,Z)
> 0 для всех i,j
= 1..N(G)
= hmin(O,Z)
> 0 для всех i,j
= 1..N(G)
Тогда и только тогда с вероятностью
P(G)
утверждают, что в организме человека в момент времени T
происходят с о з и д а т е л ь н ы е п р о ц е с с
ы.
В организме здорового человека, согласно
(12.15), всегда присходят созидательные процессы. А в организме больного
созидательные процессы могут происходить или не происходить.
Обозначим
D j(G)
= (1 – P(G)) Mj0(G)
(12.17)
О величине D j(G)
говорят, что она является с и с т е м н о й е д и н
и ц е й измерения yj в организме
человека в момент времени T.
Согласно (11. 22) и (12.17) имеет место
D j(G)
³ d j(G)
t j(G) (12.18)
О произведении d j(G)
tj(G) говорят,
что оно является единицей измерения yj
в j –ой функциональной части организма человека в момент
времени T. Говорят также,
что это произведение является л о к а л ь н о й е д и н и ц е й измерения
yj в организме человека в момент времени
T.
Зависимость (12.17) указывает на то, что
величина yj
в соответствующей функциональной части всегда
измеряется точнее.
Так как
P(G) ≤ P(Z,G),
в общем случае имеет место
D j(G)
³ D j(Z,G),
(12.19)
где
D j(Z,G)
–значение D j(G)
для организма здорового человека:
D j(Z,G)
= (1 – P(Z,G))
Mj0(G) (12.20)
Если человек здоров, то P(G)
= P(Z,G)
и, следовательно, согласно (11.19), имеет место
a j(G)
= a j(Z,G)
= a min(Z,G)
для всех j = 1..N(G),
(12.21)
где
a min(Z,G)
= min{a j(Z,G);
j = 1..N(G)}
(12.22)
Из (6.1), (6.2) и (12.21) получаем
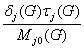 =
=
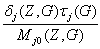 = a
min(Z,G)
= a
min(Z,G)
или
D j(G)
= d j(G)
t j(G) =
d j(Z,G)
t j(Z,G)
= D j(Z,G),
(12.23)
где
D j(Z,G)
= a min(Z,G)
Mj0(G)
(12.24)
Итак, в здоровом организме величины
yj; j = 1..N(G)
всегда измеряются с н а и б о л ь ш е й т о ч н о с т ь ю. А благодаря этому
имеют место
aj(O,Z)
= aj(O,L,Z)
для всех j = 1..N(G),
(12.25)
где
aj(O,Z)
– системное предельно допустимое значение величины
yj;
aj(O,L,Z)
– локалное предельно допустимое значение величины
yj.
Зависимость (12.24) указывают на то, что в
здоровом организме предельно допустимые значения первичных показателей являются
н а и б о л е е о т д а л е н н ы м и о т и х и н д и в и д у а л ь н ы х н о р
м. Именно этим обусловлено то, что возможности здорового организма всегда
являются н а и б о л ь ш и м и.
Еще раз следует отметить, что зависимости
(12.23) и (12.25) справедливы только для организма
человека, который является здоровым в обсолютном смысле. А в общем случае
имеют место
D j(G)
³ d j(G)
t j(G)
³ d j(Z,G)
t j(Z,G)
³ D j(Z,G);
j = 1..N(G),
и (12.26)
aj(O,G)
³ aj(Z,G);
j = 1..N(G)
и, следовательно, выполняется условие
½ Μj0(G)
- aj(O,G)
½ £ ½
Μj0(G) -
aj(Z,G)½
Ввиду этого для ж и в о г о организма
справедлива зависимость
0 £ ½ Μj1(G)
- aj(O,G)
½ £ ½
Μj0(G) -
aj(O,G)
½ £ ½
Μj0(G) -
aj(Z,G)½
Именно справедливостью этой зависимости объясняется тот факт, что здоровый
взрослый человек запросто поднимает 50 и более кг тяжести, а человек с ИБС
получает инфаркт при поднятии 10 кг.
Итак, главная особенность здорового организма:
первичные показатели его состояния имеют наиболее отдаленные от их
индивидуальных норм предельно допустимые значения.
В целом настоящая статья приложена к документу «Описание изобретения» заявки
[28] под названием: «Математическое обоснование
способа количественного измерения здоровья больного с пневмонией». Лвиная доля
материалов настоящей статьи опубликована в [30].
Заключение.
1. Величина g
(G), установленная с помощью
зависимости (9.8), удовлетворяет не только условие объективности, но и условие
единственности решения.
Выполнение условия единственности решения
обусловлено тем, что система S(T,G)
является уникальной, т.е. е д и н с т в е н н о й ц
е л о с т н о й системой, которая в момент времени T
несет ответственность за получение «желаемого конечного результата» каждым живим
организмом.
2. Результат, полученный с помощью зависимости
(9.22) является наиболее близким к истине в том случае, когда выполняется
условие
Y = Y(P,G).
А если это условие не выполняется, а имеет место
Y(P,G)
Í Y,
то вероятность того, что результат может оказаться
з а в ы ш е н н ы м, будет тем больше, чем
больше разность
Y - Y(P,G).
В связи с этим возрастает необходимость установления множества
Y(P,G) =
Y(T,G)
для всевозможных ненормальных состояний каждой поло
–возрастной группы людей. А это можно сделать, установив всевозможные системы
типа S(T,G).
3. Выше изложенный аппарат, в первую очередь,
предназначен для системного анализа состояния
здоровья человека. Однако этот аппарат вполне можно применять и
к другим живым системам.
Вообще, ввиду того, что живой организм
является выраженной целостной системой, настоящий аппарат применим
к любой
целостной системе. Благодаря своей высочайшей общности он
будет стимулировать дальнейшее усовершенствование
систем искусственного интеллекта.
Литература
1. Царенко С.В., Болякин Г.К. Доказательная
медицина и критические состояния. http://www.medolina.ru
2. Власов В.В. Введение в доказательную
медицину.–М.: Медиа Сфера, 2001.–392 с.
3. Каменская В.Н., Каменская М.А., Болякина
Г.К., Борисова Л.Ф. Методология доказательной медицины (evidence-based medicine)
в клинической практике специалистов по медицине критических состояний (обзор
литературы) // Вестн. интенс. терап.–2000.– № 2.– С. 3-11.
4. Хускивадзе А.П., Хускивадзе А.А. Способ определения степени здоровья
человека. Патент России RU №
2141791,- 1999
5 Дзидзигури
Л.М. Значение иммунной системы в патогенезе атеросклероза и ишемической болезни
сердца. Автореф. Диссерт. на соискание ученой степени докт.мед. наук: 14.00.06 и
14.00.36. – Ереван. – 1989.
6. Давитая Г.Ш. Острый живот у детей (
клинико-экспериментальное исследование).- Диссерт. на соискание ученой степени
докт.мед. наук. – М . – 1988. – 250 с.
7. Датешидзе М.Н. Состояние иммунного статуса
больных с ревматоидным артритом. - Диссерт. на соискание ученой степени канд.
мед. наук: – Тбилиси . – 1990. – 120 с.
8. Рачвелишвили Н.В. Клинико-прогностическое
значение субпопуляционных
иммуннокомпетентных клеток при хроническом гепатите и циррозе печени вирусной
и алкогольной природы. Диссерт. на соискание ученой степени канд. мед. наук: –
Тбилиси . – 1990. – 154 с.
9.Какауридзе Н.Г. Изменение некоторых
микроструктур кожи при атеросклерозе. Диссерт. на соискание ученой степени канд.
мед. наук: – Тбилиси . – 1993. – 172 с.
10 Антипова О.С. Моделирование, алгоритмизация и
рациональная диагностика тревожно- депресивных расстройств на этапе амбулаторной
психиатрической помощи. Автореф. Диссерт. на соискание
ученой степени КМН: 05.13.01.–Воронеж.–2004.–23
с.
11 Хускивадзе А.П., Долгополов Д.М., Долгополов М.А., Хускивадзе А.А. Система
слежения за состоянием здоровья человека. Заявка на изобретение № RU (21)
2002120986 /14 (13) A , кл. МПК 7 А 61 В 05/00.–2004. Бюл. № 6.
12. Хускивадзе А.А., Хускивадзе А.П. Определение степени переносимости
организмом больного тревожно-депресивными растройствами врачебных и других
воздействий.
RU 2007140016.A.-2008.-Бюл.№ 13
13. Хускивадзе А.А., Хускивадзе А.П. Определение степени переносимости
организмом больного с пневмонией активной ортостатической пробы. RU 2007 144
803. A. -.2008. -Бюл. № 16
14. Баевский Р.М. Прогнозирование состояний на грани нормы и патологии. - М.-
Медицина -1979. – 312 с.
15. Большев Л.М. , Смирнов М.В. Таблицы математической статистики.–М.–Наука
-1983.
16. Хускивадзе А.А., Хускивадзе А.П. Вероятностный предел познания истины и
вопросы математического моделирования живого организма как единого целого.
http://www.medlinks.ru/article.php?sid=32701
17. Хускивадзе А.А., Хускивадзе А.П. Естественный глобальный оптимум и
вероятностный предел познания истины. Индивидуальная норма человека.
http://www.medlinks.ru/article.php?sid=33435
18.Афанасьев В.Г. Системность и общество
- М.:-Изд. полит. Литературы.-1980.-368 с.
19.Афанасьев В.Г. Общество, системность,
познание и управление.- М.:-Изд. полит. литературы.-1981.-305
с.
20.Афанасьев В.Г. Проблема целостности в
философии и биологии - М.:-«Мысль».-1964
21.Тигранян Р.А. Стресс и его значение для
организма. – М.:- Наука.- 1988.- 176 с.
22. Селье Г. Стресс без дистресса.-М.:-
Прогресс.-1970.- 123 с.
23. Хускивадзе А.П. Задачи
многокритериальной оптимизации и оценивания в эмпирических
целостных системах и их
решения.–Тбилиси.–Изд. «Сакартвело».–1991.–118 с.
24 Кавилашвили Д.Ш. Применение статистических
методов в психологии (на грузинском языке).–Тбилиси.-Изд. ТГУ. -1974.-248 с.
25. Анохин П.К. Очерки по физиологии
функциональных систем –М.:Медицина.–1975.
26.Анохин П.К. Принципы системной организации
функций– М.–Наука.–1973.
27. Функциональные системы организма.–Под
редакцией К.В. Судакова.–М.:-Медицина. –
1987.–432 с.
28. Хускивадзе А.А., Хускивадзе А.П. Способ определения
степени переносимости организмом больного с
пневмонией активной ортостатической пробы. RU 2008
140 229 A. -.2008.
29. Гмурман В.Е. Теория вероятностей и
математическая статистика. –М. –Высщ. Школа, -2002.-479 с.
30. Хускивадзе А.А., Хускивадзе А.П. Количественное измерение здоровья
человека.
http://www.medlinks.ru/article.php?sid=34243

