Данная информация предназначена для специалистов в области здравоохранения и фармацевтики. Пациенты не должны использовать эту информацию в качестве медицинских советов или рекомендаций.
Естественный глобальный оптимум
и вероятностный предел познания истины
Индивидуальная норма человека
А.А. Хускивадзе1,
А.П. Хускивадзе
Аннотация
В статье изложено математическое
обоснование способа определения
индивидуальных норм показателей состоянии здоровья человека.
Введено понятие целостной системы и показано, что
индивидуальная норма человека представляет
собой естественный глобальный оптимум
организма этого человека как целостной системы. Приведено математическое
обоснование понятия вероятностного предела
познания истины, введенного в [1].
Доказано, что каждая целостная система,
включая живой организм, имеет свой вероятностный
предел познания истины, который определяется естественными глобальными
оптимумами первичных показателей состояния этой целостной системы.
Статья представляет интерес для специалистов,
работающих на стыке медицины, биологии, физики и философии.
Ключевые слова: индивидуальная норма,
глобальный оптимум, живой организм, нормальное состояние,
целостная система, познание истины.
Введение
В современной медико-биологической литературе
часто встречаются выражения: «Целостный организм», «Живой организм является
выраженной целостной системой» и т.д. Эти выражения многократно используются,
например, в работах [2] и [3].
Тем не менее, единой общепризнанной формулировки понятия «Целостная система»
еще не существует. Тем более, не существует общей математической теории
целостных систем.
Результаты наших первых исследований по созданию
общей математической теории целостных систем представлены в [4].
Последующие наши
результаты нашли отражение в [5]
и [6]. Ниже излагаются
некоторые новые результаты.
1. Суммативные и целостные системы
Понятие «Множество», как известно, является
первичным математическим понятием. Если множество бинарное, то говорят, что оно
является отношением.
Итак, пусть
0 < yj <
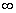 ; j
=1..N; N
<
; j
=1..N; N
< 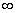
-являются скалярными измеряемыми величинами, каждая j-ая
из которых имеет трех или более возможных значений.
Обозначим
Y= í yj
; j=
1..N}(1)
Пусть
A, Aj;
j=1..N
- непустые конечные множества, а
Hи
Hj ; j
=1..N
- непустые конечные множества отношений такие, что для каждой пары
Sj= < Aj
, Hj> ;….. j
= j0 ;……j0
=1..N
имеет место
Sj= Sj0
Û yj=
yj0 ,
а для пары S= < A,
H> выполняется условие
S= S0
Û Y= Y0
,
т.е. вообще имеют место
S = S0 Û
Y = Y0
и Sj = Sj0 Û
yj=
yj0
; j
=1..N
, (2)
где S0, Y0,
Sj0 и
yj0
являются фиксированными значениями S,
Y, Sj
и yj
соответственно.
Определение 1
Пусть, имеет место (2) и при этом
2 ≤ N и S= S0
Û Sj=
Sj0 для всех j
=1.. N(3)
Тогда и только тогда говорят, что пара
Sявляется с и с т е м о й
элементов
Sj; j
=1..N.
О каждой паре Sj
говорят, что она является j
–о й ф у н к ц и о н а л ь н о й ч а с т ь ю
системы S.
Если N= 1,
т.е. имеет место S=
S1, то о паре
Sговорят, что она
является э л е м е н т о м системы.
Определение 2
Пусть, пара S
является системой, т.е. выполняется совокупность
условий (2) и (3).
Тогда и только тогда говорят, что множество (1)
является генеральной совокупностью первичных показателей состояния системы
Sи пишут:
Y= Y(S,G)
º í yj
; j
=1..N(S,G)},
(4)
где N(S,G)
– объем Y(S,G).
Согласно (1) и (4) имеем
N= N(S,G)
Следовательно, можно говорить, что система
Sсостоит из
N(S,G)
количества функциональных частей.
Вообще
2 ≤ N(S,G)
≤ M(A) <
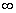 ,
,
где M(A) – объем
A.
В виду того, что
H¹ Æ
, (5)
элементы системы S, в
отличие от элементов множества A,
всегда являются взаимно связанными. Эта
взаимосвязанность выражается в том, что процессы, происходящие в элементах
системы S, являются в
той или иной, о т л и ч н о й о т н у л я, степени согласованными.
Тот факт, что процессы, происходящие в элементах
системы S, являются в
той или иной, о т л и ч н о й о т н у л я, степени согласованными, со своей
стороны, указывает на то, что в системе S
производится измерение величин
yj; j= 1..N(S,G).
(6)
В противном случае, не могло бы иметь места какое-то, отличное от нуля,
согласование между процессами, происходящими в элементах системы
S.
Следовательно, система S
должна иметь свою, вполне определенную, единицу измерения каждой величины
yj. Обозначим эту
единицу через D j(S,G).
Каждая j–ая
функциональная часть системы S,
со своей стороны, то же является системой.
Следовательно, и эта функциональная часть должна иметь свою, вполне
определенную, единицу измерения каждой величины yj
.
Вообще
D j(S,G) ³
D (j,S,G) > 0 ; j = 1..N(S,G), (7)
где
D (j,S,G)
– единица измерения величины
yj, применяемая
на местном уровне, т.е. в самой j–ой
функциональной части системы S.
Применяя величину D
(j,S,G)
в качестве единицы измерения, тем самым, признают
справедливым следующее положение.
Предположение
Все значения величины yj
от yj-
D (j,S,G)
до yj+
D (j,S,G)
являются друг от друга н е р а з л и ч и м ы м и.
Пусть
Bj1(S,G)
= {bjl 1(S,G);
l = 1..Nj1(S,G)} ;
j = j0 ; j0 = 1..N(S,G)
-генеральная совокупность значений величины
yj, р а з
л и ч а е м ы х д р у г о т д р у г а в системе S
в данный момент времени,
где
Nj1(S,G) –
объемы Bj1(S,G)
.
Пусть
Bj1; j =
j0 ; j0 = 1..N(S,G)
– непустое подмножество Bj1(S,G)
такое, что
1. Оно установлено в результате наблюдения за
системой Sизвне.
2. Множество Bj1
представляет собой результаты равноточных и взаимно
независимых измерений величины yj.
3. Систематические ошибки измерений величины
yj
отсутствуют.
4. Случайные ошибки измерений величины
yjописываются
стандартным нормальным распределением вероятностей, т.е. имеет место:
D (yj,S,G)
= 0,
где
D (yj,S,G)
– генеральное среднее арифметическое случайных
ошибок измерений величины yj
в системе S.
5 Множество Bj1
с доверительной вероятностью
Pj³ 0.5
служит репрезентативной выборкой из совокупности
Bj1(S,¥
),
где
Bj1(S,¥
) – генеральная совокупность в с е в о з м о ж н ы х значений величины
yj, в системе
Sв данный момент
времени:
Bj1(S,G)
Í Bj1(S,¥
).
Обозначим через Pj(S,G)
значение Pj
такое, что
Pj = Pj(S,G) Û
Bj1
= Bj1(S,G).
Вообще
Pj(S,G) ® 1 при
Bj1(S,G)
® Bj1(S,¥
)
и
Bj1(S,G).®
Bj1(S,¥
) при D (j,S,G)®
0
Отсюда
Pj(S,G) ® 1 при
D (j,S,G) ® 0 (8)
Принимая во внимание зависимость (8), о величине Pj(S,G)
можно говорить, что она является вероятностью того,
что все значения величины yj
от yj-
D (j,S,G)
до yj+
D (j,S,G)
являются друг от друга неразличимыми.
Величина Pj(S,G),
по определению, является некоторым значением
вероятности Pj³
0.5. Следовательно, должно иметь место:
. Pj(S,G)
³ 0.5.
С учетом этого из (7) и (8) получаем
0.5 ≤ Pj(S,G)
< 1; j = 1..N(S,G)
и, в конечном счете,
0.5 ≤ P(O,S,G) ≤ P(Z,S,G) < 1
где
P(O,S,G) = min{Pj(S,G); j
=1..N(S,G)}
и (9)
P(Z,S,G) = max{Pj(S,G); j
=1..N(S,G)}
Пусть,
γ(S,G)
Î [0,1]
– скалярная величина, такая, что
1. Выполняется условие
γ(S,G) = 0 при
H= Æ
и (10)
0 < γ(S,G)
при H
¹ Æ
2. Справедлива зависимость
γ(S,G) = 1 Û P(O,S,G) = P(O,S,G)
(11)
Согласно (10) имеет место
0 < γ(S,G)
Û H¹
Æ
Следовательно, величина γ(S,G)
является такой же важной характеристикой системы
S, какою для этой
системы является величина H.
Вместе с тем, для величины γ(S,G)
справедлива и зависимость (11), что делает эту
величину более определенной.
Определение 3
Пусть, имеют место (10) и (11).
Тогда и только тогда говорят, что величина γ(S,G)
служит общей характеристикой
с о г л а с о в а н н о с т и процессов,
происходящих в элементах системы S.
Обозначим
r (S,G)
= 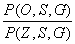 (12)
(12)
Пусть, имеет место
r (S,G)
= 1
и, следовательно, согласно (12), выполняется условие
P(O,S,G)
= P(Z,S,G)
В этом случае, согласно (11), будет иметь место
зависимость γ(S,G) = 1,
указывающая, что процессы, происходящие в элементах
системы S, являются
наиболее согласованными.
Определение 4
Говорят, что система S
находится в н о р м а л ь н о м с о с т о я н и и,
если имеет место: γ(S,G) =
1.
А если
0 < γ(S,G)
< 1,
то говорят, что система S
находится в одном из возможных н е н о р м а л ь н ых
с о с т о я н и й.
В том случае, когда
γ(S,G)
= 0,
говорят, что система S
находится в н е о п р е д е л е н н о м с о с т о я н и и.
В последующих публикациях мы покажем, что
понятие нормального состояния, применяемое в современной медицине и понятие
нормального состояния, применяемое в физике, являются частными выражениями
введенного выше.
Итак, если γ(S,G) = 1,
то ф а к т и ч е с к и м состоянием системы
Sявляется ее нормальное
состояние в с а м о м ш и р о к о м с м ы с л е этого слова. А если
γ(S,G) < 1,
то фактическое состояние системы
Sотличается от ее
нормального состояния.
Определение 5.
Пусть, множество возможных состояний системы
Sупорядочено таким образом, что чем больше γ(S,G),
тем фактическое состояние этой системы ближе
к ее нормальному состоянию.
Тогда и только тогда о величине γ(S,G)
говорят, что она является а н а л и т и ч е с к о й
м е р о й б л и з о с т и с о с т о я н и я системы S
к ее возможному нормальному состоянию.
О величине r (S,G)
говорят, что она является в е р о я т н о с т н о й
м е р о й б л и з о с т и с о с т о я н и я системы S
к ее возможному нормальному состоянию.
Обозначим через
Bj0(S,G)
, bjl 0(S,G)
и Nj0(S,G)
- значения величин
Bj1(S,G)
, bjl
1(S,G) и
Nj1(S,G)
таких, что
Bj1(S,G)
= Bj0(S,G)
,bjl
1(S,G) =bjl
0(S,G) и
Nj1(S,G)
= Nj0(S,G)
при P(O,S,G) = P0(O,S,G) = P(Z,S,G),
т.е. вообще
Bj0(S,G)
= {bjl
0(S,G); l
= 1..Nj0(S,G)}
Так как вообще P(O,S,G)
≤ P(Z,S,G),
должно иметь место
Bj1(S,G)
Í Bj0(S,G);
j=
1..N(S,G)
Как видно, совокупность
Bj0(S,G);
j=1..N(S,G)
служит характеристикой н о р м а л ь н о г о состояния системы
S, а совокупность
Bj1(S,G);
j=1..N(S,G)
является характеристикой ее ф а к т и ч е с к о г о состояния.
Пусть
γj(S,G); j
=1..N(S,G)
- скалярные величины, такие что
1. Имеет место
γj(S,G)
= 0 при Hj
= Æ
и
γj(S,G)
Î (0,1] при
Hj¹
Æ ,
т.е. вообще
γj(S,G) Î [0,1] );
j=
1..N(S,G).
2. Если
H¹ Æ
и Hj
¹ Æ
для всех j
=1..N(S,G),
то
γj(S,G) = γj(Mjk(S,G),
Sjk(S,G), Njk(S,G); k = 0,1; j
=1..N(S,G));
j=
1..N(S,G)
(13)
и
γ(S,G) =1 Û γj(S,G)
= 1 для всех
j=
1..N(S,G),
(14)
где
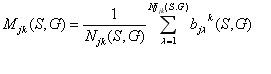
и
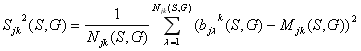
Определение 6.
Пусть, вместо (13) выполняется условие
γj(S,G)
= γj(Mjk(S,G),
Sjk(S,G),
Njk(S,G);
k= 0,1); j=
1..N(S,G)).
Пусть, к тому же имеет место
γ(S,G)
= 0 Û
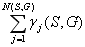 = 0
= 0
Тогда и только тогда говорят, что система
Sявляется с у м м а т и в н
о й и пишут:
γ(S,G)
= 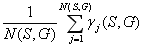 (15)
(15)
Определение 7.
Пусть, имеют место (13) и (14) и при этом
выполняется условие
γ(S,G)
¹ 0 Û
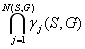 ¹
0
¹
0
Пусть, при этом
P(O,S,G) = P(Z,S,G) = P(S,G),
где
P(S,G) –
значение P(O,S,G)
такое, что имеют место
P(O,S,G) = P(S,G) Û P(O,S,G) =
P(Z,S,G) (16)
и
0.5 ≤ P(S,G)
< 1 (17)
Тогда и только тогда с вероятностью
P(O,S,G)
= P(S,G)
утверждают, что система S
является ц е л о с т н о й и пишут:
γ(S,G)
= 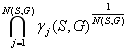 , (18)
, (18)
Определение 8
Пусть
P(O,S,G)
= P(S,G) ≥
0.95 (19)
Тогда и только тогда говорят, что
Sявляется в ы р а ж
е н н о й ц е л о с т н о й с и с т е м о й.
А если
P(O,S,G) = P(S,G) = 0.5, (20)
то говорят, что S
является с и с т е м о й н е о п р е д е л е н н о й ц е л о с т н о с т и: она
является и не является целостной системой одновременно.
2. Живой организм, как выраженная целостная
система.
Объективная и субъективная вероятностные пределы
познания истины.
Согласно (16) и (19) имеет место
P(O,S,G) = P(Z,S,G) = P(S,G) ≥ 0.95 (21)
Отсюда и из (11) имеем
P(O,S,G) = P(S,G) ≥ 0.95 Þ γ(S,G)
= 1 (22)
Таким образом, выраженная целостная система всегда находится в н о р м
а л ь н о м состоянии.
Надо полагать, что любой живой организм будет
являться выраженной целостной системой, если γ(S,G)
= 1. А если γ(S,G)
< 1, то живой организм будет тем менее выраженной
целостной системой, чем γ(S,G)
будет ближе к нулю.
Можно показать, что для систем с неопределенной
целостностью одновременно имеют место:
γ(S,G)
= 1 и γ(S,G)
¹ 1.
В самом деле, пусть, имеет место (20). Тогда,
согласно (16), во -первых, будет иметь место
P(Z,S,G)
= 0.5
Во –вторых, будет выполняться равенство
P(O,S,G)
= P(Z,S,G).
Отсюда и из (11) и (12) имеем
γ(S,G) = 1
Как видно, условие γ(S,G)
= 1 выполняется с вероятностью, равной 0.5.
Следовательно, с вероятностью 0.5 должно выполняться условие: γ(S,G)
¹ 1.
Примером системы с неопределенной целостностью
может служить любая идеальная пара противоположных материальных реальностей.
Например,. в качестве такой системы может быть рассмотрена пара: «Электрон +
позитрон». В качестве другого примера может служить пара, составленная типичными
представителями (ТП) особ противоположных полов одного и того же биологического
вида.
Таким образом, о системе с неопределенной
целостностью можно говорить также, что она является и д е а л ь н о й п а р о й
п р о т и в о п о л о ж н ы х м а т е р и а л ь н ы х реальностей.
Согласно (9) имеет место
P(O,S,G)
≤ P(Z,S,G)
(23)
С учетом этого из (16) получаем
P(O,S,G)
≤ P(S,G),
(24)
т.е. величина P(S,G)
является н а и б о л ь ш и м возможным значением
P(O,S,G).
Следовательно, познание внутреннего мира системы
Sболее точно
является принципиально невозможным.
Определение 9.
Пусть, для любой системы
Sимеют место зависимости (11) и (16) и при
этом выполняется условие
P(S,G) = P(S0,G) при S = S0
,
где P(S0,G)
– фиксированное значение P(S,G).
Тогда и только тогда говорят, что P(S,G)
является в е р о я т н о с т н о й
м е р о й ц е л о с т н о с т и системы
S.
Говорят также, что P(S,G)
является о б ъ е к т и в н ы м в е р о я т н
о с т н ы м
п р е д е л о м п о з н а н и я и с т и н
ы в с и с т е м е S.
3. Индивидуальная точечная норма
Пусть, C(S,G)–генеральная
совокупность возможных ненормальных состояний системы S.
Пусть, далее Y(r,S,G)
– совокупность первичных показателей r–го
возможного состояния системы S
такая, что
yj Î Y(r,S,G) Û
Вер{ú Mj1(r,S,G) -
Mj0(S,G)ú > 0} > 0, (25)
где
Mj1(r,S,G)
– фиксированное значение Mj1(S,G):
Mj1(r,S,G) = Mj1(S,G) при r = r0;
r0 = 1, 2, 3,…
Множество Y(r,S,G),
как видно из (25),
составлено теми первичными показателями, каждый
j–ый из которых при r–ом
ненормальном состоянии системы S
в о о б щ е
может быть отклонен от Mj0(S,G).
Следовательно, из совокупности показателей
Y(r,S,G)
в одних случаях от своих статистических норм
фактически могут быть отклоненными в с е без исключения, в других случаях –
только какая-та ч а с т ь
из них. Причем, для одной системы эта часть
будет одной, для другой системы- другой и т.д.
Определение 10
Пусть
Y(r,S,G) = Y0(r,S,G) Û S = S0
и r = r0 ; r0 = 1..R(S,G)
и, следовательно,
N(r,S,G) = N0(r,S,G) при S = S0
и r = r0 ; r0 = 1..R(S,G),
где
Y0(r,S,G)
– фиксированное значение Y(r,S,G);
R(S,G) - объем C(S,G);
N(r,S,G)
и N0(r,S,G)
– объемы Y(r,S,G)
и Y0(r,S,G)
соответственно.
Тогда и только тогда говорят, что Y(r,S,G)
является г е н е р а л ь н о й совокупностью
первичных показателей r–го
ненормального состояния системы S.
Вообще
Y(r,S,G) Ì Y(Z,S,G) º
Y(S,G),
где
Y(Z,S,G)
– генеральная совокупность первичных показателей
нормального состояния системы S.
Пусть, L–
конечное множество систем такое, что если
SÎ L,
то имеют место:
C(S,G) = C(G); Y(Z,S,G) = Y(Z,G) и
Y(r,S,G) = Y(r,G)
для всех r= 1.. R(S,G)
(26)
и, следовательно
R(S,G) = R(G); N(Z,S,G) = N(Z,G) и N(r,S,G) = N(r,G)
для всех r = 1.. R(S,G),
где
C(G), Y(Z,G), Y(r,G), R(G), N(Z,G) и N(r,G)
-фиксированные значения
C(S,G), Y(Z,S,G), Y(r,S,G), R(S,G), N(Z,S,G) и N(r,S,G)
соответственно.
Обозначим
Dj0 (G) = {Mj0(S,G); S = 1..N(L)}
и
Dj1(r,G) = {Mj1(r,S,G); S = 1..N(L)},
где N(L) – объем
L:
N(L) <
¥
Пусть, множество L
такое, что
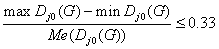 для всех
j= 1..N(G)
для всех
j= 1..N(G)
и (27)
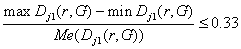 для
для
всех j= 1..N(G)
и r= 1.. R(G)
где
Me(Dj1(G))
– медиана совокупности Dj0 (G);
Me(Dj1(r,G))
– медиана совокупности Dj1(r,G).
Определение 11
Пусть, совокупность условий (26)
и (27)
выполняется для множества систем L
и только для них.
Тогда и только тогда говорят, что
Lявляется г е н е р а л ь н
о й
с о в о к у п н о с т ь ю о д н о р о д н ы х с и с т е м и пишут:
L= L(G)
и N(L) = N(L,G)
О величинах
Mj0(S,G) и Mj1(r,S,G); j = j0;
r = r0
говорят, что они являются о б ъ е к т и в н ы м и и н д и в и д у а л ь н ы м
и характеристиками нормального и
r–го ненормального
состояний j–ой
функциональной части системы S
Î L(G) соответственно.
О величине Mj0(S,G)
также говорят, что она является и н д и в и д у а л ь н о й
т о ч е ч н о й н о р м о й
j–го первичного показателя
состояния системы SÎ
L(G).
4. Область статистической нормы. Статистическая
точечная норма.
Обозначим через L0 подмножество
Lтакое, что
S Î L0 Û Mj1(S,G)
= Mj0(S,G) для всех j =
1..N(G) (28)
Определение 12
Пусть, условие (28)
выполняется для множества систем
L0 из
Lи только для них.
Тогда и только тогда говорят, что
L0 является
г е н е р а л ь н о й с о в о к у п н
о с т ь ю с и с т е м с
н о р м а л ь н ы м
с о с т о я н и е
м и пишут:
L0 = L0(G)
и N(L0) =
N(L0,G)
О величине
Mj0(G) =
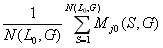
говорят, что она является с т а т и с т и ч е с к о й
т о ч е ч н о й
н о р м о й j–го
первичного показателя состояния системы S.
Если система S
является ТП множества систем
L, то имеет место:
Mj0(S,G)
= Mj0(G).
В общем случае, однако, выполняется условие
ú Mj0(S,G)
- Mj0(G)ú
≥ 0
Пусть
Bj(L0,G)
= {bjl 0;
j=1..N(L0,G)}
- генеральная совокупность возможных значений величины yj
для множества систем L0 ,
а Bj1
и Bj0
- непустые подмножества Bj1(S,G)
и Bj(L0,G)
соответственно:
Bjk = {bjl
k; j=
1..Njk}; k= 0,1
Обозначим
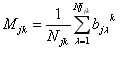
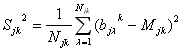
maxBjk
= max{bjl
k; j=
1..Njk} (29)
minBjk
= min{bjl
k; j=
1..Njk}
d jk=
Sjk
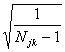
Определение 13
Пусть, совокупности
Bj= Bj0
+ Bj1; j
=1..N(G)
такие, что выполняются следующие условия.
1. Каждая Bj
представляет собой результаты равноточных и взаимно
независимых измерений величины yj.
2. Систематические ошибки измерений величины
yj
отсутствуют.
3. Случайные ошибки измерений величины
yjдля каждого k=
k0 (k0 =
0,1)
описывается стандартным нормальным распределением вероятностей, т.е. имеет
место:
D k(yj,G) =
0,
где
D k(yj,G)
– генеральное среднее арифметическое ошибок
измерений величины yj
для
k= k0 .
Если все эти три условия выполняются, то и м е е т с м ы с л
оперировать следующей совокупностью
неравенств:
ú Mj1 - Mj1(S,G)
ç < d
j1 tj1 и ú
Mj1 - Mj1(S,G) ç ≥
d j1 tj1
и (30)
ú Mj0 - Mj0(G)
ç < d
j0 tj0 и ú
Mj0 - Mj0(G) ç ≥
d j1 tj1
где
tjk–
критическое значение критерия Стьюдента при заданной вероятности
P= P0
и степени свободы Njk
– 1:
tjk= t(P,
Njk– 1) (31)
Обычно полагают, что
P= P0 ≥ 0.95
Вообще условия
ú Mj1
- Mj1(S,G)
ç < d
j1 tj1
и ú Mj0
- Mj0(G)
ç < d
j0 tj0
будут выполняться в том и только в том случае, когда
d jk
tjk> 0; k= 0,1;
j= 1..N(G)
(32)
Определение 14
Пусть, совокупности Bj1
и Bj0
такие,
что выполняется условие (32) и при этом имеют
место
ç Mj1
- Mj1(S,G)
ç < d
j1 tj1
при k= 1 ; j= j0;
j0 = 1..N(G)
и
ç Mj0
- Mj0(G)
ç < d
j0 tj0
при k= 1 ; j= j0;
j0 = 1..N(G)
Тогда и только тогда с доверительной
вероятностью P= P0
утверждают, что
1. Совокупность Bj1
является репрезентативной выборкой от
Bj1(S,G).
2. Совокупность Bj0
является репрезентативной выборкой от
Bj0(G).
В далее мы будем полагать, что
совокупности
Bjk;
k= 0,1; j= 1..N(G)
являются репрезентативными выборками от
соответствующих генеральных совокупностей.
Обозначим
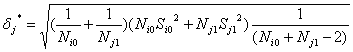 (33)
(33)
Пусть
tj* = t(P,
Nj0 + Nj1
– 2) (34)
- критическое значение критерия Стьюдента при заданной доверительной
вероятности Pи степени
свободы Nj0 +
Nj1 – 2.
В том случае, когда совокупность условий 1 – 3 выполняется
и при этом имеет место (32),
можно оперировать следующими противоположными
неравенствами [7]:
ç Mj1
- Mj0 ç
< d j*
tj* (35)
и
ç Mj1
- Mj0 ç
≥ d j*
tj* , (36)
где
d j*
tj* > 0 (37)
Определение 15
Пусть, совокупность условий 1 – 3
выполняется и при этом имеет место (32).
Пусть, далее
ú Mj1
- Mj1(S,G)
ç < d
j1 tj1
для всех j= 1..N(G)
ú Mj0
- Mj0(G)
ç < d
j0 tj0
для всех j= 1..N(G)
(38)
ç Mj1
- Mj0 ç
< d j*
tj* для всех j
= 1..N(G)
Тогда и только тогда с вероятностью
Pутверждают, что все
показатели состояния системы S
находятся в пределах общепринятой статистической
нормы.
О самой системе S
говорят, что она находится в н о р м а л ь н
о м с о с т о я н и и в
о б ы ч н о м с м ы с л е.
5. Область субъективной индивидуальной нормы.
Обозначим
A(d jk
, tjk) = [Mj0
- d jk
tjk , Mj0
+ d jk
tjk]; k= 0,1
и (39)
A(d j*,
tj*) = [Mj0
- d j*tj*
, Mj0 + d
j*tj*]
В том случае, когда имеет место
ç Mj0
- Mj0(G)
ç < d
j0 tj0
, (40)
с доверительной вероятностью P= P0
утверждают, что
Mj0(G)
= Mj0 .
На самом деле, однако, выполняется лишь условие
Mj0(G)
Î A(d
j0, tj0)
(41)
Аналогично, в том случае, когда
ç Mj1
- Mj0 ç
< d j*
tj*, (42)
с доверительной вероятностью P= P0
утверждают, что
Mj0(S,G)= Mj1(S,G) = Mj1
= Mj0 = Mj0(G)
(43)
Однако, в действительности,
т.е. объективно,
выполняются лишь следующие условия:
Mj0(G) Î A(d
j0, tj0) Ì A(d
j*, tj*) (44)
Mj0(S,G) Î A(d
j1, tj1) Ì A(d
j*, tj*) (44)
Mj1(S,G) Î A(d
j1, tj1) Ì A(d
j*, tj*), (46)
Как видно
ç Mj1 - Mj0
ç < d
j* tj* Þ
A(d j1, tj1)
Ì A(d j*,
tj*), (47)
Условие (44) выполняется по определению величины
Mj0(G)
и, следовательно, его выполнение никак не
зависит от того, выполняется ли условие (42).
При этом
Mj0(G) Î A(d
j*, tj*)
Û Mj0(S,G) Î A(d
j*, tj*)
Что касается условий (45) и (46),
то они выполняются в том и только в том
случае, когда выполняется условие (42). При этом имеет место
Mj1(S,G) = Mj0(S,G) ¹ Mj0(G)
при Mj1(S,G) Î A(d
j1, tj1) Ì A(d
j0 ,tj0) Ì A(d
j*,tj*)
и (48)
Mj1(S,G) = Mj0(S,G) = Mj0(G) при
Mj1(S,G) Î A(d
j1 , tj1) = A(d
j0 , tj0) Ì A(d
j*,tj*)
Чем обусловлена справедливость зависимости (48)?
Обозначим
D jmax=
max{D j0,
D j1,
D j*}
(49)
где
D jk =
d j0 tj0 ;
D j1 = d j1 tj1
и D j* =
d j*tj*
(50)
Казалось–бы, с помощью D
jmaxвеличина
yjможно измерять с точностью, которая
будет одинаково приемлемой всем: и тем, кто оперирует
зависимостью (40), и тем, кто оперирует зависимостью
ç Mj0
- Mj1(S,G)
ç < d
j1 tj1
, (51)
а также и тем, кто оперирует зависимостью (42).
В действительности, однако, дело обстоит
следующим образом.
Величина D j*,
согласно (33), (34)
и (50), определяется через четыре
переменных:
Sj1,
Sj0 , Nj1
и Nj0 .
В отличие от
D j*,
величина D
jk(k= 0,1), согласно
(29) и (31), определяется лишь через пару
величин Sjk, и
Njk.При этом, способ определения
величин D j0
и D
j1 является одним, а способ определения
D j*
является совершенно другим.
Все это говорит о следующем.
1. Понятия, обозначаемые через
D j1
и D
j0, являются между
собой с о п о с т а в и м ы м и, ибо эти понятия устанавливаются через о
д н и и т е ж е п р и з н а к о в и с помощью
о д н о г о и т о г о же способа.
2. Понятие, обозначаемое через
D j*,
по общности является сопоставым
с совокупностью понятий, обозначаемых через
D j1
и D
j0. Следовательно, это
понятие является б о л е е о б щ и м .
По этой причине совокупности
B(D j0)
и B(D
j1) являются
сопоставимыми между собой, но не являются сопоставимыми с совокупностью
B(D j*),
где
B(D jk)
– совокупность результатов обследования системы
S, установленная при
применении D jk.
в качестве единицы измерения величины yj;
B(D j*)
– совокупность результатов обследования системы
S, установленная при
применении D j*
в качестве единицы измерения величины
yj.
Из выше изложенного следует, что
зависимость (49) не является корректной; ею между собой сопоставляются
величины, обозначающие взаимно
несопоставимые понятия. Следовательно, величина D
jmax
не может служить в качестве единицы измерения yj
.
Отсюда необходимость введения следующей
величины.
Пусть, выполняется условие
Sj1 = Sj0
и Nj1 = Nj0
(52)
Согласно (29), (31), (33), (34) и (52),
имеют место
d j1
tj1 = d
j0 tj0
и d j*
tj* = d
0jt0j
(53)
где
d 0j=
Sj0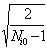 и t0j=
t(P, 2(Nj0
- 1)) (54)
и t0j=
t(P, 2(Nj0
- 1)) (54)
Обозначим
d 1j=
Sj1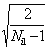 и t1j=
t(P, 2(Nj1
- 1)) (55)
и t1j=
t(P, 2(Nj1
- 1)) (55)
Согласно (29), (31), (33), (34), (54)
и (55), имеют
место
D jk0
< d 1j
t1j
< d 0j
t0j
< d j*
tj*
при Sj1 > Sj0
> 0 и 1 < Nj1 < Nj0
0 < d
j1 tj1
< d j0
tj0 при Sj1
> Sj0 > 0 и 1 < Nj1
< Nj0
0 < d 1j
t1j=
d 0j
t0j=
d j*
tj* при Sj1
= Sj0 > 0 и 1 < Nj1
= Nj0
0 < d
j1 tj1
= d j0
tj0 при Sj1
= Sj0 > 0 и 1 < Nj1
= Nj0
d 1j
t1j>
d j*
tj* > d
0jt0j
> 0 при Sj0 > Sj1
> 0 и 1 < Nj0 < Nj1
d j1
tj1 > d
j0 tj0
> 0 при Sj0 > Sj1
> 0 и 1 < Nj0 < Nj1
Эта совокупность зависимостей будет выполняться,
если положим, что вообще
0 < d 1j
t1j
< d 0j
t0j
< d j*
tj* Û 0
< d j1
tj1 <
d j0
tj0
0 < d 1j
t1j=
d 0j
t0j=
d j*
tj* Û 0
< d j1
tj1 = d
j0 tj0
(56)
d 1j
t1j>
d j*
tj* > d
0jt0j
> 0 Û d
j1 tj1
> d j0
tj0 > 0
Обозначим
A(d kj,tkj)
= [Mj0 - d
kj tkj,
Mj0 + d
kj tkj];
k= 0,1 (57)
Можно показать, что
Mj1(S,G) Î A(d
j*, tj*)
Û 0 <
d j1 tj1 ≤ d j0
tj0 < d j*,
tj* (58)
В самом деле, по определению A(d
j1,tj1)
имеет место
Mj1(S,G) Î A(d
j1,tj1) (59)
а из (29), (31), (55) и
(57) имеем
A(d j1,tj1)
Í A(d
1j, t1j)
(60)
Отсюда и из (59) получаем, что
Mj1(S,G) Î A(d
j1,tj1) Í A(d
1j, t1j)
При этом
Mj1(S,G) Î A(d
j*, tj*) при
A(d 1j, t1j)
Í A(d j*,
tj*)
и
Mj1(S,G) Ï A(d
j*, tj*) при
A(d 1j, t1j)
É A(d j*,
tj*) .
т.е. вообще
Mj1(S,G) Î A(d
j*, tj*)
Û A(d 1j,
t1j) Í A(d
j*, tj*) (61)
Согласно (39), (56) и (57)
имеет место
A(d 1j, t1j)
Í A(d j*,
tj*) Û
d j1,tj1 ≤
d j0,tj0 < d j*,
tj*
Отсюда и из (61)
имеем
Mj1(S,G) Î A(d
j*, tj*)
Û 0 <
d j1 tj1 ≤ d j0
tj0 < d j*,
tj* ,
т.е. получаем (58).
Согласно (46)
и (58) имеет
место
0 < d
j1 tj1
≤ d j0
tj0 < d
j*, tj*
(62)
Обозначим
d j=
d 0j
и tj=
t0jпри 0
< d j0
tj0 ≤ d
j1 tj1
и (63)
d j=
d 1j
и tj=
t1j
при 0 <
d j1
tj1 <
d j0
tj0 ,
Согласно (56), (62) и (63),
имеет место
0 < d
jtj≤ d
j* tj*
≤ d 0j
t0j(64)
Отсюда и из (50)
имеем
0 < D
j≤ D j*
≤ D 0j(65),
где
D j=
d j
tjи
D 0j=
d 0j
t0j, (66)
Величины D
jи
D 0j,
согласно (65),
являются минимально и максимально возможными значениями
D j* .
Следовательно, понятия, обозначаемые через
D j
и D
0j, являются ч а
с т н ы м и выражениями понятия, обозначаемого величиной D
j*. Это означает, что между
собой сопоставимыми являются следующие три
предположения.
Предположение 2
Все значения j–
го показателя от Mj0
- d j
tjдо Mj0
+ d j
tj являются друг от друга
практически неразличимыми.
Предположение 3
Все значения j–
го показателя от Mj0
- d j*
tj* до Mj0
+ d j*
tj*
являются друг от друга практически неразличимыми.
Предположение 4
Все значения j–
го показателя от Mj0
- d 0j
t0jдо
Mj+ d 0j
t0jявляются друг от
друга практически неразличимыми.
Из этих трех предположений наиболее
близким к истине, согласно (64),
является предположение 2..
А предположение 4,
согласно (64),
является наиболее отдаленным от истины.
Что касается предположения 3,
то оно, согласно (50), (65)
и (66),
является тем ближе к истине, чем величина D
j*
ближе к D j
. И, наоборот, чем величина
D j*
ближе к величине D
0j, тем
предположение 3 отдаленнее
от истины. Наиболее отдаленным
от истины предположение 3
является при D
j*= D 0j
. Это тот случай, когда предположение 3 неразличимо
от предположения 4.
Согласно (50), (65) и (66)
имеет место
D j*=
D 0j
Û d j*
tj* = d
0jt0j
или, с учетом (33), (34) и (54), окончательно
D j*=
D 0j
Û d j*
tj* = Sj1
= Sj0 и Nj1
= Nj0
Принимая во внимание это, приходим к следующему
выводу:
Предположения 3 и 4
являются друг от друга неразличимыми в том
и только в том случае, когда пара величин
Sj1 и
Nj1
служит характеристикой состояния типичного представителя множества систем
L0. А точнее,
когда имеет место
Mj1(S,G) = Mj0(S,G) = Mj0(G)
Î A(d j0 ,
tj0) = A(d j1 ,
tj1) Ì A(d
j*, tj*) (67)
Для величины Mj0(G),
как указывалось выше, условия (41)
и (44) выполняются по определению и,
следовательно, выполнение этих условии никак не
зависит от фактического состояния системы S.
При этом имеет место
Mj0(G) Î A(d
j0 , tj0) Û Mj0(G)
Î A(d j*,
tj*) (68)
Совокупность условий (41), (44), (67) и
(68) будет выполняться в том и только в том
случае, когда
Mj1(S,G)Î A(d
j1 , tj1) = A(d
j0, tj0) Ì A(d
j*, tj*)
Û Mj1(S,G) = Mj0(S,G) = Mj0(G)
Следовательно, в том случае, когда не выполняется условие
Mj1(S,G) Î A(d
j1 , tj1) = A(d
j0, tj0) Ì A(d
j*, tj*),
а выполняется условие
Mj1(S,G) Î A(d
j1 , tj1) Ì A(d
j0 , tj0) Ì A(d
j*, tj*),
должно иметь место
Mj1(S,G) = Mj0(S,G) ¹ Mj0(G)
Этим и обусловлена справедливость
зависимости (45).
Можно показать, что совокупность условий (45), (46)
и (48) будет
выполняться, если положим, что вообще
Mj1(S,G) = Mj0(S,G)
¹ Mj0(G) при Mj1(S,G)Î
A(d j , tj)
Ì A(d j*,
tj*)
и (69)
Mj1(S,G) = Mj0(S,G) = Mj0(G) при
Mj1(S,G)Î A(d
j , tj) = A(d j*,
tj*) ,
где
A(d j , tj)
= [Mj0 - d j tj , Mj0
+ d j tj ] (70)
В самом деле, согласно (56), (63) и (64),
имеет место
d j
tj <
d j*
tj* Û
d j1
tj1 <
d j0
tj0 <
d j*
tj
и
d j
tj = d
j* tj*
Û d j0
tj10 = d
j1 tj1
< d j*
tj *
и, следовательно, согласно (39) и (70),
A(d j , tj)
Ì A(d j*,
tj*) Û
A(d
j1 tj1) Ì A(d
j0 tj0) Ì (d
j* tj *)
и (71)
A(d j , tj) = A(d
j*, tj*)
Û A(d j0 tj10)
= A(d j1 tj1)
Ì (d j*
tj *)
Отсюда и из
(69) имеем
Mj1(S,G) = Mj0(S,G) ¹ Mj0(G)
при Mj1(S,G) Î A(d
j1 , tj1) Ì A(d
j1 , tj1) Ì A(d
j*, tj*)
и
Mj1(S,G) = Mj0(S,G) = Mj0(G) при
Mj1(S,G) Î A(d
j1 , tj1) = A(d
j0 , tj0) Ì A(d
j*, tj*),
т.е. получаем (48).
Кроме этого, согласно (69) и (71), имеют
место
Mj0(S,G) Î
A(d j , tj)
Ì A(d j*,
tj*)
и
Mj1(S,G)
Î A(d
j, tj)
Ì A(d
j*, tj*),
т.е. выполняются условия (45) и (46).
Согласно (69)
имеет место
Mj0(S,G)
Î A(d
j, tj)
(72)
Отсюда и из (70) имеем
Mj0(S,G) Î [Mj0
- d j tj , Mj0 +
d j tj ] (73)
или, с учетом (66),
Mj0(S,G)
Î [Mj0 -
D j,
Mj0 + D
j] (74)
Таким образом, точечная индивидуальная норма
Mj0(S,G)
всегда находится в пределах области
[Mj0 -
D j,
Mj0 + D
j].
Отсюда следующее предположение.
Предположение 5
Все значения j–
го показателя
от Mj0 -
D jдо Mj
+ D jявляются друг
от друга практически неразличимыми.
Согласно (65)
имеет место
0 < D
j≤ D 0j
(75)
Следовательно, предположение 5
тем ближе к
истине, чем величина D j
близка к нулю. И, наоборот, это
предположение является тем отдаленнее от истины,
чем величина D j
ближе к
D 0j=
d 0j
t0j. Предположение 5
самым отдаленным от истины, согласно (75),
будет при D
j= D 0j
= d 0j
t0j.
Но в этом случае, как мы знаем, выполняются
следующие условия.
Предположение 5 неразличимо
от предположения 3.
В качестве точечной нормы Mj0(S,G)
служит статистическая точечная норма
Mj0(G),
т.е. имеет место
Mj0(S,G)
= Mj0(G),
Определение 16
Пусть, имеют место (72) и, следовательно,
согласно (39), (57), (64)
и (70),
выполняется условие
Mj0(S,G) Î A(d
j,tj ) Í A(d
j*,tj *) Í
A(d 0j,t0j )
Тогда и только тогда с вероятностью P≥ 0.95
утверждают, что
1. Множество A(d
j,tj)
является о б л а с т ь ю и н д и в и д у а л ь н о
й н о р м ы j–го
первичного показателя состояния системы S.
2.Имеет место
Mj0(S,G) = Mj1(S,G) при Mj1(S,G)
Î A(d j, tj)
и (76)
Mj0(S,G) = Mj0(G) при Mj1(S,G)
Ï A(d j, tj)
3. Величина
D j=
d j
tj(77)
является л о к а л ь н о й минимально- возможной е д и н и ц е й измерения
yjв системе S.
Если
Mj1(S,G)
Î A(d
j, tj),
то
÷ Mj1(S,G) - Mj0(G)÷
³ ÷ Mj1(S,G) -
Mj0(S,G)÷ ³ 0
При этом, в том случае, когда
Mj1(S,G) - Mj0(G)÷ =÷
Mj1(S,G) - Mj0(S,G)÷ = 0,
имеют место
Mj1(S,G) = Mj0(S,G) = Mj0(G)
и
D j1 =
D j0
и D 1j
= D 0j
А в этом случае предположение 4, как было
показано выше, является наиболее отдаленным
от истины.
Если
Mj1(S,G) Ï A(d
j, tj),
то
÷ Mj1(S,G) - Mj0(G)÷
>÷ Mj1(S,G) - Mj0(S,G)÷
> 0
и
D j1
>D j0
и D 1j
>D 0j
= D j
Следовательно, в этом случае предположение 4 всегда будет наиболее отдаленным
от истины.
Отсюда смысл той части зависимости (76),
где выполняется условие
Mj0(S,G) = Mj0(G) при
Mj1(S,G) Ï A(d
j, tj)
Таким образом, точечная индивидуальная норма Mj0(S,G)
от точечной статистической нормы
Mj0(G)
отличается т о л ь к о в т о м с л у ч а е,
когда
D j
< D 0j
,
что вполне логично.
Величину D j,
согласно (54), (55), (63)
и (77),
устанавливают путем совместной обработки лишь одних данных
Sj1 и Nj1;
j= j0
Следовательно, на величине D
jникак не
сказываются данные
Sjkи
Njk; k= 0,1;
j= 1..N(G);
j¹ j0
.
Отсюда смысл выражения: «Величина D
jявляется
локальной единицей»
Область индивидуальной нормы
A(d j,tj),
согласно (54), (55), (63)
и (70),
определяется совокупностью данных
P, Mj0,
Sj1 и Nj1;
j= j0 (78)
Величина P, как известно,
задается специалистом. К тому же при одной P
совокупность данных
Mj0 , Sj1
и Nj1; j=
j0
является одной, при другой P–
другой и т.д. По этой причине произведение
d j
tj, согласно
(54), (53) и (63), при одной вероятности P
является одной, при другой вероятности
P– другой и т.д.
В итоге, область индивидуальной нормы
A(d j,tj),
так и область статистической нормы
A(d j0,tj0),
является с у б ъ е к т и в н о й характеристикой
j–ой функциональной
части системы S. А
величина D jmin
= d j
tjявляется с у б
ъ е к т и в н о й локальной минимально–возможной ошибкой измерения
yjв системе S.
6. Область объективной индивидуальной нормы.
Кванты различимости
функциональных частей системы
Пусть
d j(S,G)
и tj(S,G)
– значения d
jи tj
такие, что
d j = d
j(S,G) и tj(S,G) = tj
при Bj1 = Bj1(S,G) (79)
Обозначим
A(d j(S,G), tj(S,G))
= [Mj0(S,G) - d j(S,G) tj(S,G),
Mj0(S,G) + d j(S,G) tj(S,G)]
(80)
Область A(d
j(S,G),
tj(S,G)),
в отличие от области A(d
j,tj),
для системы S,
согласно (79),
является вполне определенной. Можно говорить, что она является о б ъ е к
т и в н о й
и н д и в и д у а л ь н о й н о р м о й j–го
первичного показателя состояния системы S.
Обозначим
D *(j,S,G) = d
j(S,G) tj(S,G) (81)
Величина D *(j,S,G),
в отличие от D
j, для системы S,
согласно (79) и
(81), является вполне определенной.
Определение 17
Пусть, имеют место (79)
и (81).
Тогда и только тогда об области
A(d j(S,G),
tj(S,G))
говорят, что она является
о б ъ е к т и в н о й и н д и в и д у а л ь н о й н о р м о й
j–го первичного показателя состояния
системы S.
О величине D j(S,G)
говорят, что
она является о б ъ е к т и в н о й л о к а л ь н о й минимально-
возможной е д и н и ц е й и з м е р е н и я величины yj
в системе S
и пишут:
D j(j,S,G) = D
*(j,S,G), (82)
где
D j(j,S,G)
– единица измерения величины yjв
j–ой функциональной части системы S.
О величине D j
говорят, что оно является с у б ъ к т и в н о й
локальной минимально- возможной единицей измерения величины
yjв системе
S.
Согласно (81) и (82) имеет место
D (j,S,G) = d j(S,G)
tj(S,G) (83)
Можно говорить, что величина D
j(S,G)
является к в а н т о м р а з л и ч и м о с т и
состояний j–ой
функциональной части системы S.
Соответственно о величине D
jможно
говорить, что она является о ц е н к о й
кванта различимости D (j,S,G)
при заданной доверительной вероятности
P.
7. Объективная предельная относительная ошибка
измерения
первичных показателей состояния системы
Обозначим
a (j,S,G)
= 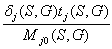 (84)
(84)
Можно показать, что
0 < a (j,S,G)
= ≤ 0.5 (85)
В самом деле, по определению целостной системы
каждый ее первичный показатель yj
имеет три или более друг от друга
различаемых значений.
Пусть, m(j,S,G)
– количество возможных значений величины
yjобъективно
друг от друга различаемых в системе S
в данный момент времени:
m(j,S,G)
³ 3
Принимая во внимание, что D
(j,S,G)
является объективной минимально-возможной единицей измерения величины
yjв системе
S, можно написать,
что
yj Î {yjk ; k = 1.. m(j,S,G)},
где
yjk = k D (j,S,G)
При этом
Mj0(S,G) = 2 D (j,S,G) при
m(j,S,G) = 3
и (86)
Mj0(S,G) ³ 2 D
(j,S,G) при m(j,S,G) > 3,
Справедливость зависимости
Mj0(S,G) = 2 D (j,S,G) при
m(j,S,G) = 3
следует из определения величины Mj0(S,G).
В самом деле, в том случае, когда
m(j,S,G)
= 3, величина yj2
= 2 D (j,S,G)
является значением yj,
о д и н а к о в о о т д а л е н н ы м как от
yj1 = D
(j,S,G),
так и от yj3
=
3 D (j,S,G).
В виду этого, величина yj
из значения yj1
в значение yj3
или, наоборот, из значения yj3
в значение yj1
может перейти, только пройдя значение
yj2 = 2 D
(j,S,G).
Следовательно, величина yj2
= 2 D (j,S,G)
является о б ъ е к т и в н о н а и б о л е е
ч а с т о в с т р е ч а е м ы м - н о р м а л ь н ы м -
значением yj
, т.е. имеет место
yj2 = 2 D (j,S,G) = Mj0(S,G)
при m(j,S,G) = 3
Согласно (85) имеет место
Mj0(S,G)
³ 2 D (j,S,G)
> 0 (87)
Отсюда и из (83) и (84) имеем
0 < a (j,S,G)
= ≤ 0.5,
т.е. получаем (85).
Величина Mj0(S,G)
для каждой системы S
является вполне определенной, т.е. имеет место
Mj0(S,G) = Mj0(S0,G) при
S = S0 (88)
где
Mj0(S0,G)
– фиксированное значение Mj0(S,G).
С учетом (88) из (83) и (84) получаем
a (j,S,G)
® 0 Û
D (j,S,G)
® 0 (89)
Совокупность условий (8), (9), (85) и (89) будет
выполняться, если положим, что вообще
P(j,S,G)
= 1 - a (j,S,G)
(90)
Определение 18
Пусть, имеют место (85), (89) и (90).
Тогда и только тогда говорят, что величина
a (j,S,G)
является объективной предельной относительной
ошибкой измерения величины yj
в системе S:
Согласно (11) и (90) имеют место
P(O,S,G) = 1 - max{a (j,S,G);
j=
1..N(S,G)}
и (91)
P(Z,S,G) = 1 - min{a (j,S,G);
j=
1..N(S,G)}
8. Оценка точечной
индивидуальной нормы.
Величины Mj1(S,G)
и Mj0(G),
как правило, являются неизвестными. По этой
причине, величина Mj0(S,G),
согласно (76),
как правило, тоже является неизвестной.
Обозначим
MZj= Mj1,
если Mj1
Î A(d
j, tj)
и (92)
MZj= Mj0,
если Mj1
Ï A(d
j, tj)
Сопоставляя между собой зависимости (76)
и (92), можно с
вероятностью P
утверждать, что величина MZj
представляет собой о ц е н к у
Mj0(S,G).
Согласно (29), (31) и (32)
должны иметь место
Sjk> 0 и
Njk> 1; k= 0,1;
j= j0
Вообще
P> 0, Sj0
> 0 и Nj0 >> 1; j
= j0 (93)
Благодаря
этому для определения величин d
j0 и
tj0 ,
по-прежнему, можно оперировать зависимостями
d j0 =
Sj0
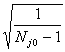 и tj0
= t(P, Nj0
-1) (94)
и tj0
= t(P, Nj0
-1) (94)
Что касается
условия
Sj1 > 0
и Nj1
> 1; j= j0 ,
то оно в общем случае не выполняется. Оно не выполняется, например, при
первом обследовании состояния системы S,
когда Nj1
= 1 и, следовательно, согласно (29),
имеет место: Sj1
= 0.
Отсюда необходимость рассмотрения самого общего
случая, когда
Sj1 ≥ 0 и Nj1
≥ 1
и внесения соответствующего уточнения в способы
определения величин d j1
и tj1.
Эти величины в
далее мы будем устанавливать с помощью соотношений
d j1 =
Sj1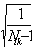 при Sj1 > 0
и Nj1
> 1
при Sj1 > 0
и Nj1
> 1
и (95)
d j1 =
d j0 при
Sj1 = 0 или Nj1
= 1
tj1 = t(P,
Nj1 -1) при Nj1
> 1
и (96)
tj1 = tj0
при Nj1 = 1
К чему это приводит?
Пусть, не выполняется условие
Sj1 > 0 и Nj1
> 1 (97)
и, следовательно, согласно (95) и (96),
имеет место
d j1
tj1 = d
j0 tj0
(98)
Отсюда и из (93) и (94)
имеем
d jk
tjk> 0 ; k=0,1,
т.е. выполняется условие (31).
Вместе с тем, в том случае,
когда выполняется условие (98),
из (56) получаем, что
d j
tj= d 0j
t0j
Отсюда и из (66) имеем
D j=
D 0j.
В итоге, предположение 1 становится неразличимое
от предположения 3. А это означает, что в том случае, когда условие (97)
не выполняется,
и с т и н а м о ж е т б ы т ь
у с т а н о в л е н а лишь той точностью, с какою это вообще возможно с
применением величины Mj0
в качестве MZj.
Такая точность, как указывалось выше, является
совершенно достаточной, когда
выполняется условие (36).
Как обстоит дело в том случае, когда
выполняется условие (35) ?.
Вообще, согласно (39), (56) и (63)
имеет место
Mj1Î A(d
j, tj) Û
Mj1Î
A(d j1, tj1)
Í A(d j0, tj0)
Û
d
j1, tj1
≤ d j0, tj0 (99)
С учетом этого зависимость (92) можно переписать
в виде
MZj= Mj1,
если d
j1, tj1
≤ d j0,
tj0
и (100)
MZj= Mj0,
если d
j1, tj1
> d j0,
tj0
В том случае, когда выполняется условие (35), с
доверительной вероятностью P³
0.95 утверждают, что
Mj1 = Mj0 Î A(d
j1, tj1) Í A(d
j0, tj0) (101)
С учетом (101) из (98), (99) и (100) получаем
MZj= Mj1
= Mj0
Таким образом, в том случае, когда условие (97)
не выполняется, всегда имеет место
MZj= Mj0,
т.е. в качестве индивидуальной нормы служит величина Mj0.
Итак, введение зависимостей (95) и (96) приводит
к тому, что
1. Условие (32)
выполняется всегда, когда выполняется
условие (93).
2. Состояние j–ой
функциональной части системы S
всегда можно оценить, по крайней мере, с той
точностью, с какою это вообще возможно с применением величины Mj0
в качестве MZj.
9.Объективные и субъективные внутрисистемные
единицы измерений
Пусть, POи
PZ- значения
P(O,S,G)
и P(Z,S,G),
такие что
PO = P(O,S,G) Û Bj1 = Bj1(S,G)
для всех j = 1..N(S,G)
и (102)
PZ = P(Z,S,G) Û Bj1 = Bj0(S,G)
для всех j = 1..N(S,G)
Обозначим
D j(O) = (1 – P(O)) Mj(Z)
и D j(Z) = (1 – P(Z))
Mj(Z) (103)
Определение 19
Пусть, имеют место зависимости (102)
и (103).
Тогда и только тогда с вероятностью
P³ 0.95 утверждают, что
1.Величины POи
PZслужат о ц е н к а м и
P(O,S,G)
и P(Z,S,G)
соответственно.
2.Величина D
j(O)
является ф а к т и ч е с к о й е д и н и ц е й и з
м е р е н и я величины yj
в системе S.
3. Величина D
j(Z)
является н о м и н а л ь н о й е д и н и ц е й и з
м е р е н и я величины yj
в системе S:
D j(O)
= D j(Z)
при P(O) = P(Z)
Говорят также, что величина
PZявляется с у б ъ е к т и
в н ы м в е р о я т н о ст н ы м п р е д е л о м п о з н а н и я истины в
системе S.
Пусть
D j(O,S,G) и
D j(Z,S,G)
- значения
D j(O)
и D j(Z)
такие, что
D j(O) = D
j(O,S,G) при Bj1 = Bj1(S,G)
для всех j = 1..N(S,G)
и (104)
D j(Z) = D
j(Z,S,G) при Bj1 = Bj0(S,G)
для всех j = 1..N(G)
О величине D j(O,S,G)
говорят, что она является о б ъ е к т и в н о й ф а
к т и ч е с к о й е д и н и ц е й и з м е р е н и я величины
yjв системе
S.
О величине D
j(Z,S,G)
говорят, что она является о б ъ е к т и в н о й н о
м и н а л ь н о й е д и н и ц е й и з м е р е н и я величины
yjв системе
S:
D j(O,S,G) = D
j(Z,S,G) при P(O,S,G) = P(Z,S,G).
О величинах D j(O)
и D
j(Z)
можно говорить,
что они являются о ц е н к а м и D
j(O,S,G)
и D
j(Z,S,G)
соответственно при заданной доверительной вероятности P.
Говорят также, что величины
D j(O)
и D
j(Z)
представляют собой внутрисистемные - фактическую и
номинальную - единицы измерения
yj.
Можно показать, что вероятность
P(S,G)
является д и с к р е т н о й величиной [ ].
В самом деле, согласно (91),
имеет место
P(S,G) = 1 – min{a j(S,G);
j = 1.. N(S,G)}, (105)
Следовательно, для того, чтобы P(S,G)
была дискретной величиной достаточно, чтобы, по
крайней мере, дискретной была величина:
min{a j(S,G); j = 1..
N(S,G)
Покажем, что все величины
a j(S,G)
; j= 1.. N(S,G)
(106)
являются дискретными величинами.
В самом деле, каждая из величин (106) является
объективной характеристикой системы S.
А точнее, имеет место:
a j(S,G) = a
j(S0,G) при S = S0
Î L, (107)
где
a j(S0,G)
– фиксированное значение a
j(S,G).
Множество L
по определению представляет собой генеральную
совокупность систем
о д н о г о и т о г о ж е ф у н к ц и о н а л ь н о г о назначения. При этом,
для этого
множества Lимеет место
N(L) <
¥ ,
т.е. оно является к о н е ч н ы м множеством.
Следовательно, согласно (107), конечным
является и множество возможных значений переменной a
j(S,G).
Любая переменная, с конечным множеством
возможных значений, как известно, является д и с к р е т н о й величиной.
Таким образом, переменная a
j(S,G).является
дискретной величиной. Следовательно, согласно (105), дискретной является
и величина P(S,G).
10 Субъективный вероятностный предел познания истины
Обозначим
a j=
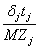 ,
если
,
если
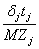 ≤ 0.5
≤ 0.5
и (108)
a j= 0.5 ,
если
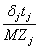 > 0.5
> 0.5
Согласно (108)
имеет место
0 < a j≤ 0.5
(109)
Для величинMZj
, d j
и tj
выполняются условия
MZj = Mj0(S,G) Û Bj1
= Bj1(S,G)
d j = d
j(S,G) Û Bj1 = Bj1(S,G)
(110)
tj = tj(S,G) Û Bj1
= Bj1(S,G)
Согласно (84), (108) и (110)
имеет место
a j =
a j(S,G) Û Bj1
= Bj1(S,G)
Следовательно, можно говорить, что a
jявляется
о ц е н к о й величины a
j(S,G).
Можно показать что, величины
a j;
j= 1..N(S,G),
(111)
в отличие от величин
a j(S,G);
j= 1..N(S,G),
(112)
н е о б я з а т е л ь н о являются дискретными величинами.
В самом деле, как указывалось выше,
выборка Bj1
при одной доверительной вероятности
P, является одной, при
другой вероятности P–
другой и т.д.
Следовательно, величина a
j,
согласно (108) и (110),
является зависимой от P.
Величина P,
как известно, является непрерывной величиной.
Следовательно, и величина a
j, как зависящая от
P, должна являться
непрерывной. По крайней мере, в общем случае мы не можем утверждать, что
величина a j
обязательно являются дискретной величиной.
Обозначим
hZ= min{a
j; j= 1..N(S,G)}
NZ= 1 + round(
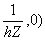 (113)
(113)
PZ* = 1 -
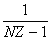
Согласно (113) имеет место
PZ* = f(a
j; j= 1..N(S,G))
(114)
При этом величина PZ*,
как и величина P(S,G),
является дискретной величиной. Более того,
согласно (108), (110) и (113), имеет место
hZ = 1 – min{a j(S,G); j = 1.. N(S,G)}
Û
Bj1 = Bj0(S,G) (115)
А согласно (108), (110) и (114) имеем
PZ* = f(a j(S,G) ; j = 1..N(S,G))
Û Bj1 = Bj0(S,G) (116)
Совокупность условий (113), (115) и (116)
будет выполняться, если положим, что вообще
PZ* = P(S,G) Û Bj1 = Bj0(S,G)
для всех j = 1..N(S,G)
Отсюда и из (102) имеем
PZ= PZ*
(117)
С учетом (117) из (113) получаем,
PZ= 1 -
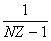 (118)
(118)
Определение 20
Пусть, имеет место (113)
и, следовательно, выполняется условие (118).
Тогда и только тогда с вероятностью
P³ 0.95
утверждают, что величина PZ
служит о ц е н к о й P(S,G).
О величине PZ
говорят также, что она является субъективным
вероятностным пределом познания истины в системе
S.
Полный алгоритм определения
PZопубликован в [8]
и [9]. А в целом настоящая статья приложена
к [10] под названием «Математическое обоснование способа для определения
индивидуальных норм».
З а к л ю ч е н и е
1. Общепринятая статистическая норма
A(d j*
, tj*) = [Mj0 - d
j* tj*, Mj0 +
d j* tj*]
представляет собой множество значений величины Mj1
, для которых имеет место
ç Mj1
- Mj0 ç
< d j*
tj* , (1)
где Mj0
такое, что выполняется условие
ú Mj0
- Mj0(G)
ç < d
j0 tj0
(2)
Индивидуальную норму
A(d j, tj) = [Mj0
- d j tj, Mj0 +
d j tj]
составляют значения величины Mj1
, для которых, кроме (1) и (2), также выполняется
условие
ú Mj1
- Mj1(S,G)
ç < d
j1 tj1
(3)
Это дополнительное ограничение приводит к тому, что область A(d
j, tj)
в с е г д а является п о д о б л а с т ь ю
A(d j*
, tj*)
и, следовательно, выполняются условия
Mj0(S,G)
Î A(d
j, tj)
Í A(d
j* , tj*)
и Mj0(G)
Î A(d
j* , tj*).
Соответственно выполняются и условия
MZjÎ
A(d j,
tj) Í
A(d j*
, tj*) и Mj0
Î A(d
j* , tj*).
(4)
Из совокупности зависимостей (4) видно, что область возможных значений
величины MZjявляется более определенной, т.е.
к о н к р е т н о й, чем область возможных значений величины Mj0
. А благодаря этому величина
MZjпри заданной доверительной вероятности
P≥ 0.95 служит более
определенной – к о н к р е т н о й, т о ч н о й – характеристикой нормального
состояния системы S,
чем величина Mj0 .
2. Системой неравенств (1), (2) и (3) можно
оперировать, если выполняются следующие условия:
Условие 1
Каждая выборка Bj
= Bj1 + Bj0
представляет собой результаты равноточных и взаимно
независимых измерений величины yj
Условие 2
Систематические ошибки измерений величины
yjотсутствуют, а
случайные ошибки ее измерений описывается нормальным распределением
вероятностей.
Условие 3
Имеет место
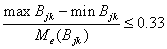 для всех
j= 1..N(G);
k= 0,1,
для всех
j= 1..N(G);
k= 0,1,
где Me(Bjk)
- медиана выборки Bjk
.
Условие 4.
Выборки Bj1
и Bj0
являются репрезентативными с доверительной
вероятностью P≥ 0.95.
Все эти условия,
как видно, являются самыми естественными, и
их выполнение требуется всюду как в живой, так и не живой природе.
Следовательно, индивидуальная точечная норма
Mj0(S,G),
как естественный глобальный оптимум, должна служить
объективной характеристикой нормального состояния широкого класса систем живой и
не живой природы.
Цитированная литература
1. Хускивадзе А.А., Хускивадзе А.П. Вероятностный предел познания истины и
вопросы математического моделирования живого организма как единого целого.
http://www.medlinks.ru/artikle.php?sid=32701
2. Игамбердиев А.У. Логика организации живых
систем. – Воронеж. – Изд. ВГУ – 1995. - 152 с.
3.Категории диалектики и принципы целостности.
/Гурвич С.С. //Сб. ,, Философские проблемы медицины,, - Киев – Здоровье - 1969.
- 54-73 с.
4. Хускивадзе А. П. Целостные системы, -
Тбилиси . – Изд. « Сабчота Сакартвело» . - 1979. с
5. Хускивадзе А.П. Задачи многокритериальной
оптимизации и оценивания в эмирических целостных системах и их решения. –
Тбилиси: - Изд. ,,Сакартвело,, , - 1991, -118 с.
6. Хускивадзе А.П., Хускивадзе А.А. Способ определения степени здоровья
человека.
Патент Российской Федерации. RU2141791
C1, кл.
A61 B10/00, 1999.
7. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М. –
Наука.
Главная редакция физико-математической литературы. - 1983. – 416 с.
8. Хускивадзе А.А, Хускивадзе А.П. Определение
степени переносимости организмом человека врачебных и других воздействий.
RU2007.110.568. А. 2007. Бюл. 23
9. Определение степени переносимости организмом
больного с пневмонией активной ортостатической пробы. RU
2007120810 А 2007.
Бюл. 33
10. Определение степени переносимости
организмом больного тревожно-депрессивными расстройствами
врачебных и других воздействий
RU2007140016 A. 2008.
Бюл. 13.
Адрес для переписки:
396901, Воронежская обл., г. Семилуки, ул. 9-го
января, 19, кв. 7. А.П.Хускивадзе
Тел.: 8-(4-73-72)-2-30-93
Сведения об авторах:
1. Хускивадзе Амиран Амиранович –
Doсtorof
philosophy, работал в
областях ядерной, атомной и молекулярной физики, а также и в доказательной
медицине. Его статьи публиковались в таких журналах по физике, как “Journal
ofPhysicsB:
Atomic, Molecular
andOpticalPhysics” и “Physics
review”.
2. Хускивадзе Амиран Пименович –
Физик-кибернетик, в 1970 – 1985 годы руководил различными лабораториями Отдела
медицинской кибернетики НИИ Экспериментальной и клинической хирургии МЗ
Грузинской ССР. С 1985 по 1997 годы заведовал Отделом медицинской системотехники
НИИ Экспериментальной и клинической терапии МЗ Грузинской ССР. В настоящее время
находится на пенсии. Имеет 55 научных публикаций в областях общей теории систем
и доказательной медицины.

