
Гл. 6. Естественный глобальный оптимум
6.1. Постановка задачи
Исследованием глобального оптимума мы начали
заниматься еще в конце семидесятых годов под руководством доктора физико –
математических наук профессора МГУ В.Б. Кудрявцева. Позже нам пришлось сузить
область исследования: ограничившись изучением т.н. естественного глобального
оптимума.
Понятие «Естественный глобальный оптимум»
впервые мы применили в работах [16, 17]. Под этим нами понимается глобальный
оптимум, сформированный естественным образом в результате пересечения большого
числа случайных и неслучайных процессов, происходящих в природе. Естественным
глобальным оптимумом (ЕГО) является, например, индивидуальная норма человека.
Способ определения ЕГО, приведенный в работах
[16, 17], предполагает, что являются известными как данные
Bj1(s) = {bjl
1(s) ; l = 1..Nj1(s)};
j = 1..n, s = 1..m (6.1)
так и данные
Bj0(s) =
{bjl 0;
l = 1..Nj0(s)};
j = 1..n, (6.2)
где
Bj1(s)
– выборка результатов обследования показателя
yj Î
Y у МР
sÎ S Í
S;
Y– генеральная
совокупность первичных показателей состояния МР S;
n – объем
Y: n ≥2 ;
m – количество
анатомических элементов МР S: m≥2;
Bj0 –
выборка результатов обследования показателя
yj Î
Y у множества МР
S0 Í
S;
S0 –подмножество
анатомических элементов МР S,
находящихся в нормальном состоянии.
Здесь под первичными показателями состояния МР
S понимаются
количественные величины, которые
1) служат общими
характеристиками состояния МР
S,
2) установлены непосредственно путем
измерения с помощью единого способа для всех
анатомических элементов МР S.
Предполагается также, что совокупности (6.1) и
(6.2) с вероятностью P* ( 0.95 ≤
P*< 1) служат
репрезентативными выборками из генеральных совокупностей
Bjk(G);
j = 1..n (6.3)
и, следовательно, имеют место
Njk
>>1 ; k = 0,1; j = 1..n
К сожалению, часто неизвестными являются не
только совокупности (6.3), но даже и совокупности (6.1) и (6.2).
Вообще с самого начала неизвестными являются как
совокупности (6.1), так и совокупности (6.2).
Однако, в случаях, когда необходимо судить о состоянии МР
S, обойтись без знания этих
совокупностей - просто невозможно. Прежде всего, специалисты вынуждены
всегда собирать данные (6.1).
Возникает вопрос: зная данные
Bj1(s) = {bjl
1(s) ; l = 1..Nj1(s)};
j = 1..n; s = 1..m, (6.4)
нельзя ли установить совокупность величин
Mj0(s),
Sj0(s)
и Nj0(s);
j = 1..n; s
= 1..m (6.5)
которые служили бы объективными эталонами нормального состояния –
индивидуальными нормами - анатомических элементов МР
S ?
Ниже мы увидим, что это вполне возможно.
6.2. Метод измерения с наибольшей точностью
Согласно второму закону гармонии в каждой
целостной системе S
выполняется условие равно точности
измерений. Отсюда смысл требования, которое предъявляется каждой выборке
Bj1 = {Bj1(s);
j = 1..n}
Она должна быть составлена результатами равноточных измерений, т.е. должно
иметь место [22]:
D j(s)
= D j(0)
для всех j = 1..n
и s = 1..M,
(6.6)
где
D j(s)
– единица измерения величины
yjÎ Y,
фактически используемая в МР s (s = 0..
m) при
t = t0.
Согласно (3.1) и (4.28) имеет место
D j(s)
= (1 – p) Mj0(s);
j = 1..n; s
= 0..m
При этом, вообще имеет место
D j(s)
≥ D j(п,s)
≥ s j(s);
j = 1..n; s
= 0..m, (6.7)
где
D j(п,s)
– абсолютная ошибка «измерительного прибора», с
помощью которого при t = t0
величина yjÎ
Y в МР s
= 0 фактически измеряется.
s j(s)
– генеральное среднеквадратическое отклонение
измерений величины yjÎ
Y в МР s.
Величина s
j(s),
как правило, является неизвестной. Поэтому на
практике, как было указано в главе 4, всегда оперируют величиной:
D j(s)
= 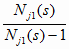 Sj1(s),
(6.8) Sj1(s),
(6.8)
где
D j(s)
– «исправленное среднеквадратическое отклонение
измерений величины yjÎ
Y в МР s
при t =
t0:
D j(s) →
s j(s)
при Nj1(s)
→ ∞
В итоге, условие (6.6) будет выполняться в том и
только в том случае, когда
D j(s)
= D j(0) ≥
D j(0) =
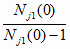 Sj1(0)
для всех j = 1..n
и s = 1..m,
(6.9)
Sj1(0)
для всех j = 1..n
и s = 1..m,
(6.9)
где, согласно (2.11),
Sj1(0) =
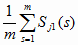 и Nj1(0)
=
и Nj1(0)
= 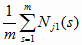 (6.10) (6.10)
Согласно третьему закону гармонии для каждой
целостной системы S
величина P имеет
свой, вполне определенный, верхний предел P0
[3, 4]. Этот предел таков что, равенство
P = P0 (6 11)
выполняется тогда и только тогда, когда система S
находится в нормальном состоянии
и, следовательно, имеют место:
P = P0 Þ Mj0(s)
= Mj0(0); Sj0(s) = Sj0(0)
и Nj0(s) = Nj0(0)
для всех j
= 1..n и
s = 0..m
и (6.12)
P = P0
Þ D j(s)
= D j0
для всех j = 1..n
и s = 1..m,
где
D j0 –
минимально возможное значение величины
D j(s)
для системы S
при t =
t0:
Согласно (6.9) имеет место
D j(s)
= D j0
Û D j(s)
= 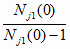 Sj1(0); j =
1..n; s = 1..m,
Sj1(0); j =
1..n; s = 1..m,
т.е. вообще
D j0 =
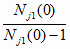 Sj1(0); j =
1..n (6.13)
Sj1(0); j =
1..n (6.13)
Отсюда смысл следующего положения.
Определение 6.1.
Пусть, имеет место (6.1) и, следовательно,
согласно (6.6), (6.12) и (6.13), выполняется условие
D j(s)
= D j0 =
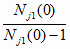 Sj1(0)
Sj1(0)
для всех j = 1..n
и s = 1..m
(6.14)
Тогда и только тогда говорят, что в системе
S измерение величины
yj Î
Y производится наиболее
точно, и пишут:
D j(s) =
D j0 = Sj0
для
всех j = 1..n; s = 1..m
(6.15)
Согласно (6.14) и (6.15) имеет место
Sj0 =
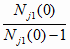 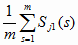 ;
j = 1..n (6.16) ;
j = 1..n (6.16)
Итак, оперируя данными
Sj1(s)
и Nj1(s);
j = 1..n; s
= 1..m,
с помощью совокупности соотношений (6.10) и (6.16) всегда можно найти
величины
Sj0; j =
1..n, (6.17)
служащие характеристиками нормального состояния ТП анатомических элементов ЦС
S при
t = t0
6.3.Определение точечных статистических норм
Каждая
МР s, согласно
первому закону гармонии, является целостной системой с вероятностью
p(s) (0.5 ≤ p(s)
< 1), а каждая ее j
ая функциональная часть, со своей стороны, является
целостной системой с вероятностью pj(s)
(0.5 ≤ p(s) < 1).
При этом, согласно следствию второго закона
гармонии вероятность целостности МР s
равна вероятности ее самого слабого звена, т.е.
имеет место
p(s) = pj; j = j0; j0 =
1..n, (6.18)
где
pj = min(pj(s); s = 1..m), (6.19)
В
итоге
p(s) = P Û pj = P; j = j0; j0
= 1..n (6.20)
где
P – вероятность фактического
познания истины в системе S при t = t0.
Обозначим
hj = min{hj(s); s = 1..M], (6.21)
где
hj(s) = 1 -
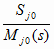 (6.22)
(6.22)
Согласно (4.48)
и (6.22) имеет место
h(s) = h
Û pj =
P для всех
j = 1..n
и s = 1..m
(6.23)
Для величин h
и P,
согласно (4.49),
имеет место:
h = 1 -
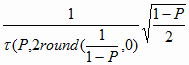 , (6.24) , (6.24)
где
t ( P, 2
round(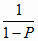 ,0))
(6.25) ,0))
(6.25)
– критическое значение критерия Стьюдента при
заданной вероятности P
и степени свободы 2 round(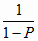 ,0). ,0).
Из (6.23) и (6.24) имеем
hj = h
Û pj =
P; j = j0;
j0 = 1..n (6.26)
Пусть, система S
находится в нормальном состоянии и, следовательно,
имеет место
pj = P0
для всех j = 1..n
Отсюда и из (4.45), (4.49) и
(6.26) имеем
hj = h0
для всех j = 1..n
(6.27)
и, в конечном счете, согласно (4.46),
Mj0 =
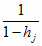 Sj0;
j = 1..n (6.28) Sj0;
j = 1..n (6.28)
Итак, если известны
Sj0; j =
1..n,
То с помощью совокупности зависимостей (6.22) и (6.28), можно найти и
точечные статистические нормы
Mj0; j =
1..n
6.4. Определение вероятности фактического
познания истины
Для величины P,
как характеристики
всей системы
S, имеет место
P = max{p(s);
s = 1..m} (6.29)
Отсюда и из (6.23) имеем
h = max{h(s);
s = 1..m }
С учетом этого для нормального состояния системы S
из (6.23) и (6.26) получим
h = max{hj;
j = 1.. n } (6.30)
Оперируя совокупностью зависимостей (6.21),
(6.22), (6.26) и (6.30), всегда можно найти P.
А зная P,
можно найти и величины
Nj0; j =
1..n
Для этих величин, согласно (3.1), (4.5), (4.21)
и (4.29), имеет
место:
Nj0 = N0;
j = 1..n, (6.31)
где
N0 = 1 + round(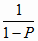 ,0)
(6,32) ,0)
(6,32)
6.5 Алгоритм определения точечных статистических
норм
1. По данным (6.4) вычисляют величины:
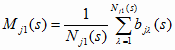 ; ;
и s = 1..m;
j = 1..n (6.33)
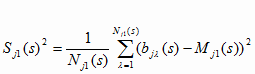
2. Последовательно устанавливают величины
Sj0 =
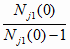 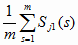 ;
j = 1..n ;
j = 1..n
hj(s) =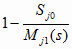 ;
j = 1..n; s = 1..m ;
j = 1..n; s = 1..m
hj = min{hj(s); s = 1..m); j = 1..n (6.34)
Mj0 = (1 -
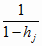 ) Sj0
; j = 1..n; ) Sj0
; j = 1..n;
h = max{hj; i = 1..n)
3. Составляют функцию
f(x) =
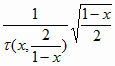 +
h -1 +
h -1
и находят корень P
уравнения
f(x) = 0; 0.5 ≤
x ≤ 0.99999,
где
t (x,
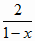 ) –
критическое значение критерия Стьюдента при
заданной доверительной вероятности x
и степени свободы m: ) –
критическое значение критерия Стьюдента при
заданной доверительной вероятности x
и степени свободы m:
m = round(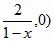
3. С помощью соотношения
Nj0 = N0
; j = 1..n
устанавливают величины
Nj0 ; j =
1..n,
где
N0 = 1 – round(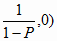
Итак, зная совокупность фактических данных (6.1)
и оперируя выше приведенным алгоритмом, можно установить величины
Mj0; Sj0
и Nj0;
j = 1..n,
служащие статистическими характеристиками нормального состояния ТП элементов
системы S.
Настоящий алгоритм впервые был опубликован в
[24] и [36].
6.6. Естественный глобальный оптимум и точечные
статистические нормы человека
Вообще
S = S(G) Þ P = max{p(s); s = 1..m}= P0,
где
S(G) –
генеральная совокупность объектов, описываемых с
помощью совокупности величин Y. А если S
Ì S(G),
то
P = max{p(s); s = 1..m}≤ P0
В том случае, когда
P = max{p(s); s = 1..m}= P0,
(6.35)
величины
Mj0; j =
1..n (6.36)
служат в качестве естественных глобальных оптимумов, а вся совокупность
величин (6.5)
служит характеристикой нормального состояния в общепринятом смысле.
Условие (6.35) будет выполняться, если среди
анатомических элементов системы S
можно найти такой s =
sN, для которого
будет иметь место
Mj1(s) = MjN, Sj1(s) = SjN
и Nj1(s) = NjN
при s = sN
для
всех j = 1..n
где
MjN, SjN
и NjN
- значения величин
Mj1(s), Sj1(s)
и Nj1(s)
для нормального состояния объекта s
В медицине совокупность величин
MjN, SjN
и NjN;
j = 1..n (6.37)
устанавливают по результатам обследования соответствующего контингента
здоровых людей.
Итак, для
того чтобы убедиться, что величины (6.36) служат в качестве естественных
глобальных оптимумов, в первую очередь,
нам необходимо проверять выполняется или нет
условие (6.35).
При этом полагают, что
P » P0
при .P ≥
P* и
P0 ≥ P*,
(6.38)
где
P* - требуемое
принимающим решения значение P.
В настоящее время, как правило, требуют, чтобы
P* ≥ 0.95 (6.39)
Это запись имеет смысл, если
P0 ≥ 0.95
А вообще должно иметь место
0.5 £ P**
£ P* < 1
Û 0.5 £ P**
£ P0 < 1
(6.40)
Отсюда и из (4.46)
имеем
P* = P**
≥ 0.95 при 7 £
n < ¥
Таким образом, в случаях,
когда n < 7,
требовать выполнение условия (6.39) не имеет
смысла. |