
Гл. 4. Закономерности гармонии природы
4.1. Закономерность существования целостной
системы - первый закон гармонии природы
В каждой целостной системе величины
Cj; j =1..n,
согласно (3.20), принимают только такие значения, которые находятся в
пределах области
[a , 1- a ].
Это говорит о том, что в каждой целостной системе
происходят только такие процессы, которые обеспечивают выполнение совокупности
условий (3.23), (3.27) и (3.28).
Иными словами, совокупностью зависимостей
(3.23), (3.27) и (3.28) описываются процессы, происходящие в целостных системах
и только в них, т.е. эта совокупность зависимостей является математическим
выражением закономерности существования целостных систем.
Итак, закономерность существования целостных
систем – первый закон гармонии природы:
«Любая материальная реальность
s в каждый момент времени
t = t0 (t1
≤ t0 ≤ t2)
с вероятностью p =
p(t0) (0.5 ≤
p(t0) ≤
p0 < 1) является целостной
системой, фактическое и возможное нормальное состояния которой в этот момент
времени соответственно определяются совокупностями данных
bjl 1;
l = 1..Nj1;
j =1..n
и
bjl 0;
l = 1..Nj0;
j =1..n,
взаимно связанными зависимостями
a + p = 1; 0
< a ≤ 0.5; 0.5 ≤
p < 1,
благодаря чему выполняется условие
0 < a ≤
Cj ≤ (1 - a )
для всех j =1..n,
представляющее собой математическое выражение целостности системы
s в момент времени
t = t0,
где
t 0 –
фиксированное значение t;
t1 – время
возникновения системы s: t1
≥ 0 ;
t2 – время
исчезновения системы s: t2
< ∞ ;
p – вероятность познания
истины в системе s в
момент времени t = t0;
p(t0) –
фиксированное значение P;
p0 –
максимально возможное значение p
для системы s
в момент времени t =
t0;
bjl 1
– результат измерения величины
yjÎ Y,
установленный l -им
«измерительным прибором» целостной системы s
в момент времени t0;
Y –генеральная
совокупность скалярных величин, служащих первичными показателями качества
функционирования системы s
в момент времени t =
t0;
Nj1 –
количество измерений величины
yjÎ Y,
произведенных в системе s
в момент времени t =
t0: Nj1
≥ 3;
n – объем
Y;
bjl 0
и Nj0
– значения bjl
1 и
Nj1 для возможного
нормального состояния системы s
в момент времени t =
t0: Nj1≤
Nj0 < ∞
;
a - вероятность
того, что система s в
момент времени t = t0
на изменение среды своего существования будет
реагировать неадекватно.
Cj -вероятность
того, что j –ой функциональный элемент системы s
в момент времени t =
t0 на изменение
среды своего существования будет реагировать адекватно».
Следует обратить внимание на то, что, согласно
первому закону гармонии, каждая материальная реальность s
является целостной системой с той вероятностью
p, с какою в этой
материальной реальности познается истину. А истина в каждой материальной
реальности, как было показано выше, познается с вероятностью
0.5 ≤ p < 1
Следовательно, любая МР является целостной системой с этой же вероятностью.
Иными словами, в природе не существует системы,
которая была бы целостной с вероятностью p = 1
или p < 0.5.
Принимая во внимание, что каждая материальная
реальность s является
целостной системой с той вероятностью p,
с какою в этой материальной реальности познается
истина, о величине p
можно говорить также, что она является вероятностью целостности системы
s при
t = t0.
4.2. Наиболее слабое звено целостной системы
Согласно общей теории систем каждая система
одновременно является и элементом системы
более высокого уровня. И наоборот, каждый элемент
системы одновременно является и системой элементов
более низкого уровня [5].
Отсюда следует, что каждый j –ой функциональный
элемент целостной системы s,
со своей стороны, тоже является целостной системой
элементов. Следовательно, для каждого j –го функционального элемента системы
s, аналогично (3.23),
(3.27) и (3.28), должно иметь место
Cj = 1- a
j; 0 <
a j ≤ 0.5; 0.5 ≤
Cj < 1, (4.1)
или, с учетом (3.34),
pj = 1 - a
j ; 0 <
a j ≤ 0.5; 0.5 ≤
pj < 1, (4.2)
Согласно (2.26) и (3.27) имеет место
C = 1- max{a
j; j = 1..n}
Отсюда и из (3.33) получаем
p = 1- max{a
j; j = 1..n}
и, в конечном счете, согласно (4.2),
p = pi , (4.3)
где
pi = min{pj;
j = 1..n} (4.4)
О функциональном элементе системы
s, для которого имеет место
(92), говорят, что он - наиболее слабое
звено системы s
в момент времени t =
t0.
В итоге, первый закон гармоний можно
сформулировать и так.
«Каждая материальная реальность
s является целостной
системой с вероятностью, равной вероятности целостности ее наиболее слабого
звена:
p = pi
при pi =
min{pj;
j = 1..n},
где
p -вероятность того, что
материальная реальность s
в момент времени t =
t0 является
целостной системой;
pj -вероятность
того, что j –ой функциональный элемент системы s
в момент времени t =
t0 является
целостной системой;
n –количество
функциональных элементов системы s
в момент времени t =
t0».
Это положение медициной признается издавна.
Ведь, хороший врач, обследуя больного, в первую очередь, всегда ищет самую
пораженную функциональную часть организма больного, т.е. ту часть, для которой
выполняется условие (4.2).
Почему врач так поступает? Потому что он знает,
что велика вероятность того, что эта функциональная
часть перестанет работать, если ей во -
время не помочь. И тогда перестанут работать и все остальные части организма
больного. Ведь, все эти части являются необходимыми составляющими одного целого
– организма больного! В итоге, человек погибнет.
Согласно (90) и (92)имеет место
a j =
a при
pi = min{pj;
j = 1..n},
т.е. величина a является характеристикой самого
слабого звена целостной системы s при t
= t0.
Следовательно, для того, чтобы была сохранена
целостность системы s, эта система, принимая
решение, должна ориентироваться именно на
величину a .
Отсюда смысл измерения величины yj
Î Y
в единицах Δj.
Итак, главная причина введения величин (2.37): с
их помощью система s принимает наиболее адекватное решение.
4.3. Закономерность внутрисистемной гармонии –
второй закон
гармонии природы
В главе 1 было показано, что процессы,
происходящие в МР, в конечном счете, описываются случайными величинами,
вероятности распределений которых подчиняются Закону Стьюдента.
Можно показать, что вообще благодаря Закону
Стьюдента, в ЦС, как МР, имеет место
зависимость:
Nj1 = m
для всех j = 1..n
(4.5)
где
m – натуральное число,
такое что имеют место
C = 1 -
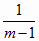 (4.6) (4.6)
и
3 £ m < ¥ (4.7)
В самом деле, по определению случайной величины
Tj,
описываемой распределением вероятностей Стьюдента, имеет место
Tj = 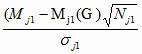 ;
j = j0; j0 = 1..n, ;
j = j0; j0 = 1..n,
где
Mj1(G) –
генеральное среднее арифметическое величины
yj Î Y
для ЦС s
при t =
t0;:
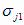 - «исправленное» среднеквадратичное
отклонение:
- «исправленное» среднеквадратичное
отклонение:
: 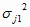 = =
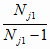 Sj12
Sj12
На практике, обычно полагают,
что [26, с. 212]:
Sj1(G) = 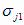 , ,
где
Sj1(G) – генеральное
среднеквадратическое отклонение величины yj
Î Y для ЦС
s при
t = t0.
Для простаты записи временно введем обозначение
nj = Nj1;
j = 1.. n (4.8)
Тогда можно написать, что
Tj =
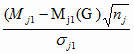 ; j
= j0; j0 =
1..n (4.9) ; j
= j0; j0 =
1..n (4.9)
Для плотности распределения вероятностей S(t,nj)
случайной величины Tj,
как известно, имеет место
S(t,nj) = B(nj) [1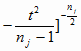 ,
(4.10) ,
(4.10)
где
B(nj) = 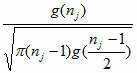 (4.11)
(4.11)
Здесь через g(x) обозначена гамма функция
от x.
Как видно, плотность распределения вероятностей
S(t,nj)
однозначно определяется
объемом выборки nj
и, следовательно, она не зависит от неизвестных
генеральных
параметров Mj1(G) и Sj1(G),
Пусть
tj = t(p,
(nj -1)) (4.12)
- значение Tj
такое, что
p º
Вер (½ Tj½
< tj) = 2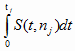 ,
(4.13) ,
(4.13)
где
p – вероятность того, что
ЦС s в момент времени
T на изменение среды
своего существования реагирует адекватно..
О величине tj
говорят, что она является критическим значением
Tj при
заданной доверительной вероятности p
и степени свободы (nj
– 1). Говорят также, что tj
является критическим значением критерия Стьюдента
при заданной доверительной вероятности p и
степени свободы (nj – 1).
Величина p
для ЦС s
в момент времени T,
как было показано в главе 3, является вполне
определенной. Следовательно, эта
величина никак не зависит от индекса j. Но тогда, согласно (4.10), (4.11),
(4.12) и (4.13), от индекса j не должны быть зависимыми и величины
nj; j = 1..n
т.е. должно иметь
место
n1 = n2 = = nn
Отсюда и из (4.8) имеем
N11 = N21 = = Nn1 (4.14)
Величины
Nj1; j = 1..n
по определению являются натуральными числами, для которых, согласно (1.19),
имеет место
3 £ Nj1 < ¥
; j = 1..n
Пусть, m* -
натуральное число, такое что
3 £ m* < ¥
(4.15)
Тогда зависимость (4.14) можно переписать в виде
Nj1 = m*
для всех j = 1..n
(4.16)
Покажем, теперь, что
m* = m
Для величин p,
согласно (3.32), имеет место
0.5 ≤ p < 1 (4.17)
Совокупность условий (4.15) и (4.17) будет
выполняться, если положим, что вообще
p= 1 - 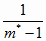 (4.18) (4.18)
Отсюда и из (3.33) имеем
C = 1 - 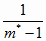 (4.19) (4.19)
Сопоставляя между собой зависимости (3.6) и
(3.19), заключаем, что
m* = m (4.20)
Отсюда и из (3.16) имеем
Nj1 = m для всех j = 1..n,
т.е. получаем (3.5).
Итак, благодаря распределению вероятностей
Стьюдента, в целостных системах всегда имеет место (3.5). При этом, согласно
(3.18) и (3.20), выполняется условие
p = 1 - 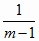 (4.21), (4.21),
указывающее на то, что величина p для каждой ЦС может принимать только
определенное дискретное значение. Им
является значение, установленное с помощью зависимости (4.21).
Пусть, mj–натуральное
число такое, что
mj =
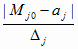 + 2 (4.22) + 2 (4.22)
Через mj,
как видно, обозначено количество значений величины
yj Î
Y, отдаленных друг от друга
на расстояние D j.
При этом все эти значения принадлежат области [ajmin,
ajmax].
Можно показать, что
mj = m для всех j =
1..n (4.23)
В самом деле, согласно (2.31) и
(3.1), имеет место
D j = a Mj0
(4.24)
А согласно (3.17), (3.19) и (4.22) имеем
mj = (1 - a )
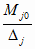 + 2 (4.25) + 2 (4.25)
Отсюда и из (2.11), (2.39) и (4.24) имеем
mj = 2 + 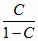
и, в конечном счете, согласно (3.27) и (4.6)
mj = m для всех j =
1..n
т.е. получаем (4.23).
Итак, измеряя величины
yjÎ Y; j = 1..n
в системных единицах
D j ; j = 1..n,
всегда будем обеспечивать выполнение условия (4.23).
Смысл зависимости (4.23): все первичные
показатели состояния целостной системы s
в каждый момент времени t
= t0 имеют
одно и то же количество друг от друга различаемых значений
Исходя из этого, закономерность, выраженная
зависимостью (4.23), в [28] нами была
названа закономерностью сохранения количества воспринимаемых значений.
Однако, последующее изучение вопроса показало, что
точнее назвать ее закономерностью
внутрисистемной гармонии.
Дело в том, что благодарю закономерности,
выраженной зависимостью (4.23),
внутренние ресурсы целостной системы
всегда распределяются рационально.
Они распределяются рационально в том смысле что, выполняется условие
p = pТ,
где
pT –тактическое
(ситуационное) оптимальное значение
p.
Величина pT
при заданных внутренних ресурсах целостной системы
служит тактическим (ситуационным) оптимальным значением p
в том смысле, что этими ресурсами в конце концов
будет достигнуто выполнение условия:
p = p0,
где
p0 –
максимально – возможное значение p
для ЦС s
в момент времени t = t0.
Причем, выполнение этого равенства может быть достигнуто в следующих четырех
случаях:
Случай 1.
Величина p
постепенно увеличивается, а величина
p0 остается
прежней.
В этом случае говорят, что целостная система
возвращается в свое прежнее нормальное
состояние. Так происходит, например, с момента
выздоровления человека, когда интервал времени выздоровления остается в пределах
интервала соответствующей возрастной группы.
Случай 2
Постепенно увеличиваются как величина
p, так и величина
p0.
Величина p0
постепенно может увеличиваться, например, в
результате систематических тренировок человека. Эта величина, как правило, также
увеличивается по мере увеличения порядкового номера
возрастной группы до достижения зрелости.
В этом случае говорят, что целостная система, в
конце концов, перешла в новое нормальное
состояние.
Случай 3.
Постепенно уменьшается
как величина p,так
и величина p0
и при этом имеет место:
p = p0 > 0.5.
Величина p0,
как правило, постепенно уменьшается по мере
увеличения порядкового номера старческой
возрастной группы.
В этом случае также говорят, что целостная
система переходит в новое нормальное
состояние.
Случай 4
Постепенно уменьшаются как величина
p, так и величина
p0, и это
уменьшение продолжатся до тех пор, пока не наступит время, когда
p = p0 = 0.5.
Так происходит, например, при постепенном
ухудшении состояния здоровья человека, когда, в конце концов, человек погибает.
В этом случае говорят, целостная система, в
конце концов, переходит в состояние, которое является и не является нормальным
одновременно, т.е. оно представляет собой неопределенное, граничное
состояние.
Следует отметить, что все выше рассмотренные
четыре случая имеют смысл для тех целостных систем, для нормального состояния
которых имеет место: p0 > 0.5.
Что касается целостных систем, для нормального
состояния которых имеет место: p0 =
0.5, то для них всегда выполняется условие:
p = p0 = 0.5.
В самом деле, по определению
p0, имеет место
0.5 ≤ p ≤ p0 < 1
(4.26)
Отсюда при p0 = 0.5
имеем: p =
p0 = 0.5.
Итак, закономерность внутрисистемной гармонии –
второй закон гармонии природы:
«В любой целостной системе
s в каждый момент времени
t = t0 (
t1 ≤ t0 ≤
t2 ) происходят
процессы, обеспечивающие выполнение условия
mj = m для всех j =
1..n,
где
t 0 –
фиксированное значение t;
t1 – время
возникновения системы s: t1
≥ 0 ;
t2 – время
исчезновения системы s: t2
< ∞ ;
mj – количество значений величины
yjÎ Y,
различаемых друг от друга в системе
s в момент времени
t = t0 ;
Y –генеральная
совокупность первичных показателей состояния системы s
в момент времени t =
t0 ;
m – фиксированное значение mj
:
m = 3, 4, 5, .., m0;
m0 – значение m
для возможного нормального состояния системы
s в момент времени
t = t0 ».
Согласно (3.27) и (4.25) имеет место
mj = C
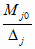 + 2;
j = 1..n + 2;
j = 1..n
Отсюда и из (4.23) имеем
m – 2 = C
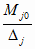 ; j
= 1..n (4.27) ; j
= 1..n (4.27)
Вместе с тем, согласно (4.6), имеет место
m – 2 = 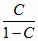
Отсюда и из (4.27) имеем
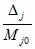 = (1 -
C) для всех
j = 1..n = (1 -
C) для всех
j = 1..n
и, в конечном счете, согласно (3.33),
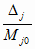 = (1 -
p) для всех
j = 1..n (4.28) = (1 -
p) для всех
j = 1..n (4.28)
Итак, в любой МР, как целостной системе,
происходят процессы такие, что при каждом
t = t0 (t1
£ t0
£ t2)
выполняется условие (4.28).
Каков смысл этого положения?
Вообще
s j0 =
s j0(t),
s j =
s j(t),
Δj =
Δj(t),
Mj0 = Mj0(t)
при t1
£ t £
t2
и (4.29)
p = p(t)
и p0 =
p0(t)
при t1
£ t £
t2
При этом
0.5 £ p(t) £ p0(t)
< 1 при t1
£ t £ t2 (4.30)
Пусть
p(s), t10
и t20
– значения
p0(t)
и t
такие, что имеют место
p0(t) £ p(s) < 1
при t1
£ t £ t2
и (4.31)
p0(t) = p(s) < 1 при
t1 < t10 £ t
£ t20 < t2
Об интервале времени от
t10 до
t20 говорят, что
он является периодом расцвета МР
s.
Для современного человека имеют место
t10 = 25 лет и
t20 = 45
лет.
Вообще, величины p
и p0
являются дискретными
функциями времени [19, 30]. При этом для величины
p0
выполняется условие
p0(t) →
p(s)
при t1 £
t £ t10
< t2
и
p0(t) → 0.5
при t20
£ t £
t2
А более точно, имеют место
p0(t) = p(s) = 0.5
при t < t1
p0(t) = p(ti1) при
t1£ ti1£
t £ ti+1,1< t10;
i = 1..n1 -1
и p0(t) = p(s) < 1
при t10
£ t £ t20
(4.32)
p0(t) = p(ti2) при
t20i2£ t£
t1+1,2£ t10; i = 1..n2
-1
p0(t) = p(s)
= 0.5 при t>t2,
где
n1 –
количество различаемых значений p0(t)
в интервале от t1
до t10;
n2 –
количество различаемых значений p0(t)
в интервале от t20
до t2.
В биологии и медицине издавна оперируют
словосочетанием «Поло - возрастная группа», полагая, что
Mi0(t) = Mj0(ti)
при ti£
t< ti+1; i = 1..n , (4.33)
где
n = n1 +
n2 +1
Вообще, как известно, переход от одного качества
в другое всегда происходит скачками,
т.е. условие (4.33) справедливо для любых материальных реальностей.
С учетом (4.33)
из (4.28)
получаем
Δji(t)
= Δj(ti)
при ti£
t< ti+1;
i = 1..n,
где
Δji(t)
= (1 - p(t)) Mj0(ti)
при ti£
t< ti+1;
j = 1..n (4.34)
Итак, смысл Закономерности внутрисистемной
гармонии:
В любой момент времени
t =t0 (ti
£ t0£
ti+1; i
= 1..n) МР
s может находиться в одном
из его возможных состояний от нормального до неопределенного. При этом, чем ее
состояние в момент времени t =t0
будет хуже, тем меньше будет величина
p = p(t0)
и, следовательно,
согласно (4.34),
тем большими будут величины
Δji(t0);
j = 1..n; i = i0; i0 = 1..n (4.35)
Самыми большими эти величины будут при p(t0)
= 0. 5, т.е. когда МР s
будет находиться в состоянии неопределенности.
Итак, величины (4.35) всецело зависят от
фактического состояния МР s.
В этом и состоит принципиальное различие
этих величин от величин
Δj(П)
и Δj*; j
= 1..n,
где
Δj(П)
– абсолютная ошибка измерительного прибора величины yj
Î Y,
используемого внешним наблюдателем
Δj*
- единица измерения величины
yj Î
Y, используемая внешним
наблюдателем: Δj*
≥ Δj(П).
Эти последние величины, как известно, никак не связаны с фактическим
состоянием МР s.
4.4. Мера внутри системной гармонии А.А.
Хускивадзе и здоровая среда
существования
ЦС
Пусть, для системы s
= 0 при t =
t0 имеет место
p = p0 =
P0 (4.36)
Равенство
p = p0
указывает на то, то система s является ТП анатомических элементов системы S,
а равенство
p = p0
говорит о том, что система s = 0
при t =
t0 находится в
нормальном состоянии и, следовательно, имеет место
Mj1 = Mj0
= Mj0(0); Sj1
= Sj0 = Sj0(0)
и Nj1
= Nj0 = Nj0(0)
для всех j = 1..n
(4.37)
Наконец, равенство
p = P0
свидетельствует о том, что условие (4.37) выполняется с вероятностью,
являющейся вероятностным пределом познания истины во всей большой системе
S при
t = t0.
Определение 4.1
Пусть, имеет место (4.36) и, следовательно,
выполняется условие (4.37).
Тогда и только тогда с вероятностью
p = P0
утверждают, в нормальном состоянии находится вся
система S.
С учетом (4.36) и (4.37) из (2.18), (2.19) и
(3.1) получаем
d j*
= . dj0(0) = Sj0(0)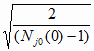 и t
j* = tj0(0)
= t (P0, 2 (Nj0(0)
– 1))
и t
j* = tj0(0)
= t (P0, 2 (Nj0(0)
– 1))
Отсюда и из (2.20), (3.1) и (4.5) имеем
d j(0) =
Sj0(0)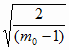 и t
j(0) = t (P0,
2 (m0 – 1))
и t
j(0) = t (P0,
2 (m0 – 1))
и, в конечном счете, согласно (3.1) и (2.21),
σj =
Sj0(0)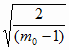 t (P0, 2 (m0
– 1)), (4.38)
t (P0, 2 (m0
– 1)), (4.38)
где
m0 – значение
m такое, что
m = m0
при p =
P0 (4.39)
С учетом (4.39) из (4.21), (4.36) и (4.48) получаем
σj =
Sj0(0)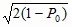 t (P0,
t (P0,
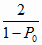 )), (4.40) )), (4.40)
Согласно (2.26), (2.27), (2.29) (3.1) и (4.37)
имеет место
a = max{a
j; j = 1..n}
и a 0
= min{a j;
j = 1..n} (4.41),
где
a j =
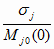 (4.42) (4.42)
Кроме этого, согласно (3.27) и (3.33), справедливо равенство
a + p = 1
С учетом этого из (4.36) и (4.41) получаем
a j =
a 0 = 1 – P0
для всех j = 1..n
(4.43)
Отсюда и из (4.40) и (4.42) имеем
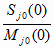
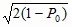 t (P0,
t (P0,
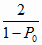 ) = 1 –
P0 для всех
j = 1..n (4.44) ) = 1 –
P0 для всех
j = 1..n (4.44)
Обозначим
h0 = 1 -
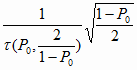 (4.45) (4.45)
Согласно (4.44) и (4.45) имеет место
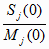 = 1 –
h0 для всех
j = 1..n, (4.46) = 1 –
h0 для всех
j = 1..n, (4.46)
Величина h0,
как видно из таблицы 4.1, является тем большей, чем
больше P0,
При этом, согласно (4.26) и (4.45), имеет место
0.325 £ h0 < 1
(4.47)
Таблица 4.1
Зависимость между величинами
P0 и
h0
| P0 |
0.500 |
0.600 |
0.700 |
0.800 |
0.900 |
0.950 |
0.990 |
0.999 |
0.9999 |
| h0 |
0.325 |
0.514 |
0.655 |
0.770 |
0.870 |
0.922 |
0.973 |
0.993 |
0.9980 |
Итак, зависимость (4.46) справедлива во всех
случаях, когда целостная система S
находится в нормальном состоянии.
Для того, чтобы живой организм находился в
нормальном состоянии, он, в первую очередь, должен быть здоровым.
Обратное утверждение, однако, не верно: если живой
организм является здоровым, то он может находиться в нормальном состоянии, а
может и не находиться. Все зависит от того, выполняется или нет им какая либо
работа.
Отсюда смысл следующего положения.
Определение 4.2
Пусть, для системы s при
t = t0
выполняется условие
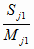 = 1 –
h для всех
j = 1..n, (4.48) = 1 –
h для всех
j = 1..n, (4.48)
где
h = 1 -
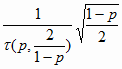 (4.49) (4.49)
и
0.325 £ h
£ h0 < 1
(4.50)
. Тогда и только тогда с вероятностью
p утверждают,
что внутренняя
среда существования
целостной системы s
в момент времени t =
t0 является
здоровой.
Определение 4.3
Пусть, внутренняя
среда существования
любой
целостной системы s = s0
(s0 = 0..m)
в момент времени t =
t0 является
здоровой.
Тогда и только тогда с вероятность P утверждают,
что внутренняя
среда существования
целостной системы S
в момент времени t =
t0 является
здоровой.
Определение 4.4
Пусть, внутренняя
среда существования
целостной системы S
в момент времени t =
t0 является
здоровой.
Пусть, при этом для любой целостной
системы s = s0 (s0
= 0..m) в момент времени
t = t0
имеет место
h = h0
и, следовательно, для любой целостной системы s
= s0 согласно
(4.45) и (4.49), имеет место (4.36) и (4.37).
Тогда и только тогда говорят, что система
S в момент времени
t = t0
находится в нормальном состоянии в широком
смысле.
О величине h0
говорят, что она является мерой внутренней
гармонией
системы S
в момент времени t = t0.
А величина h
является мерой внутри системной гармонии системы
s в момент времени t
= t0.
Зависимости (4.48) и (4.49) были установлены
А.А. Хускивадзе в 2003 году.
Впервые вопросы об особенностях здоровой
внутренней среды целостной системы были рассмотрены в [19] и [24].
4.5. Закономерность Всемирной гармонии – третий
закон гармонии природы
Пусть, при t = t0
система s
является идеальной парой и, следовательно, имеют
место
y1 + y2 =
0,
и (4.51)
yj = {yjmin,
yj0, yjmax};
j =1,2 ,
где
yj - первичный
показатель состояния j -ой
стороны пары s;
yjmin –
минимально - допустимое значение yj
для пары s
в момент времени t =
t0:
yjmin = D
j;
D j –системная
единица измерения величины yj:
yjо
– оптимальное (нормальное, среднее) значение
yj для пары
s в момент времени
t = t0:
yjо =
2 D j;
yjmax –
максимально допустимое значение yj
для пары s
в момент времени t =
t0:
yjmax = 3
D j .
Совокупность условий (4.51) будет выполняться,
если
y1 = y1min Û
y2 = y2min
y1 = y10
Û y2 =
y20 (4.52)
y1 = y1max
Û y2 =
y2max
Определение 4. 5
Пусть, пара s
такая, что в каждый момент времени t =
t0 (t1
£ t0
£ t2)
вероятность выполнения совокупности условий (4.51)
равна 0.5.
Тогда и только тогда говорят, что пара
s является простейшей
целостной системой и пишут:
p = p0 = 0.5 (4.53)
Ясно, что если совокупность условий (4.51)
выполнится при t = t0,
то состояние простейшей целостной системы
s будет нормальное, т.е.
будет иметь место одно из условий (4.52). В противном случае при t =
t0 не выполнится
ни одно из условий (4.52).
Таким образом, в простейшей целостной системе
реализуется логика «Все или ничего».
Поскольку целостная система, для которой имеет
место (4.53), является простейшей, любая другая целостная система будет
тем сложнее, чем величина p0
будет больше 0.5.
Под сложностью целостной системы здесь
понимается следующее.
Определение 4.6
Говорят, что система s(И)
является идеальной (предельно сложной)
целостной системой,
если выполняются следующие два условия.
1. Система s(И)
является целостной с вероятностью
p(И) = 1
и, следовательно, она всегда находится в нормальном состоянии,
где
p(И) – вероятность
фактического познания истины в системе s(И).
2. Каждая случайная величина
yj Î
Y(И) является
непрерывной, описываемой нормальным
распределением вероятностей fj(И)
с параметрами
0 < aj(И)
< ∞ и
s j(И)
= 0; j = j0;
j0 =1..n(И),
где
Y(И) –генеральная
совокупность первичных показателей состояния идеальной целостной системы
s(И);
aj(И)
–математическое ожидание непрерывной
случайной величины yjÎ
Y(И) для идеальной целостной системы
s(И) в момент времени
t = t0;
s j(И)
–генеральное среднеквадратическое отклонение величины yjÎ
Y(И) для идеальной целостной системы
s(И) в момент времени
t = t0;
n(И) – объем
Y(И).
О распределении вероятностей
fj(И)
говорят, что оно является идеальным (нереализуемым)
нормальным распределением вероятностей
случайной величины yjÎ
Y(И).
Примером идеальной целостной системы может
служить мироздание, если, конечно, оно является материальной реальностью, т.е.
имеет начало и конец существования.
Определение 4.7
Говорят, что система s
является реальной (реализуемой) целостной
системой, если
выполняются следующие условия
1. Система s
является целостной с вероятностью
0.5 £ p < 1
где
p – вероятность
фактического познания истины в системе s.
2. Каждая случайная величина
yj Î
Y описывается распределением
вероятностей fj
с параметрами
0 < aj
< ∞ и
s j > 0;
j = j0;
j0 =1..n,
где
Y – генеральная
совокупность первичных показателей состояния целостной системы
s;
aj –
математическое ожидание случайной величины yjÎ
Y(И) для целостной системы
s в момент времени
t = t0;
s j –
генеральное среднеквадратическое отклонение
величины yjÎ Y
для целостной системы s
в момент времени t =
t0;
n – объем
Y.
3. Имеют место
n = n(И)
и (4.54)
. aj® aj(И)
и s j
® s j(И)
= 0 при p0 ®
1 для всех j =1..n,
где
p0 –
вероятностный предел познания истины в системе s
в момент времени t =
t0.
4. Существует величина
0 £ r < 1 (4.55)
такая, что
p0 = 0.5 Û
r = 0 (4.56)
и
p0 ® 1
Û r ®
1 (4.57)
и, следовательно, имеет место
aj® aj(И)
и s j
® s j(И)
= 0 при r ® 1
для всех j =1..n
(4.58)
Тогда и только тогда говорят, что величина
r является мерой сложности
системы
s в момент времени
t = t0.
Ясно, что чем больше r
, тем сложней будет система
s.
Определение 4.7
Пусть
0.95 ≤ p0 < 1 (4.59)
Тогда и только тогда говорят, что система
s в момент времени
t = t0
является выраженной целостной системой.
О распределениях вероятностей
fj
j =1..n,
описывающих состояние выраженной целостной системы, говорят, что они являются
квазинормальными распределениями вероятностей.
Квазинормальное распределение вероятностей
fj,
в отличие от fj(И),
является вполне реализуемым.
Итак, Закономерность Всемирной гармонии – третий
закон гармонии природы:
«Наша действительность
представляет собой единство материальных реальностей, являющихся целостными
системами с вполне определенными максимально возможными вероятностями
целостности, принадлежащими к области
0.5 ≤ p0 < 1.
Величина p0
является наименьшей, т.е. равной 0.5 для
простейших целостных систем, представляющих собой идеальные пары
противоположных сторон.
Для любых других целостных систем значения
величины p0
являются тем большими, чем сложнее эти системы.
Наибольшие значения величина p0
принимает для биологических и других выраженных
целостных систем, описываемых многомерными квазинормальными распределениями
вероятностей».
В таком виде Закон Всемирной гармонии был
сформулирован А.А. Хускивадзе. К сожалению, не осталось документов, поясняющих,
почему ему понадобилось ввести
понятия квазинормального распределения вероятностей. Надо полагать, что он
имел в виду следующее.
При любом t = t0
в материальной реальности s
каждая величина y Î
Y, согласно (4.26) и
(4.28), имеет вполне определенное – конечное – количество друг от друга
различаемых возможных значений. Это означает, что для МР
s понятия «Непрерывная величина» не
существует. Следовательно, для МР s
не существуют и распределения вероятностей
непрерывных случайных величин. Это
относится, в частности, и к нормальному распределению вероятностей.

А.А. Хускивадзе
11.03.1975 – 30.01.2004
А.А. Хускивадзе
работал в
областях ядерной, атомной и молекулярной физики, в доказательной медицине и
обшей теории систем. В 2002 – 2003 годах его статьи публиковались в таких
ведущих журналах по физике, как “Journal
of Physics B:
Atomic, Molecular and Optical Physics”
и “Physics review”.
В 2004 году ему
посмертно присвоена степень доктора философии.
Разумеется, что если для МР
s нормального распределения
вероятностей не существует, это не означает, что нормального распределения
вероятностей не существует вообще. Оно существует, но не для МР
s. Это относится и к другим
распределениям вероятностей непрерывных случайных величин и, в частности,
распределению Стьюдента.
Понятие «Непрерывная случайная величина» - продукт абстрагирования
человеческого разума и оно применимо человеком, выступающим в роли внешнего
наблюдателя. Но оно не применимо для
«внутреннего наблюдателя состояния
организма» того же человека.
Выше сказанное справедливо для любой МР
s, в том числе и для
биологической системы.
Таким образом, утверждение, что биологические
системы описываются нормальным распределения
вероятностей, требует уточнения. Будет
правильнее сказать, что биологическая система описывается нормальным
распределением вероятностей с точки зрения
внешнего наблюдателя,
а с точки зрения «внутреннего наблюдателя
биологической системы» она описывается распределением вероятностей, близким к
нормальному
Ниже приводится чуть измененная редакция Закона
Всемирной гармонии. В ней нет упоминания о квазинормальном распределении
вероятностей, а делается акцент на следующее.
Для простейших целостных систем условие (4.56)
выполняется как при t1
£ t £
t2, так и при
t > t2.
Это означает, что простейшие целостные системы
всегда находятся в одном единственном – неопределенном –
состоянии.
Для материальных реальностей, состояние которых
меняется во времени, согласно (4.32), имеют место
0.5 £ p(t) £ p0(t)£
p(s) < 1 при t1
£ t £ t2 (4.60)
и
p(t) = p0(t) = p(s) = 0.5 при
t1 £ t £ t2
(4.61)
Зависимость (4.65) указывает на то, что
все материальные реальности, в конце концов, переходят в неопределенное
состояние, т.е. становятся простейшими целостными системами.
В итоге можно сказать, что простейшие целостные
системы являются «элементарными
кирпичиками» нашей действительности.
Итак, измененная редакция Закона Всемирной
гармонии:
«Наша действительность представляет собой
единство материальных реальностей, являющихся целостными системами с вполне
определенными максимально возможными вероятностями целостности, принадлежащими к
области
0.5 ≤ p0 < 1.
Величина p0
является наименьшей, т.е. равной 0.5 для
простейших целостных систем, представляющих собой идеальные пары
противоположных сторон.
Для любых других целостных систем значения
величины p0
являются тем большими, чем сложнее эти системы.
Наибольшие значения величина p0
принимает для биологических и других выраженных
целостных систем.
Все материальные реальности, являющиеся сложными
целостными системами, со временем переходят в неопределенное состояние и,
следовательно, становятся простейшими целостными системами.
Какая из двух вышеприведенных редакций
окажется жизнеспособной, покажет будущее.
Следует отметить, что Закономерность Всемирной
гармонии, уже доказала свое право на существование, А именно. она, совместно с
остальными двумя закономерностями гармонии, позволила нам получить
следующие очень важные результаты:
1.Создан способ определения естественного
глобального оптимума.
2. Разработан универсальный способ
количественного измерения качества функционирования материальных реальностей
живой и неживой природы.
А это приводит к тому, что медицина, биология и
социология отныне становятся точными науками,
какими являются физика и современная инженерия.
Способы, указанные выше, изложены в главах 5 и
6. А в приложении 1 представлена программа «Универсальный советчик принимающего
решения», реализующая эти способы на языке Mathcad 12.
В заключении отметим, что Закон Всемирной
гармонии А.А. Хускивадзе сформулировал в 2003 году. Закон существования
целостных систем и Закон внутрисистемной гармонии были сформулированы А.П.
Хускивадзе в 1983 году и впервые опубликованы1)
в [28]. Детальное обоснование этих закономерностей
приводится в [18],[19] и [29].
4.5. Критерий сложности систем М.А. Гайдеса и
вероятностный предел познания истины
Из Закона Всемирной гармонии следует, что между
величинами p0
и r существует тесная
взаимосвязь. Ее можно найти, основываясь на представлениях М,А, Гайдеса о
сложности систем [5].
Согласно М.А. Гайдесу система, выполняющая одну
определенную функцию и работающая по принципу «Все или ничего»,
является простой моно-функциональной системой.
А любая другая система s будет тем сложней, чем
больше количество составляющих ее простых монофункциональных систем, , т.е. чем
больше величина An2,
где
An2 –
количество размещений
n элементов по 2: An2
= n (n – 1).
Простая монофункциональная система Гайдеса, как
видно, представляет собой обычную простейшую целостную систему, состоящую из
n = 2 функциональных
элементов.
Следовательно, для нее должно иметь место
r = 0 при
n = 2 (4.62)
А для любой другой системы, как более
сложной, должно выполняться условие
r → 1 при
n → ¥ (4.63)
___________________________________________
1) Книгу [28] можно приобрести через
Интернет-магазин по адресу: URSS.ru
«Магазин научной книги. Раздел: Теория сложных
систем (больших систем)»
Совокупность условий (4.55), (4.56),
(4.57), (4.59), (4.62) и (4.63)
будет выполняться, если положим, что вообще
r = 1 -
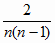 (4.64) (4.64)
и
p0 =
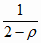 (4.65) (4.65)
В самом деле, согласно (2.2), имеет место
2 £ n <
¥
Отсюда и из (4.64) имеем
0 £ r < 1
r = 0 при
n = 2
r → 1 при
n → ¥
т.е. выполняются условия (4.55), (4.62) и (4.63).
Далее, согласно (4.65)
имеет место
p0 = 0.5 Û
r = 0
и
p0 ® 1
Û r ®
1,
т.е. выполняются условия (4.56) и (4.57).
Итак, все условия выполнены
В таблице (4.2) приведены значения величин
r и p0,
установленные для различных значений n.
Как видно, начиная с n
= 10, между величинами r
и p0 нет никакой разницы.
Они отличаются друг от друга лишь при маленьких
n, а точнее, когда
имеет место: n < 10.
Таблица 4.2
Зависимость между величинами n,
r и p0 <
| n |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
30 |
40 |
| r |
0 |
0.667 |
0.833 |
0.900 |
0.933 |
0.952 |
0.964 |
0.972 |
0.978 |
0.990 |
0.995 |
0.998 |
0.999 |
| p0 |
0.5 |
0.750 |
0.857 |
0.909 |
0.938 |
0.955 |
0.966 |
0.973 |
0.978 |
0.990 |
0.995 |
0.998 |
0.999 |
Как видно из таблицы (4.2) имеет место
0.95 ≤ r < 1 Û 0.95 ≤ p0
< 1
Отсюда и из (4.59) имеем
0.95 ≤ r < 1
Таким образом, можно говорить, что выраженная
целостная система всегда является сложной системой. И, наоборот, сложная система
всегда является выраженной целостной системой.
В заключение, из (4.64) и (4.65) находим
p0 = 1/(1 - 2/(n(n - 1))) (4.66)
|