Данная информация предназначена для специалистов в области здравоохранения и фармацевтики. Пациенты не должны использовать эту информацию в качестве медицинских советов или рекомендаций.
§3. Основные характеристики систем
Чтобы выполнять целенаправленные действия система должна иметь
соответствующие элементы. Это является следствием закона сохранения и
причинно-следственных ограничений, потому что ничего само собой не происходит.
Поэтому любые системы являются многокомпонентными объектами и их состав не
случаен. Именно состав систем во многом определяет их возможности выполнения
определённых действий. Например, система составленная из кирпичей может быть
домом, но не может быть компьютером. Но не только состав определяет возможности
систем. Необходимо ещё также и строго определённое взаимодействие между ними,
которое определяется их взаимоотношением. Двумя руками можно сделать то, что
невозможно сделать одной или одиночными руками, если можно так выразиться. Рука
обезьяны содержит те же пять пальцев, что и рука человека. Но рука человека
вместе с его мозгом преобразовала мир на Земле.
Таким образом, два существенных признака определяют качество и количество
результатов действия любых систем – состав элементов и их взаимоотношения.
Любой объект имеет только две основные характеристики: что и
сколько он может сделать. Рассмотрим обе характеристки результата действия
(что и сколько?) и попробуем выяснить, от чего зависят качество и количество
результата действия.
Качество результата действия.
Что может делать данный объект? Рассмотрим этот вопрос на примере группы
элементов, состоящей из трёх плоскостей (рис. 1А), свободно парящих в каком-либо
пространстве и посмотрим на их взаимодействие между собой и пробным шаром.
Предположим, что у каждой из плоскостей возможны три результата действия:
независимое движение в пространстве
толкание других предметов
соединение с другой плоскостью
А у шара есть только два возможных результата действия:
независимое движение в пространстве
толкание других предметов
Все три плоскости являются элементами группы и имеют совершенно одинаковые
свойства (качества результата действия). Шар не принадлежит данной группе и мы
его запускаем в игру только с одной целью – посмотреть, на что способна данная
группа и каждый её элемент в отдельности?
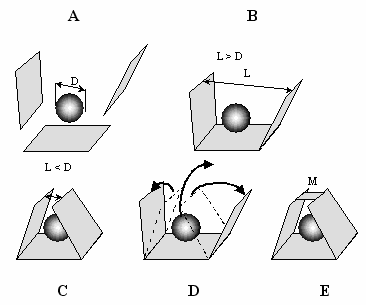
Рис. 1. Различные взаимодействия элементов.
И группа свободных элементов (А), и группа взаимодействующих элементов
(В), при условии L>D, имеют одинаковый результат действия - толкают шар, но не
лишают его свободы движения. При случайном уменьшении размера выхода полости по
отношению к диаметру шара (С) возникнет ловушка для шара, но при его движении
плоскости вновь могут разойтись и шар не лишается свободы движения (D). При
постоянной фиксации выхода полости (перемычка M, на рис. D) шар вообще лишается
свободы движения. При этом группа элементов из трёх плоскостей становится
ловушкой для шара, т.е., у этой группы появляется цель – лишить шар свободы
движения.
Шар и плоскости свободно двигаются в пространстве и толкают друг друга. При
этом неважно, сколько плоскостей имеется в данном пространстве, одна или три, их
количество не меняет их качества результатов действия. Все элементы сохраняют
свои свойства и шар сохраняет свою способность свободно двигаться в
пространстве. Все элементы группы взаимодействуют между собой. Суммарный
результат их совместного действия и результат действия каждой отдельной
плоскости всегда сохраняется один и тот же. В этом случае данная группа
элементов не является системой, а является набором случайных отдельных
элементов, поскольку как группа элементов, так и каждый из них в отдельности
обладают одинаковыми результатами действия.
Изменим условия эксперимента и заставим плоскости взаимодействовать таким
образом, чтобы их края, рёбра плоскостей, сцепились друг с другом (рис. 1В). В
результате такого взаимодействия одно из свойств плоскостей было нейтрализовано
(независимость движения), они стали двигаться в пространстве уже зависимо
друг от друга и появилось новое пространство (полость), ограниченное
плоскостями. Поместим внутрь его пробный шар и посмотрим, что с ним происходит?
Если размеры входа (выхода) новой полости больше диаметра шара (L > D, рис.
1В), то опять качественно ничего не изменилось, пробный шар по прежнему
сохраняет свои результаты действия (может свободно двигаться). Но если размер
выхода полости становится меньше диаметра шара (L < D, рис. 1С), то появляется
качественно новое свойство – система из трёх взаимодействующих элементов
превращается в ловушку для пробного шара, который лишается одного из своих
свойств – свободно двигаться в пространстве. Свойством ловушки не обладает ни
один отдельно взятый элемент группы. Таким свойством не обладают и
взаимодействующие элементы, при условии L > D. Только постоянное выполнение
условия L < D влечёт за собой появление нового качества – появления свойства
ловушки у группы из трёх элементов (плоскостей). Причём случайное и однократное
выполнение данного условия (L < D) не вызывает появление нового качества (рис.
1С), поскольку при движении шар раздвинет плоскости и уйдёт в пространство (рис.
3D). Только постоянное выполнение условия L < D превращает данную группу
из простого набора элементов в группу с качественно новым признаком (рис. 1Е).
Новое качество может быть только у группы определённым образом
взаимодействующих элементов. Определённый – значит целевой. Определённым образом
взаимодействующих – это значит имеющих определённую цель, построенных
определённым образом и действующих определённым образом для
достижения данной цели. Его не может быть у отдельно взятых элементов, и у
случайно взаимодействующих элементов. До выполнения этого условия группа
элементов была бесцельно парящей в пространстве случайной группой плоскостей.
После выполнения данного условия эта группа превратилась в новый элемент –
ловушку для шара.
В результате определённого взаимодействия элементов часть их свойств
нейтрализуется, а другая часть используется для достижения цели. Превращение
одних форм материи в другие происходит именно за счёт нейтрализации каких-то
свойств этих форм материи. А нейтрализация происходит за счёт изменения
каких-либо связей между элементами объекта, потому что эти связи определяют
форму объекта. Поэтому «нейтрализуется», но не «уничтожается», потому что ничто
в этом мире не исчезает и не появляется (закон сохранения). Весь мир состоит из
протонов, нейтронов и электронов, но мы видим различные объекты, которые
различаются по цвету, консистенции, вкусу, форме, молекулярному и атомарному
содержанию и т.д. Это значит, что при определённом взаимодействии протонов,
нейтронов и электронов появляются определённые межэлементарные связи. При этом
одни из их свойств нейтрализуются, а другие сохраняются или даже усиливаются
таким образом, что возникает всё многообразие нашего мира.
Целью любой системы является выполнение заданного (определённого) условия,
достижение заданного результата действия (цели). Если заданный результат
действия получился случайно, то в следующий момент он уже может не выполняться и
заданный результат исчезнет. Но если для для чего-то необходимо, чтобы результат
действия всегда (постоянно) был именно такой, а не какой-либо иной (задание
цели), необходимо, чтобы группа взаимодействую-щих элементов постоянно сохраняла
этот новый результат действия. Для этого данная группа элементов должна
постоянно стремиться сохранять заданное условие (выполнение цели). В
примере с плоскостями и пробным шаром этим условием является соблюдение
неравенства L < D, которое выполняется, например, перемычкой М (рис. 1Е), или
соединив расходящиеся края плоскостей.
Таким образом, группа элементов из трёх плоскостей может быть системой для
захвата пробного шара или любого другого тела подходящего размера, как может
быть и системой для нашей демонстрации, только в том случае, если она может
выполнить заданное условие (выполняет заданную цель). В данном случае, если
целью группы из трёх плоскостей является захват какого-либо тела и эта группа
может это сделать, она является системой.
Простая системная функциональная единица.
Система может состоять из любого количества исполнительных элементов, при
условии, что каждый из них может участвовать (содействовать) достижению цели и
их достаточно для реализации этой цели. Рассмотрим это на примере
системы-ловушки для червячка (рис. 2). Если какая-либо группа элементов состоит
из «m» элементов, причём только «n» из них взаимодействут, или в потенции могут
взаимодействовать для достижения цели (элементы «a»), то только эти «n»
элементов составляют систему. Остальные же элементы («b») не входят в состав
данной системы и их присутствие не влияет на достижение цели.
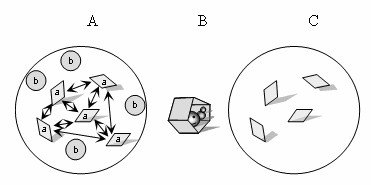
Рис. 2. Элементы системы-ловушки.
В некой группе есть два типа элементов – «a» (квадратные) и «b» (круглые
плоскости) (А). Цель системы – быть ловушкой для червячка (В). Цели системы
соответствуют только элементы типа «а», потому что только они могут сложится в
пятиугольную полость и быть ловушкой. Элементы типа «b» не содействуют заданной
цели и не являются элементами данной системы. Стрелками указаны взаимодействия
между элементами, которые приводят к достижению цели.
Если убрать эти элементы («b») из данной группы, то функции системы не
изменятся и не исчезнут (рис. 2С), потому что они не входят в в состав данной
системы.
Начнём убирать по одному элементы системы типа «a» из группы состава «n». По
мере убывания возможны два варианта следствий:
заданный результат действия системы уменьшится (изменение количественное)
заданный результат действия системы исчезнет (изменение качественное)
Будем убирать элементы из системы до тех пор, пока будет лишь уменьшение
количества результата действия, но чтобы качество системы сохранилось. Получим
систему (группу элементов) состава «k» с минимальным числом элементов, при
котором новое отличительное качество ещё сохраняется (рис. 3В). Если убрать ещё
хотя бы один элемент из состава «k», то у группы взаимодействующих элементов
качество ловушки исчезнет (рис. 3С).
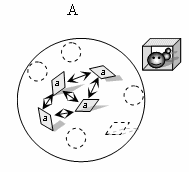
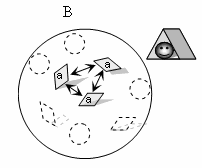
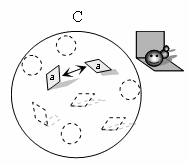
Рис. 3. Системная функциональная единица.
По мере удаления очередного элемента ловушка становится всё меньше и
меньше (A – четырёхугольная и B – треугольная полость), пока система перестаёт
быть ловушкой для червячка (C), поскольку в последнем случае червяк может
свободно удалиться от данной группы элементов. Группа элементов, представленная
на рис. B является системной
Отсюда, минимальной системой является такая группа из «k» элементов, которая
при удалении из её состава хотя бы одного любого элемента, теряет качество,
присущее данной группе элементов, но отсутствующее у любого из данных «k»
элементов.
В этом примере (рис. 3В) удаление любой плоскости лишает эту группу элементов
качества, которое отсутствует у каждого элемента группы в отдельности –
удерживать одного червячка. Цель этой группы – быть ловушкой для червячка.
Такая группа элементов является простой системной функциональной
единицей (простая СФЕ, не составная), минимальной простейшей системой, которая
имеет какой-либо признак (способность совершать действие), которого нет у любого
её элемента в отдельности.
Любая СФЕ реагирует на внешнее воздействие по закону «всё, или ничего». Этот
закон следует из определения простой СФЕ (удаление любого её элемента прекращает
её функцию как системы) и из дискретности её состава. Любой из её элементов
может либо быть, либо не быть в составе простой СФЕ. А поскольку простая СФЕ по
определению состоит из конечного и минимального набора исполнительных элементов
и все они должны быть в составе СФЕ и функционировать
(действовать), то прекращение функции любого из них прекращает функцию всей СФЕ
как системы. Независимо от силы внешнего воздействия, но при условии его
превышения определённого порога, её результат действия будет максимальным
(«всё»). Если нет внешнего воздействия, то СФЕ никак не проявляет себя (не
реагирует, «ничего»).
Простые СФЕ, несмотря на своё название, могут быть сколь угодно сложными – от
простейших минимальных СФЕ до максимально сложных. Молекула любого вещества
состоит из нескольких атомов. Удаление любого атома превращает эту молекулу из
одного вещества в другое. И даже каждый атом является очень сложным
образованием. Удаление любого его элемента превращает его в ион, другой атом или
другой изотоп.
Солдат является простой СФЕ системы под названием «армия». Солдат – это тело
человека плюс полное снаряжение солдата. Тело человека – чрезвычайно сложный
объект, но удаление любой его части делает из солдата инвалида. Да и солдатское
снаряжение также многокомпонентно. Но снаряжение не может стрелять без человека,
а человек не может стрелять без снаряжения. Только вместе они могут выполнять
функции, присущие СФЕ под названием «солдат».
Несмотря на внутреннюю сложность, которая может быть сколь угодно большой,
простая СФЕ является отдельным элементом, который выглядит как целое с
определённым единичным свойством (качеством) – совершать одно элементарное по
отношению ко всей системе определённое действие – захватывать шар, молекулу,
толкать порцию крови, развивать усилие в 0.003 грамма, обеспечивать условия
проживания животному (например, одна удельная единица площади леса) или человеку
(квартира), делать один выстрел и т.д. Любая СФЕ будучи разделена на части уже
перестаёт быть СФЕ для заданной цели. Только во взаимодействии частей группа
элементов может проявить себя как СФЕ. Когда ломается какая-нибудь вещь, хороший
хозяин всегда сначала раздумывает, где в хозяйстве ещё можно применить обломки и
лишь после этого выбрасывает их, потому что поломанную вещь (одна СФЕ) можно
превратить в другую, более простую (другая СФЕ).
Гемоглобин является элементом системы кровообращения и служит для захвата и
последующей отдачи кислорода. Следовательно, молекулы гемоглобина являются СФЕ
эритроцитов. Лиганды молекулы гемоглобина являются СФЕ гемоглобина, поскольку
каждая из них может служить ловушкой для молекул кислорода. Но дальнейшее
деление лиганды уже прекращает функцию удержания молекул кислорода.
Саркомер миокарда является элементом миокардиоцитов (клеток сердечной мышцы)
и служит для сокращения желудочков сердца. Однако для его нормальной работы
требуются элементы (органеллы) миокардиоцитов. Следовательно, миокардиоциты
являются СФЕ желудочков сердца, а саркомеры – СФЕ миоцитов. И т.д.
Аналогами СФЕ в неживом мире являются, например, все материальные частицы,
обладающие способностью при делении терять свои свойства – элементарные частицы
(?), атомы, молекулы и т.д.
Аналогом СФЕ в живом мире являются так называемые системные функциональные
единицы вентиляции (ФЕВ, в лёгких) и перфузии (ФЕП, тканевые и лёгочные
сосудистые модули, состоящие из групп капилляров, одновременно включающихся в
перфузию или отключающихся от неё) у различных животных. Но это примеры так
называемых составных СФЕ (см. ниже). Вирусы, возможно, могут быть системными
функциональными единицами наследственности (ФЕН). Так, вероятно, сначала
образовались полимерные молекулы типа ДНК в глинистых слоях или даже в
межпланетной пыли или на кометах, по типу автокаталитической реакции Бутлерова –
синтеза различных сахаров, в том числе и рибозы, из формальдегида в присутствии
ионов Ca и Mg, а рибоза является основой для создания РНК и ДНК, и только затем
уже появились клеточные структуры.
Эти примеры различных конкретных СФЕ показывают, что СФЕ не является чем то
неделимым, поскольку любая из них многокомпонентна и потому может быть разделена
на части. Только внутриатомные элементарные частицы претендуют на роль истинных
СФЕ, лежащих в основе всей материи нашего Мира, потому что пока не удаётся
разделить их на части. Потому они и называются элементарными. Возможно они также
очень сложно устроены, но не из элементов физического мира, а чего-либо другого,
и они являются результом действия систем не физического мира, вернее, не нашего
Мира форм. На это указывает существование парных виртуальных частиц, например,
позитрона и электрона, появляющихся как-бы из пустоты, из вакума и туда же
исчезающих. Мы не можем резать бумагу ножницами, сделанными из той же бумаги.
Вероятно, мы не можем также «разрезать» и элементарные частицы «ножницами»,
сделанными из этой же материи.
Простейший блок управления (прямая положительная связь).
Чтобы любая СФЕ могла действовать, она должна содержать определённые элементы
для осуществления своих действий согласно закону сохранения и
причинно-следственных ограничений. Для выполнения целевых действий система
должна содержать элементы исполнения, а для того, чтобы взаимодействие
элементов исполнения было целевым, система должна содержать элементы (блок)
управления.
Элементы исполнения (эффекторы) выполняют само определённое (целевое)
действие системы, чтобы получался заданный результат действия. Сам собой
результат действия не получится. Для его получения необходимо действие
определённых объектов. Такими элементами на примере плоскостей с пробным шаром
являются сами плоскости.
Но он (элемент исполнения) существует сам по себе и производит собственные
результаты действия в ответ на внешние по отношению к нему определённые
воздействия. Если на него что-то подействует, он прореагирует, не подействует –
не прореагирует. Взаимодействие с другими элементами его касается постольку,
поскольку результаты действия других элементов являются внешним воздействием для
него самого и могут вызвать его реакцию в ответ на эти воздействия. Эта реакция
проявится уже в виде его собственного результата действия, который также будет
внешним воздействием для других элементов системы, но не больше. Ни один
результат действия любого элемента системы не может быть результатом действия
самой системы по определению. Выполнилось ли заданное условие (цель системы)
случайно или не случайно, получился ли у данной группы элементов качественно
новый заданный результат действия, или что-то помешало этому, для любого
отдельно взятого элемента исполнения это совершенно безразлично. На
«самочувствии» элементов исполнения, т.е., на их собственных функциях это никак
не отражается и никакое их внутреннее свойство не заставит их следить за
выполнением генеральной цели системы. Они просто не «умеют» этого делать.
Элементы управления (блок управления) необходимы для того, чтобы
получался именно заданный, а не какой-либо иной результат действия. Так как
целью является реакция в ответ на специфическое внешнее воздействие, то
сначала нужно почувствовать его, выделить его из множества других
неспецифических внешних воздействий, принять решение о каких-либо
специфических действиях и начать действовать.
Если, например, СФЕ реагирует на давление, то она должна уметь «чувствовать»
(рецепция) именно давление, а не температуру или что-либо другое. Для этого у
неё должен быть специальный орган (рецептор), который умеет это делать. А для
того, чтобы реагировать только на специфическое внешнее воздействие,
которое может иметь отношение к выполнению её цели, СФЕ должна не только иметь
рецепцию, но и выделить его из всех остальных внешних воздействий,
которые действуют на неё (селекция). Для этого у неё должен быть специальный
орган (селектор, или анализатор), который умеет выделять нужный сигнал из массы
других. Далее, почувствовав и выделив внешнее воздействие она должна принять
решение о том, что нужно действовать (принятие решения). Для этого у неё
должен быть специальный орган для принятия решений, который может принимать
решения. Затем она должна реализовать это решение, т.е., заставить
элементы исполнения действовать (реализация решения). Для этого у неё должны
быть элементы (стимуляторы), с помощью которых можно передать решение на
элементы исполнения.
Следовательно, чтобы прореагировать на определённое внешнее воздействие и
получить необходимый результат действия необходимо выполнить выполнить следующую
цепочку управляющих действий :
рецепция → селекция → принятие решения → реализация решения (стимуляция)
Какие элементы должны выполнять эту цепочку действий управления?
Элементы исполнения (например, плоскости) этого делать не могут, потому что
выполняют само действие, например, захвата, но не действия управления.
Поэтому они и называются элементами исполнения.
Все действия управления должны выполнять элементы управления (блок
управления) и они должны входить в состав СФЕ.
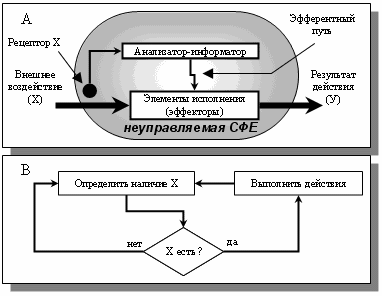
Рис. 4. Неуправляемая простая СФЕ (А) и алгоритм работы её блока
управления (В).
Блок управления состоит из (рис. 4):
рецептора Х (выделяет специфичный сигнал и определяет наличие внешнего
воздействия)
афферентных путей (передают информацию с рецептора в анализатор)
анализатора-информатора (на основе информации с рецептора «Х» вырабатывает
решения об активации исполнительных элементов)
эфферентных путей (стимулятора) (реализация решения, передают управляющие
воздействия на эффекторы)
Рецептор «Х», афферентные пути, анализатор-информатор (побудитель к
действию) и эфферентные пути (стимулятор) вместе составляют блок управления.
Рецептор и афферентные пути является прямой положительной связью (ППС). Прямой
потому, что внутри СФЕ сигнал управления (информации о наличии внешнего
воздействия) идёт в том же направлении, что и само внешнее воздействие.
Положительной потому, что если есть сигнал, есть реакция, нет сигнала, нет
реакции.
Таким образом, блок управления СФЕ реагирует на внешнее воздействие. Он может
почувствовать и выделить специфический сигнал внешнего воздействия из множества
других внешних воздействий и, в зависимости от наличия или отсутствия
специфичного сигнала решить, делать собственное действие или нет. А его
собственным действием является побуждение (стимуляция) элементов исполнения
действовать.
Есть неуправляемые (рис. 4) и управляемые СФЕ (рис. 5). Блок управления
неуправляемых СФЕ решает действовать или нет только в зависимости от наличия
внешнего воздействия. Блок управления управляемых СФЕ также решает действовать
или нет в зависимости от наличия внешнего сигнала, но при наличии
дополнительного условия – разрешения на это действие, которое подаётся на его
вход уставки.
У неуправляемой СФЕ есть один вход для внешнего воздействия и один выход для
результата действия. Логика работы такой СФЕ чрезвычайно простая – если есть
определённое внешнее воздействие, то она действует (есть результат действия),
если нет внешнего воздействия, то нет результата действия. Для неуправляемых СФЕ
регулятором действия является само внешнее воздействие. У неё есть собственное
управление, осуществляемое внутренним блоком управления. Но у такой СФЕ
невозможно внешнее управление. Она сама решает, действовать ей, или нет. Поэтому
она называется неуправляемой. Это решение зависит только от наличия внешнего
воздействия. Если есть внешнее воздействие, то она действует и никакое внешнее
решение (не воздействие) не может изменить внутреннего решения данной СФЕ.
Неуправляемая СФЕ независима от внешних решений. Если она «решила», то выполнит
свое действие.
Примером неуправляемой СФЕ является, например, молекула нитроглицерина (СФЕ
для микровзрыва). Если её тряхнуть (внешним воздействие является тряска), то она
начнёт распадаться, выделяя энергию, и во время этого процесса ничто не
остановит её от распада.
Аналогом неуправляемых СФЕ в живом организме являются саркомеры, лиганды
гемоглобина и т.д. Если саркомер начал сокращаться, он не остановится, пока не
закончит сокращение. Если лиганда гемоглобина начала захватывать кислород, она
не остановится, пока не закончит захват.
В отличие от неуправляемых у управляемых СФЕ есть два входа (один для входа
внешнего воздействия и один – для ввода уставки в анализатор) и один выход для
результата действия (рис. 5). Логика работы управляемой СФЕ несколько отличается
от логики работы неуправляемой СФЕ. Такая СФЕ будет давать результат действия не
только в зависимости от наличия внешнего воздействия, но и от наличия
разрешения на входе уставки.
Если есть определённое внешнее воздействие и есть разрешение на входе уставки,
то действие начнёт выполняться. Если есть внешнее воздействие и нет разрешения
на входе уставки, тот не должно быть действия. Для управляемых СФЕ регулятором
действия является разрешение на входе уставки. Потому такие СФЕ называются
управляемыми.
Аналогом управляемой СФЕ в живом организме являются, например, лёгочные
функциональнальные единицы вентиляции (ФЕВ) или перфузии (ФЕП-МКК), тканевые
функциональнальные единицы перфузии (ФЕП-БКК), функциональные единицы секреции
(клетки желёз различной секреции, ФЕС), нефроны почек, ацинусы печени и т.д.
Элементы блока управления построены (собраны) из других обычных элементов,
подходящих по своим характеристикам. Он может быть построен как из самих
исполнительных элементов, соединённых определённым образом и по совместительству
выполняющих функции исполнения и управления, так и из других не принадлежащих к
данной группе исполнительных элементов и выделеных в отдельную цепь управления.
В последнем случае они могут быть точно такими же, как и исполнительные
элементы, но также могут быть сделаны и из других элементов. Например, мышечные
сократительные функциональные единицы состоят из мышечных клеток, но управляются
нервными центрами, состояшими из нервных клеток. В тоже время все виды клеток,
как нервных, так и мышечных, построены почти из одинаковых строительных
материалов – белков, жиров, углеводов и минералов.
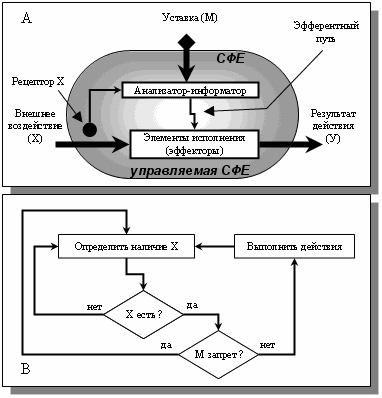
Рис. 5. Управляемая СФЕ (А) и алгоритм работы блока её управления (В).
Отличие управляемой СФЕ от неуправляемой только в наличии входа уставки.
Отсюда же и изменение алгоритма её работы. Действия управляемой СФЕ зависят не
только от внешнего воздействия, но и от запрета М на входе уставки.
Блок управления является простейшим если он содержит только ППС
(рецептор «Х» и афферентные пути), анализатор-информатор и стимулятор.
СФЕ являются первичными ячейками, исполнительными элементами любых систем.
Как видим, несмотря на свою примитивность, они представляют собой довольно
сложный и многокомпонентный объект. Каждая из них содержит не менее двух типов
элементов (управления и исполнения), и каждый тип включает в себя ещё и ещё, но
эти элементы являются обязательными атрибутами любой СФЕ.
Сложность СФЕ является сложностью иерархии их элементов. Особой разницы между
элементами исполнения и элементами управления нет. В конечном итоге всё в этом
мире состоит из электронов, протонов и нейтронов. Разница между ними только в их
месте в иерархии систем, т.е., в их взаимном расположении.
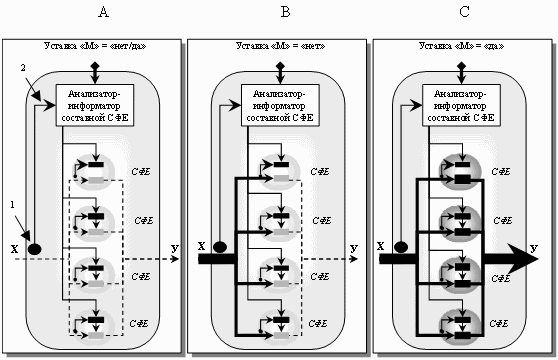
Рис. 6. Составная СФЕ в режиме ожидания (А), запрете функции (В) и её
реализации (С).
Составная СФЕ содержит 4 простых СФЕ. Если нет никакого внешнего
воздействия, все простые СФЕ неактивны, нет никакого результата действия (А).
Если есть внешнее воздействие «Х», но уставка вносит «нет» (запрет на действие),
все СФЕ также неактивны и также нет результата действия (В). Если есть внешнее
воздействие и уставка вносит «да» (разрешение на действие), то все СФЕ активны и
есть результат действия (С). «Мощность» данной составной СФЕ в 4 раза больше
«мощности» простой СФЕ. Активация СФЕ производится через вводы уставки их блоков
управления. У каждой простой СФЕ есть собственная ППС и общая для них всех ППС.
1 – рецептор «X»; 2 – прямая положительная связь.
Из неуправляемых и управляемых СФЕ можно строить другие СФЕ (составные, рис.
6), более мощные, чем одиночная СФЕ. В реальном мире мало простых СФЕ, которые
дают минимальный неделимый результат действия. Гораздо больше составных СФЕ.
Например, патрон, наполненный крупинками пороха является составной СФЕ (СФЕ для
выстрела), но его энергия взрыва намного больше энергии одиночной крупинки
пороха.
Блок-схема составной СФЕ очень похожа на блок-схему простой СФЕ.
Отличие составной СФЕ от простой только количественное. Простая СФЕ содержит
только одну СФЕ – саму себя, а составная содержит несколько СФЕ, потому есть
возможность усиления результата действия.
Таким образом, простая и составная СФЕ содержат два типа элементов:
- элементы исполнения (эффекторы, которые выполняют специфические
действия для достижения заданной генеральной цели системы)
- элементы (блок) управления (ППС, анализатор-информатор и стимулятор,
который активирует СФЕ)
У составной СФЕ такой же блок управления, как и отдельной СФЕ, т.е.,
простейший, с прямой управляющей связью (ППС). Составные СФЕ также работают по
принципу «всё или ничего». Т.е., они либо дают максимальный результат действия в
ответ на внешнее воздействие, либо ждут это внешнее воздействие и не делают
никаких действий. Отличие составных СФЕ от простых СФЕ только в силе или
амплитуде реакции, которая пропорциональна числу простых СФЕ.
Если костяшки домино стоят в последовательном ряду, то их результатом
действия будет долгий звук от падения костяшек, длительность которого равна
сумме числа падений каждой костяшки (увеличение длительности результата
действия). Если костяшки стоят в параллельном ряду, то их результатом действия
будет короткий, но громкий звук, равный сумме громкостей от падения каждой
костяшки в отдельности (увеличение мощности).
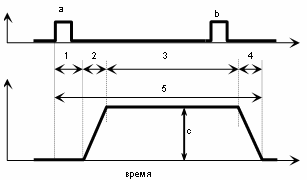
Рис. 7. Полный цикл и микроциклы функции простой идеальной составной СФЕ.
a – внешнее воздействие на которое СФЕ начинает реагировать; b – внешнее
воздействие, на которое СФЕ не реагирует, потому что находится в рефрактерном
состоянии (не может активировать исполнительные элементы, потому что они уже
активированы); с – амплитуда результата действия СФЕ на графике функции СФЕ.
1 – восприятие и селекция внешнего воздействия рецептором “X” после начала
внешнего воздействия и принятие решения; 2 – активация элементов исполнения; 3 –
выполнение действия элементов исполнения; 4 – прекращение функции; 5 – полный
цикл функции СФЕ.
Цикл работы идеальной простой и составной СФЕ складывается из микроциклов
(рис. 7):
восприятие и селекция внешнего воздействия рецептором «X» и принятие
решения
воздействие на исполнительные элементы (СФЕ)
срабатывание исполнительных элементов (СФЕ)
прекращение функции.
После начала внешнего воздействия срабатывает рецептор «X» (1-й микроцикл).
Затем уходит какое-то время на принятие решения, потому что это решение само
является результатом действия определённых СФЕ, входящих в состав блока
управления (2-й микроцикл). Затем активируются (включаются) все СФЕ (3-й
микроцикл). Время срабатывания СФЕ зависит от скорости утилизации энергии,
затраченной на действие СФЕ, например, от скорости сокращения саркомера в
мышечной клетке и которое определяется скоростью биохимических реакций в
мышечной клетке. После этого все СФЕ прекращают свою функцию (4-й микроцикл).
При этом СФЕ полностью затрачивает на своё действие всю ту энергию, которую она
имела и могла использовать на это действие. А так как очередность действий и
результат действия всегда один и тот же, то и эта мера энергии всегда одна и та
же (квант энергии). Чтобы СФЕ снова могла совершить новое действие, её нужно
снова «зарядить» энергией. На это также может уходить время (время зарядки
энергией, на графике не показано). Как это происходит рассмотрено в разделе,
посвященном пассивным и активным системам, см. ниже).
У любой СФЕ цикл её деятельности складывается из этих микроциклов. Поэтому,
её время цикла (5 на рис. 7) работы всегда одинаковое и равно сумме этих
микроциклов. Если СФЕ начала свои действия, она не остановится, пока не завершит
свой полный цикл. В этом причина неуправляемости любых СФЕ в процессе их
срабатывания (абсолютная рефрактерность) – внешнее воздействие может быстро
закончиться и снова начаться (b на рис. 7), но пока СФЕ не закончит свои
действия, она не остановится и не будет реагировать на новое внешнее
воздействие.
В реальных составных СФЕ к этим микроциклам могут добавляться дополнительные
микроциклы, обусловленные несовершенством реальных объектов, например,
несинхронностью срабатывания элементов исполнения из-за их неодинаковости.
Отсюда видно, что даже простейшие системы, каковыми являются СФЕ, срабатывают
не сразу, а им требуется какое-то время, пока появится их результат действия.
Этим объясняется иннерционность систем, которую можно измерить, используя
параметр постоянной времени. Но это, вообще говоря, не иннерционность, а
транзиторная (проходящая) инертность объекта (рефрактерность), его
неспособность отвечать на внешнее воздействие в определённые фазы своего
действия. Истинная иннерционность объясняется независимостью результата действия
от системы его произведшей (см. ниже).
Постоянная времени – это время между началом внешнего воздействия и
готовностью к новому внешнему воздействию после выработки результата действия.
Аналогом составных СФЕ являются все объекты, которые действуют подобно
лавине. В таких случаях работает «принцип домино». Было одно воздействие и всё
падает. Но число падений равно числу СФЕ. Если толкнуть одну костяшку домино, от
падения будет только один щелчок. Если толкнуть ряд стоящих костяшек домино,
будет столько щелчков, сколько костяшек домино стояло в ряду.
Биологическим аналогом составных СФЕ являются, например, функциональные
единицы вентиляции (ФЕВ), каждая из которых состоит из большой группы в
нескольких сот альвеол, одновременно включающихся в процесс вентиляции или
отключающихся от неё. Ацинусы в печени, сосудистые сегменты брыжжейки, лёгочные
сосудистые функциональные единицы и пр. являются аналогами составных СФЕ.
Таким образом, простая СФЕ является объектом, который может
реагировать на определённое внешнее воздействие, а результат её действия всегда
максимальный, потому что блок управления не контролирует его, т.е., она работает
по закону «всё или ничего». Тип её реакции обусловлен типом СФЕ. Есть два вида
простой СФЕ – неуправляемая и управляемая. Обе они срабатывают от
специфического внешнего воздействия. Но для срабатывания управляемой СФЕ
дополнительно необходим ещё сигнал внешнего разрешения на входе уставки, а у
неуправляемой СФЕ входа уставки нет. Поэтому неуправляемая СФЕ не зависит ни от
каких внешних управляющих сигналов. Блок управления управляемой и неуправляемой
СФЕ состоит из анализатора-информатора и имеет только ППС (информатор «Х» и
афферентные пути).
Составная СФЕ является таким же объектом, как и простая СФЕ, но результат
её действия усиленный. Она также работает по закону «всё или ничего» и её
реакция обусловлена типом и числом её СФЕ. Вероятно, и составные СФЕ могут быть
управляемыми и неуправляемыми, и различие между ними только в наличии входа
уставки в общий блок управления, через который в него подаётся разрешение на
выполнение действия. Блок управления системы тоже простейший, имеет только ППС и
анализатор-информатор.
Следовательно, любые СФЕ функционируют по закону «всё или ничего». СФЕ так
устроена, что она либо ничего не делает, либо выдаёт максимум результата
действия. Её элементарный результат действия – либо он есть, либо его нет. Может
быть СФЕ, которая выдаёт результат действия, например, в два раза больший, чем
результат действия другой СФЕ. Но он всегда будет в два раза больший.
Каждый результат действия простой СФЕ является квантом действия (неделимой
порцией), причём максимальным для данной СФЕ. Неделимым потому, что СФЕ не может
выдать часть своего результата действия, например, половину. А раз «неделимой
порцией», то не может быть градации. СФЕ может быть, например, открыта или
закрыта, давать электрический ток, или не давать, секретировать что-либо или не
секретировать, и т.д. Но она не может регулировать количество результата
действия поскольку её результат всегда либо отсутствует, либо максимальный.
Такой режим работы очень грубый, не точный и не выгодный как для самой СФЕ,
так и для её цели. Представим себе, что в нашем автомобиле вместо руля будет
устройство, которое будет сразу максимально сворачивать вправо, если мы повернём
руль направо, или максимально влево, если мы повернём налево. Вместо плавной и
точной подстройки под заданный курс движения автомобиль будет резко метаться
справа налево. И цель не будет достигнута, и автомобиль будет разрушен.
В принципе составная СФЕ могла бы дать градуированный результат
действия, потому что у неё есть несколько СФЕ, которые она могла бы включать в
разной последовательности. Но такая система не может сделать этого, потому что
не «видит» свой результат действия и не может его сравнить с тем, что должно
быть.
Количество результата действия.
Для достижения заданной цели только задания качества результата действия
недостаточно. Цель задаёт не только «какое действие должен» сделать объект (качество
результата действия), но и «сколько этого действия» должен сделать данный
объект (количество результата действия). А система должна стремиться
выполнить специфическое действие ровно столько, сколько нужно, ни больше и ни
меньше. Качество действия определяется типом СФЕ. Количество определяется
количеством СФЕ.
Есть три количественные характеристики результата действия – максимум,
минимум и оптимум количества действия. В реальном мире от реальных
систем требуется градация их результатов действия. Поэтому в работе системы
должен быть не максимум и не минимум, а оптимум.
Оптимум, это функционирование по принципу –необходимо и
достаточно. Результат действия необходимо должен быть таким, а не другим по
качеству, и достаточным по количеству, ни больше и не меньше. Отсюда, СФЕ не
могут быть полноценными системами. Необходимы системы, у которых возможна
регулируемая градация результата действия.
Например, требуется, чтобы в тканевых капиллярах было давление 10 мм Hg. Этой
фразой сразу задаётся всё, что содержится в понятии «необходимо и достаточно».
Необходимо... давление, и достаточно... 10 мм Hg. Можно подобрать
СФЕ, которая даёт давление, но не 10 мм Hg., а, например, 100 мм Hg. Это слишком
много. Вероятно, можно подобрать СФЕ, которая может давать давление 10 мм Hg и в
данный момент этого достаточно. Но если ситуация вдруг изменилась и уже
требуется 100 мм Hg, а не 10 мм Hg, тогда что делать? Снова «бегать» и искать
СФЕ, которая может давать 100 мм Hg? А нельзя ли сделать такую систему, которая
могла бы давать любые давления в диапазоне, например, от 0 до 100 мм Hg, в
зависимости от ситуации?
Чтобы давать то количество результата действия, которое необходимо в данный
момент, необходима градация результатов действия систем. Это можно было бы
достичь путём построения систем из набора однотипных СФЕ по типу блок-схемы
составной СФЕ (рис. 6). У неё есть то, что необходимо для градуировки результата
действия – она содержит много СФЕ. Если сделать так, чтобы можно было включать в
действие от одной до всех СФЕ, в зависимости от потребности, то результат
действия будет иметь столько градаций, сколько СФЕ есть в системе. Чем больше
точности требуется, тем больше мелких градаций результата действия должно быть.
Поэтому, вместо одной СФЕ с её предельно большим результатом действия нужно
использовать столько СФЕ с маленькими результатами действия, сумма которых равна
требуемому максимуму, а точность выполнения цели равна результату действия одной
СФЕ.
Но у составной СФЕ нет возможности регулировать свой результат действия,
потому что у неё нет органа, который делал бы это. Для того, чтобы выдать
результат действия в точности равный заданному, его (результат действия) нужно
постоянно измерять и сравнивать данные измерений с заданием (с уставкой, с
«базой данных»).
«База данных» – это список тех должных величин результата
действия, которые система должна выдать в зависимости от величины внешнего
воздействия и алгоритма работы блока управления. Цель системы – каждому значению
измеренного внешнего воздействия должна соответствовать строго
определённая величина результата действия (должная величина).
Для этого нужно «видеть» (измерять) результат действия системы, чтобы
сравнивать его с должным. А для этого у блока управления должен быть рецептор
«У», который может измерять результат действия, должна быть линия связи
(реципрокные пути), по которым информация с рецептора «У» идёт в
анализатор-информатор, где результат этого измерения должен сравниваться с тем,
что должно быть (с «базой данных»). Блок управления системы должен сравнивать
внешнее воздействие с должной величиной, а должную величину с собственным
результатом действия, чтобы увидеть его соответствие или несоответствие должной
величине. Сравнить внешнее воздействие с должной величиной составная СФЕ ещё
может, потому что у неё есть ППС. А сравнить должную величину с результатом
собственного действия составная СФЕ уже не может, потому что у неё нет ничего
(нет соответствующих элементов), что может это сделать.
Простой блок управления (отрицательная обратная связь).
Чтобы блок управления системы мог «увидеть» (почувствовать и измерить)
результат действия системы, он должен иметь соответствующий рецептор «У» на
выходе системы и линию связи между ним и рецептором «У» (реципрокный путь).
Логика работы такого управления заключается в том, что если результат
действия больше заданного, то нужно его уменьшить, активировав меньшее число СФЕ,
если меньше – то увеличить, активировав больше число СФЕ. Поэтому такая связь
называется отрицательной. А так как информация движется обратно, от
выхода системы в сторону её начала, она называется обратной. В
итоге получается отрицательная обратная связь (ООС).
Рецептор «У» и реципрокный путь составляют ООС, а вместе с
анализатором-информатором и эфферентными путями (стимулятором) составляют
петлю ООС. В зависимости от потребности и на основе информации ОСС блок
управления по мере необходимости включает или выключает функции управляемых СФЕ
(рис. 8).
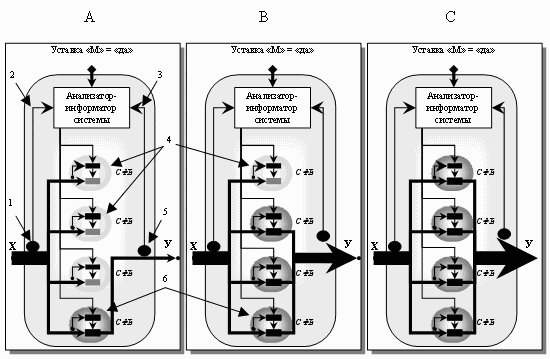
Рис. 8. Блок-схема системы с простым блоком управления. Отрицательная
обратная связь.
Отличие данной системы от составной СФЕ только в наличии рецептора «У»,
который измеряет результат действия, и реципрокных путей, по которым информация
передаётся с этого рецептора в анализатор. А – активна одна СФЕ, В – активны три
СФЕ, С – активны все СФЕ. Число активных СФЕ определяется ОСС.
1 – рецептор "Х"; 2 – ППС.; 3 – ООС; 4 – неактивные СФЕ; 5 - рецептор «У»
для измерения результата действия системы; 6 – активные СФЕ.
Следовательно, ООС реализуется с помощью петли ООС, которая включает в себя
рецептор «У», реципрокный путь, по которым информация с рецептора «У»
переносится в анализатор-информатор, сам анализатор и эфферентные пути, через
которые решения блока управления передаются на эффекторы (управляемые СФЕ).
Таким образом, система, в отличие от СФЕ, содержит как ППС, так и ООС. Прямая
управляющая связь активирует систему, а отрицательная обратная связь определяет
число активированных СФЕ.
Например, если в лёгких будет будет открыто больше альвеолярных капилляров,
чем есть альвеол с подходящим газовым составом, то артериализация венозной крови
будет неполной, и нужно закрыть ту часть альвеолярных капилляров, которые
«омывают» кровотоком альвеолы с неподходящим для газообмена газовым составом.
Если их будет открыто меньше, будет перегрузка лёгочного кровообращения и
давление в лёгочной артерии возрастёт и нужно открыть часть альвеолярных
капилляров. В любом случае срабатывает информатор лёгочного кровообращения и
блок управления решает, какую часть капилляров нужно открыть или закрыть.
Отсюда, диффузионная часть сосудистого русла лёгких является системой,
содержащей простой блок управления.
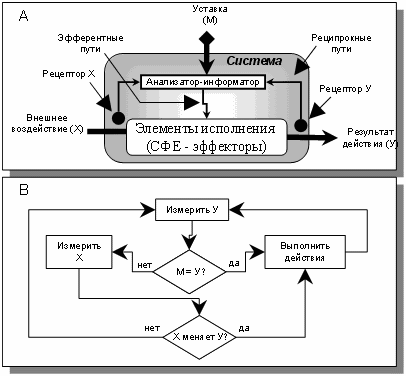
Рис. 9. Простой блок управления систем с ООС (А) и алгоритм его работы (В)
.
Цель системы - результат действия «Y» должен быть равен уставке «М» (Y=M).
Действия системы для достижения цели осуществляют элементы исполнения. Блок
управления следит за правильностью выполнения действий.
Блок управления, содержащий ППС и петлю ООС, является простым.
Алгоритм работы простых блоков управления не отличается большой сложностью (рис.
9). Петля ООС постоянно отслеживает результат действия исполнительных элементов
(СФЕ). Если результат действия получается больше, чем задано, нужно его
уменьшить, если результат меньше заданного – нужно его увеличить. Через уставку
задаются параметры управления («база данных»), например, каким должно быть
соотношение между внешним воздействием и результатом действия, или какой уровень
результата действия нужно постоянно удерживать и т.д. При этом максимальной
точностью будет результат действия одной СФЕ (квант действия).
Системы с ООС, как и составные СФЕ, также содержат два типа объектов:
элементы исполнения (СФЕ) (эффекторы, которые выполняют специфические
действия для достижения заданной генеральной цели системы)
блок управления (ППС и петля ООС)
Но блок управления системы кроме информатора «Х» также содержит и информатор
«У» (ОСС). Поэтому у него есть информация и о внешнем воздействии, и о
результате действия. Небольшое усложнение блока управления приводит к очень
существенному результату. Причина усложнения – необходимость получения
оптимально точного выполнения цели системы. ООС даёт возможность регуляции
количества результата действия, т.е., система с ООС может оптимально
выполнить любое необходимое действие, от минимума до максимума с точностью до
одного кванта действия.
Вообще говоря, в любой реальной системе есть ещё и третий тип объектов:
элементы обслуживания – вспомогательные элементы, без которых элементы
исполнения не смогут работать. Например, у самолёта есть крылья для того, чтобы
летать, но у него есть также и колёса, чтобы взлетать и садиться. Молекула
гемоглобина содержит гем, который содержит 4 СФЕ (лиганды) и глобин – белок,
который прямо не участвует в переносе кислорода, но без которого гем не сможет
работать. Основной СФЕ системы внешнего газообмена является ФЕВ – функциональная
единица вентиляции (функционально объединённая группа альвеол). Но без сервисных
систем (системы вентиляции, распределения, очистки и кондиционирования воздуха и
т.д.) ФЕВ не смогут нормально функционировать.
Мы слегка коснулись вопроса существования третьего типа объектов (элементов
обслуживания) только для того, чтобы знать, что они всегда присутствуют в любой
системе, но подробно рассматривать их функции мы не будем, чтобы не загромождать
наши рассуждения. Отметим только, что они представляют такие же обычные системы
с целью обслуживать другие системы.
Системы с ООС могут решать большинство задач намного лучше, чем простые или
составные СФЕ. Наличие ООС почти не усложняет систему. Мы видели, что уже
простая СФЕ является очень сложным образованием, включающим в себя множество
компонентов. Составная СФЕ сложнее простой СФЕ на число раз, почти равное числу
простых СФЕ в ней.
В системе с ООС добавляется всего лишь один рецептор и линия связи между
рецептором и анализатором (реципрокный путь). Но эффект от такого изменения
структуры блока управления очень большой и он зависит только от алгоритма работы
блока управления. Любая СФЕ (простая и составная) может выполнить только
минимум или максимум действия. Системы с ООС уже могут дать
оптимум результата действия, от минимума до максимума, являются точными и
стабильными. Их точность зависит только от величины кванта действия отдельной
СФЕ и глубины ООС (см. ниже). Стабильность обусловлена тем, что система
постоянно «видит» свой результат действия, может сравнивать его с должным и
исправлять его, если есть расхождение. В реальных системах всегда есть причины
для расхождения, потому что они существуют в реальном мире, где всегда есть
возмущающие воздействия. Отсюда видно, что именно ООС превращает СФЕ в настоящие
системы.
Каким образом блок управления управляет системой? Какие параметры его
характеризуют? Любой блок управления характеризуется тремя параметрами ППС и
столько же параметров петли ООС. Для ППС это:
- минимальным уровнем контролируемого входного воздействия (порог
чувствиетльности)
- максимальным уровнем контролируемого входного воздействия (диапазон
чувствительности входного воздействия)
- временем включения управления (временем принятия решения)
Для петли ООС это:
минимальным уровнем контролируемого результата действия (порог
чувствительности петли ООС - глубина ООС)
максимальным уровнем контролируемого результата действия (диапазон
чувствительности результата действия)
временем включения управления (временем принятия решения)
Минимальный уровень контролируемого входного сигнала для ППС – это
порог чувствительности сигнала рецептора «Х», начиная с которого
анализатор-информатор распознаёт, что внешнее воздействие уже началось.
Например, если рО2 достигло 60 мм Hg, то должен быть открыт сфинктер
(срабатывает 1 СФЕ), если меньше – закрыт. Любые значения рО2,
меньшие чем 60 мм Hg не приведут к открытию сфинктера, потому что они
подпороговые. Следовательно, 60 мм Hg являются порогом срабатывания сфинктера.
Максимальный уровень контролируемого входного сигнала (диапазон) для ППС
– это уровень сигнала о внешнем воздействии, при котором срабатывают все СФЕ. На
дальнейшее увеличение входного сигнала система же не может реагировать
увеличением своей функции, потому что у неё нет больше резервов СФЕ. Например,
если рО2 достигло 100 мм Hg, то должны быть открыты все сфинктеры
(срабатывают все СФЕ). Любые значения рО2, большие чем 100 мм Hg не
приведут к открытию даполнительных сфинктеров, потому что они все уже открыты.
Т.е., 60-100 мм Hg являются диапазоном срабатывания системы сфинктеров.
Время включения ППС – промежуток времени между началом внешнего
воздействия и началом срабатывания системы. Система никогда не срабатывает
мгновенно после появления внешнего воздействия. Пока рецепторы почувствуют
сигнал, пока анализатор-информатор примет решение, пока эффекторы передадут
управляющее воздействие на входы уставок исполнительных элементов, на всё это
уходит время.
Минимальный уровень контролируемого выходного сигнала для ООС –
это порог чувствительности сигнала рецептора «У», начиная с которого
анализатор-информатор распознаёт, что есть расхождение между результатом
действия системы и его должной величиной. Расхождение должно быть равно или
больше кванта действия одиночной СФЕ. Например, если должен быть открыт один
сфинктер и кровоток должен быть минимальным (один квант действия), а на самом
деле открыто два сфинктера и кровоток в два раза больше (два кванта действия),
то рецептор «У» должен почувствовать лишний квант. Если он может это сделать, то
его чувствительность равна одному кванту. Чувствительность определяется глубиной
ООС.
Глубина ООС – это число квантов действия одиночных СФЕ системы, сумма
которых распознаётся как расхождение между актуальным результатом действия и
должным. Задаётся уставкой. Максимально большой глубиной ООС является
чувствительность расхождения в один квант действия одиночной СФЕ. Чем меньше
глубина ООС, тем меньше чувствительность, тем она более «грубая». Т.е., чем
меньше глубина ООС, тем большее расхождение результата действия с должным
воспринимается как расхождение. Например, уже два (три, десять и т.д.) кванта
действия двух (трёх, десяти и т.д.) СФЕ воспринимается как расхождение.
Минимальной глубиной ООС является её отсутствие. В этом случае любое расхождение
результата действия с должным не воспринимается блоком управления как
расхождение. Результат действия будет максимальным и система с простым блоком
управления с нулевой глубиной ООС превращается в составную СФЕ с ППС (с
простейшим блоком управления).
Например, система микроциркуляции БКК в тканевых капиллярах должна держать
среднее давление 100 мм Hg с точностью до 1 мм Hg. При этом среднее артериальное
давление может колебаться от 80 до 200 мм Hg. Величина «100 мм Hg» определяет
уровень контролируемого результата действия. Величина «от 80 до 200 мм Hg»
диапазон контролируемого внешнего (входного) воздействия.
Величина «1 мм Hg» определяется глубиной ООС. Меньшая глубина ООС будет
контролировать параметр с меньшей точностью, например с точностью до 10 мм Hg
(более грубо) или 50 мм Hg (ещё грубее), а большая глубина ООС – с большей
точностью, например с точностью до 0.1 мм Hg (более тонко). Максимальная
чувствительность ООС ограничена величиной кванта действия СФЕ, входящих в состав
системы и глубиной ООС. Но в любом случае если происходит расхождение уровня
контролируемого параметра с заданным более, чем на величину заданной точности,
петля ООС должна «почувствовать» это расхождение и «заставить» исполнительные
элементы действовать таким образом, чтобы расхождение цели и результата действия
исчезло.
Максимальный уровень контролируемого выходного сигнала (диапазон) для ООС
– это уровень сигнала о результате действия системы, при котором срабатывают все
СФЕ. На дальнейшее увеличение входного сигнала система же не сможет реагировать
увеличением своей функции, потому что у неё нет больше резервов СФЕ.
Время включения управления ООС – промежуток времени между началом
расхождения сигнала о результате действия с целевым и началом срабатывания
системы.
Все эти параметры могут быть «встроены» в ППС и в петли ООС либо изначально (уставка
вводится при их «рождении») и в дальнейшем они уже не меняются. Либо могут быть
введены с уставкой позже и эти параметры можно менять путём ввода извне новой
уставки. Для этого должен быть канал ввода уставки. Сам же простой блок
управления сам не может менять ни один из этих параметров.
Абсолютно у всех систем есть блок управления, но не всегда его можно явно
обнаружить. У самолёта или космического корабля этим блоком является бортовой
компьютер – коробка с электроникой. У человека и других животных таким блоком
является головной мозг, или как минимум – нервная система. Но где блок
управления у растения, или у бактерии? Где блок управления у атома или молекулы,
или, например, блок управления у гвоздя?
Чем проще система, тем труднее выделить в нём привычные для нас формы блока
управления. Но он есть в любых системах. Элементы исполнения отвечают за
качество результата дейсвтия, а блок управления – за его количество. Блоком
управления могут быть, например, внутри- или межатомные и межмолекулярные связи.
Так в атоме функции СФЕ выполняют электроны, протоны и нейтроны, а блок
управления– внутриядерные силы, или, как ещё говорят, взаимодействия.
Внутриатомной уставкой, например, является условие, что на первом электронном
уровне может быть не более 2 электронов, на втором – 8 электронов и т.д.
(периодический закон, определяемый принципом Паули), причём этот уровень жестко
задан квантовыми числами. Если электрон каким-то образом получил добавочную
энергию и поднялся выше своего уровня, то он не сможет её долго удерживать и
опустится обратно, испустив излишек энергии в виде фотона. Причём не любая
энергия может поднять электрон на другой уровень, а только и только определённая
(соответствующий квант энергии). И поднимается он не на любой уровень, а только
на строго заданный. Если энергия внешнего воздействия будет меньше
соответствующего кванта, система стабилизации уровня электрона будет удерживать
его на прежней орбите (в прежнем состоянии) до тех пор, пока энергия внешнего
воздействия не превысит соответствующий уровень. Если же энергия внешнего
воздействия будет всё время линейно нарастать, то электрон будет подниматься с
уровня на уровень не линейно, а перескакивать скачками, которые строго
определены квантовыми законами, на всё более высокие орбиты, как только энергия
воздействия превысит определённые пороговые уровни. Число уровней орбиты
электрона в атоме, вероятно, очень большое и равно числу спектральных линий
соответствущего атома, но каждый уровень строго фиксирован и определён
квантовыми законами. Следовательно, какой-то механизм (система стабилизации
квантовых уровней) строго следит за выполнением этих законов, и у этого
механизма должны быть свои СФЕ и блоки управления. Число уровней орбиты
электрона, вероятно, определяется числом внутриядерных СФЕ (протонов и нейтронов
или же других элементарных частиц), результатом действия которых является
положение электрона на электронной орбите.
Например, у гвоздя уставкой, являются его форма и геометрические размеры. Эта
уставка вводится в блок управления однократно в момент изготовления гвоздя,
когда отмеряются его размеры (в момент его «рождения»), и больше уже не
вводится. Но когда уставка уже введена, то система должна выполнять эту уставку,
т.е., в данном случае гвоздь должен держать форму и размеры, даже если по нему
бьют молотком. В любых типах блока управления в какой-то момент должна быть
введена уставка тем или иным образом. Мы не можем изготовить гвоздь «вообще», а
только конкретной формы и заданных размеров. Поэтому, в момент его изготовления
(т.е., однократно) мы «задаём» ему задание быть такой-то формы и размеров.
Уставка может меняться, если есть канал ввода уставки. Например, при
включении кондиционера воздуха, мы можем «задать» ему держать температуру
воздуха 20°С, а затем поменять уставку на 25°С. У гвоздя нет канала ввода
уставки, а у кондиционера есть.
Таким образом, система с простым блоком управления является объектом,
который может реагировать на определённое внешнее воздействие, а результат её
действия градуированный и стабильный. Число градаций определяется числом СФЕ в
системе, а точность – квантом действия одиночной СФЕ и глубиной ОСС. Результат
действия точный потому, что блок управления контролирует его с помощью ООС. Тип
управления – по рассогласованию. Управление начинается только после появления
внешнего воздействия или результата действия. Стабильность результата действия
определяется глубиной ООС. Реакция системы обусловлена типом и числом её СФЕ.
У простого блока управления есть три канала управления – один внешний (уставка)
и два внутренних (ППС и ООС). Он реагирует на внешнее воздействие через ППС
(информатор «Х») и на собственный результат действия системы (информатор «У»)
через ООС, а через эфферентные пути управляет исполнительными элементами
системы.
Аналогом систем с простым блоком управления являются все объекты неживого
мира – газовые облака, кристаллы, различные твёрдые тела, планеты, планетарные и
звёздные системы и т.д.
Биологическим аналогом систем с простым блоком управления являются одно- и
многоклеточные растения, бактерии и все вегетативные системы организма, включая,
например, систему внешнего газообмена, систему кровообращения, систему обмена
метаболических газов, систему пищеварения или иммунную систему.
Одноклеточные животные организмы типа амёб и инфузорий, низшие классы
животных (медузы и пр.) уже являются системами с сложными блоками управления
(см. далее).
Все вегетативные и многие двигательные рефлексы высших животных,
срабатывающие на всех уровнях, начиная с интрамуральных нервных ганглиев и
вплоть до гипоталамуса, построены по типу простых блоков управления. Если же на
них оказывается управляющее влияние коры головного мозга, то появляются рефлексы
более высокого типа – сложные рефлексы (см. ниже).
Аналогом рецепторов информатора «Х» являются все чувствительные рецепторы
(хемо-, баро-, термо- и прочие рецепторы, расположенные в различных органах,
кроме зрительных, слуховых и обонятельных рецепторов, которые входят в состав
информатора «С», см. далее).
Аналогом рецепторов информатора «У» являются все проприо-чувствительные
рецепторы, которые также могут быть хемо-, баро-, термо- и прочими рецепторами,
расположенные в различных органах.
Аналогом стимуляторов блока управления являются все двигательные и
эффекторные нервы, стимулирующие поперечно-полосатую, гладкомышечную мускулатуру
и секреторные клетки, а также гормоны, протогландины и прочие метаболиты,
оказывающие какое-либо влияние на функцию каких-либо систем организма.
Аналогом анализатора-информатора в минеральном и растительном мирах являются
только связи между элементами по типу прямого соединения информаторов «X» и «У»
с эффекторами (аксон-рефлексы). В вегетативных системах животных – также по типу
типу прямого соединения информаторов «X» и «У» с эффекторами (гуморальная и
метаболическая регуляция), по типу аксон-рефлекса (управляют только веточки
нерва без участия самой нервной клетки) и по типу безусловных рефлексов (на
уровне внутриорганных интрамуральных и других нейронных образований вплоть до
гипоталамуса).
Таким образом, используя ППС и ООС и регулируя работу своих СФЕ система
продуцирует свои результаты действия, качественно и количественно
соответствующие заданной цели.
Принцип независимости результата действия.
Как уже неоднократно подчеркивалось, целью любой системы является получение
должного (целевого) результата действия, который получается после действий
системы. Фактически внешнее воздействие, «войдя» в систему преобразуется в
результат действия системы. Поэтому системы фактически являются
преобразователями внешнего воздействия в результат действия, причины в
следствие. А внешнее воздействие является результатом действия другой системы,
которая взаимодействовала с данной. Следовательно, результат действия, «выйдя»
из одной системы и «войдя» в другую, существует уже независимо от системы его
породившей.
Например, у строительной фирмы была цель из определённого количества
строительного материала (внешнее воздействие) построить дом. После ряда действий
этой фирмы дом оказался построен (результат действия). Далее фирма могла перейти
к строительству другого дома, прекратить свое существование или
переквалифицироваться в из строительной в пошивочную фирму. Но построенный дом
уже будет существовать независимо от построившей его фирмы.
Целью автомобильного мотора (подсистемы автомобиля) является сжигание
определённого количества горючего (внешнее воздействие для мотора) для получения
определённого количества механической энергии (результат действия мотора). Целью
ходовой части (другой подсистемы автомобиля) является преобразование
механической энергии мотора (внешнее воздействие для ходовой части) в
определённое количество оборотов колёс (результат действия ходовой части). Целью
колёс является преобразование определённого числа их оборотов (внешнее
воздействие для колёс) в пройденные километры пути (результат действия колёс). В
целом, результатом действия автомобиля будут пройденные километры пути, которые
уже будут существовать независимо от проехавшего по ним автомобиля.
Результатом действия возбуждённого электрона будет выпущенный из атома фотон,
который может бесконечно блуждать по просторам Вселенной на протяжении многих
миллиардов лет. Результатом шлепка весла о воду является ямка на воде, которая
также могла бы остаться на века, если бы не текучесть воды и не воздействие на
неё тысяч других внешних воздействий. Однако после тысячи воздействий она
останется уже не в виде ямки, а в виде другой длинной цепи результатов действий
других систем, потому что ничто в этом мире не исчезает, а переходит в другие
формы. Закон сохранения нерушим.
Циклы системы и переходные процессы.
У систем, как и у СФЕ, также есть циклы их деятельности. У разных систем
могут быть разные циклы деятельности и они зависят от сложности и алгоритма
блока управления. Самый простой цикл работы у системы с простым блоком
управления. Он складывается из микроциклов (рис. 10):
восприятие, селекции и измерения внешнего воздействия рецептором «X»
выбор из «базы данных» должного значения результата действия
переходный процесс (мультимикроцикл ООС)
a. восприятие и измерение результата действия рецептором «Y»
b. сравнение этого результата с с должной величиной
c. выработка решения и соответствующего воздействия на СФЕ с целью
коррекции результата действия
d. воздействие на СФЕ если результат действия не равен должному, или
переход к 1-му микроциклу, если он равен должному
e. срабатывания СФЕ
f. возврат к «а»
После начала внешнего воздействия срабатывает рецептор «X» (1-й микроцикл).
Затем из «базы данных» выбирается то значение результата действия, которое
должно соответствовать данному внешнему воздействию (2-й микроцикл). После этого
начинается переходный процесс (переходный период, 3-й мультимикроцикл, цикл ООС):
срабатывание рецептора «Y», сравнение результата действия с должной величиной,
выбранной в «базе данных», корректирующее воздействие на СФЕ (включаются то
число СФЕ, которое определил блок уравления в микроцикле «с») и снова возврат к
срабатыванию рецептора «Y». И так до тех пор, пока результат действия не будет
равным данному. С этого момента цель достигнута и после этого блок управления
возвращается к 1-му микроциклу, к рецепции внешнего воздействия. Деятельность же
системы для выработки результата действия прекращается до тех пор, пока не
появится новое внешнее воздействие.
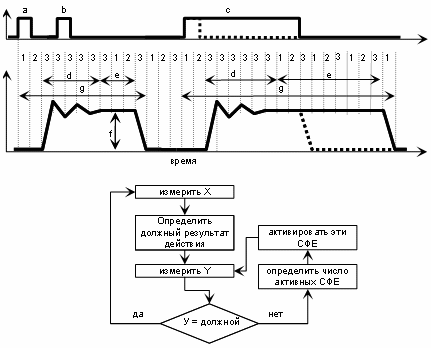
Рис. 10. Полный цикл действия идеальной системы и алгоритм её работы. На
верхней кривой – внешнее воздействие, на нижней – график функции системы.
Цифрами (1. 2, 3) указаны микроциклы системы.
a – внешнее воздействие, на которое система начинает реагировать; b –
внешнее воздействие, на которое система не реагирует, потому что находится в
рефрактерном состоянии (не может активировать свои СФЕ, потому что не измеряет
Х); с – длительное внешнее воздействие, на которое система реагирует (пунктиром
показана реакция системы, если бы длительность внешнего воздействия была
прежней); d – переходный мультицикл системы; е – установившееся значение
функции; f – заданное значение результата действия системы; g – полный цикл
действия системы.
1 – восприятие и селекция внешнего воздействия рецептором «X» после начала
внешнего внешнего воздействия; 2 – выбор из «базы данных» должного значения
результата действия; 3 - мультимикроцикл ООС; 4 – время установившегося целевого
уровня функции; 5 – прекращение функции.
К выше сказанному следует добавить очень существенное дополнение. При
рассмотрении циклов срабатывания СФЕ уже указывалось, что после срабатывания
любой СФЕ она полностью расходует свой запаса энергии, предназначенный для
производства действия. Поэтому после завершения действия СФЕ не способна
совершать новое действие до тех пор, пока она не восстановит свой энергетический
потенциал, а на это уходит дополнительное время, которое может существенно
увеличить длительность переходного периода. Поэтому у спортсмена, у которого
система доставки кислорода в ткани велика (большая скорость поставки энергии),
скорость движения тела, например, бега, также велика. А у сердечного больного
скорость движения тела низкая, потому что скорость поставки энергии снижена
из-за поражения системы кровообращения, которая входит в состав системы
энергоснабжения организма. У больных много времени уходит на восстановление
энгергетического потенциала мышечных клеток из-за замедленной продукции АТФ,
требующей много кислорода.
Микроциклы с 1-го по 2-й составлят стартовый период работы блока
управления. Если было короткое внешнее воздействие, блок управления определяет
его во время стартового цикла и переходит к переходному периоду (d на
рис. 10), во время которого стремится получить актуальный результат действия,
равный должному. Если во время переходного периода снова появится внешнее
воздействие (b на рис. 10), то блок управления не прореагирует на него, потому
что в этот момент он не измеряет «Х» (рефрактерная фаза). По окончании
переходного периода блок управления вновь обращается к стартовому периоду, но
пока он это делает (обращается), достигнутое должное значение результата
действия сохраняется неизменным (установившийся период).
Если внешнее воздействие достаточно длительно и не менется, так что после
первого достижения цели блок управления успевает вновь обратиться к рецепции
«Х», то установившееся значение результата действия будет сохраняться до тех
пор, пока будет продолжаться внешнее воздействие. При этом переходного цикла не
возникнет, потому что установившееся значение результата действия равно
должному.
Если длительное внешнее воздействие будет продолжаться и менять свою
амплитуду, то возможно появление нового переходного цикла. Причём амплитуда
колебаний функции будет тем больше, чем больше изменение амплитуды внешнего
воздействия. Поэтому резкие перепады амплитуды внешнего воздействия недопусимы,
потому что они вызывают различны нежелательные эффекты, связанные с переходным
периодом рис. 11).
Если внешнее воздействие будет равно нулю, то все СФЕ дезактивируются, потому
что нулевому внешнему воздействию соответствует нулевая активация СФЕ.
Если спустя некотрое время появится новое внешнее воздействие, то система
повторит всё в прежнем порядке.
На длительность цикла работы системы также существенное влияние оказывают
процессы восстановления энергетического потенциала сработавших СФЕ. Каждая СФЕ
при своём срабатывании затрачивает определённое (квантованное) количество своей
энергии, которая либо привносится самим внешним воздействием, либо накапливается
какими-либо подсистемами энергоснабжения данной системы. В любом случае
восстановление энергетического потенциала также требует времени, но эти процессы
мы не рассматриваем, потому что эти процессы касаются только элементов
исполнения (СФЕ), а мы рассматриваем только процессы, происходящие в блоках
управления систем.
Так система постоянно циклически работает, выполняя свои микроциклы. Если нет
внешнего воздействия или оно не меняется, то система находится на одном из своих
стационарных уровней в одном и том же функциональном состоянии с одним и тем же
числом функционирующих СФЕ, от нуля до всех. В таком режиме у неё нет
переходного мультимикроцикла (длительного повтора 3-го микроцика).
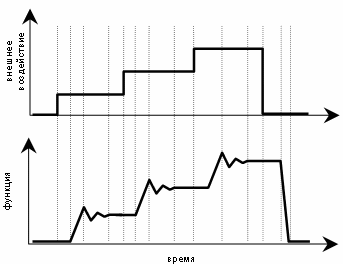
Рис. 11. График функции системы при меняющемся уровне внешнего
воздействия.
При каждом изменении уровня внешнего воздействия возникают переходные
процессы. Переход функции на новый уровень становится возможным лишь после того,
когда система готова это сделать.
У разных систем подобные микроциклы могут отличаться в деталях, но у всех без
исключения систем есть мультимикроцикл ООС. При всех достоинствах ООС у неё есть
очень существенный недостаток – наличие переходных процессов. Выраженность
переходных процессов зависит от очень многих факторов. Она может быть от
минимальной до максимальной, но переходные процессы всегда есть у всех систем в
той или иной степени выраженности. Они неустранимы принципиально, потому что ОСС
срабатывает уже после появления результата действия системы. Пока аффекторы
системы почувствуют рассогласование, пока блок управления примет соответствующее
решение, пока эффекторы исполнят это решение, пока ООС измерит результат
действия и подправит решение, и пока этот процесс повторится несколько раз до
тех пор, пока не будет получено нужное соотношение «...внешнее воздействие →
результат действия...», пройдёт некоторое время. Поэтому в это время могут
возникнуть всякие неожидаемые нелинейные переходные процессы, нарушающие
нормальный режим работы системы. Поэтому при первом «включении» системы в
действие или при резкой смене нагрузки ей нужен достаточно длительный период
установления. И даже в установившемся режиме из-за различных случайных
флюктуаций во внешней среде может быть небольшой сбой в работе ООС и могут
появляться небольшие переходные процессы («шум» результата действия реальной
системы).
Наличие переходных процессов накладывает определённые ограничения на работу и
область использования систем. Медленные иннерционные системы не подходят для
быстрых внешних воздействий, потому что быстродействие систем в первую очередь
определяется быстродействием петли ООС. Да, быстродействие исполнительных
элементов является основой быстродействия системы в целом, но мультимикроцикл
ООС вносит свою существенную долю в удлинение цикла работы системы. Поэтому при
выборе нагрузок на живой организм необходимо учитывать быстродействие системы и
подбирать скорость нарастания нагрузок таким образом, чтобы выраженность
переходных процессов была наименьшей.
Чем медленнее меняется внешнее воздействие, тем меньше переходный процесс
(рис. 12). При достаточно медленном изменении внешнего воздействия переходный
период становится практически незаметным. Следовательно, если внешнее
воздействие меняется, то в зависимости от скорости этого изменения и от
быстродействия элементов системы длительность переходного периода может быть от
нуля до максимально возможного.
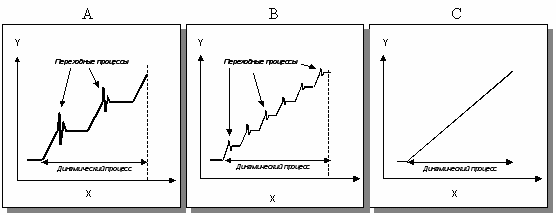
Рис. 12. Переходные процессы.
Переходный процесс – это процесс перехода с одного уровня функционального
состояния на другой. Чем «мельче» ступеньки перехода с одного уровня на другой,
тем меньше амплитуда переходных процессов (А и В). При плавном изменении
нагрузки нет переходных процессов (С).
Выраженность переходных процессов зависит от калибра СФЕ, силы внешнего
воздействия, от времени зарядки энергией СФЕ, от чувствительности рецепторов, от
времени их срабатывания, от глубины ОСС и от алгоритма работы блока управления.
Но эти циклы работы систем и переходные процессы есть и внутри атомов, и в
электронных схемах, и в планетарных системах, и во всех остальных системах,
наполняющих наш Мир, включая организм человека.
Если бы у систем не было переходных процессов, то время переходного периода
всегда было бы равно нулю и системы были бы абсолютно безинерционными. Но таких
систем нет и любой системе присуща инерционность в той или иной степени.
Например, в электронике наличие переходных процессов порождает дополнительные
гармоники колебаний электрического тока в различных усилителях или генераторах
тока. Для их подавления применяются изощренные схемные решения, но они есть в
любых электронных приборах, хотя и значительно подавленные.
Постоянная времени систем с простыми блоками управления включает
постоянные времени каждой СФЕ плюс непостоянные длительности переходных периодов
ООС. Поэтому постоянная времени таких систем не совсем постоянная, потому что
длительности переходных периодов ООС могут меняться в зависимости от силы
внешнего воздействия. Переходные процессы в системах с простыми блоками
управления увеличивают иннерционность таких систем.
Инерционность систем приводит к различным фазовым нарушениям синхронизации и
баланса взаимодействия между системами. Бороться с переходными процессами можно
очень многими способами. Можно фильтровать внешние воздействия таким образом,
что бы не было резких ударных воздействий (фильтрация, принцип постепенности
нагрузки). Если заранее знать характер внешних воздействий, предвидеть их, для
чего нужно их сначала увидеть, что под силу как минимум только сложным блокам
управления, то можно построить такой соответствующий алгоритм работы блока
управления, чтобы 3-й микроцикл сразу нашел верное решение (управление по
упреждению). Но это подсильно только лишь интеллектуальным блокам управления.
Полностью избавиться от инерционности систем, нам пока, видимо, не удаётся.
Поэтому если внешнее воздействие не меняется и переходные процессы
практически равны нулю, то система циклически и ровно работает на одном из своих
стационарных уровней. Или гладко переходит с одного стационарного уровня на
другой, если внешнее воздействие меняется, но достаточно медленно. Если
переходные процессы становятся ощутимыми, то циклы работы системы становятся
неравными из-за появления переходных мультимикроциклов – времени переходных
процессов. Нелинейные эффекты при этом снижают эффективность работы системы.
В нашей обыденной жизни мы часто сталкиваемся с переходными процессами, когда
совершенно неподготовленные выходим из тёплой комнаты на холод и получаем
простуду. В тёплой комнате все системы нашего организма были в определённом
балансе своих взаимодействий и всё было нормально. Но вот мы вышли на холод и
все системы должны сразу же перестроиться на новый баланс. Если они не успевают
это сделать, если возникают слишком сильные переходные процессы, при которых
появляются неожидаемые флюктуации результатов действий систем организма, то
возникает дисбаланс взаимодействий систем, который мы называем простудой (здесь
мы не уточняем частности, связанные с изменением состояния иммунной системы).
Спустя некоторое время дисбаланс ликвидируется и простуда проходит. Если мы
будем закаляться, то сможем научить наши «блоки управления», как предвидеть
резкие удары внешних воздействий, чтобы уменьшить переходные процессы, тогда мы
сможем даже купаться в проруби.
Особое значение для нас имеют переходные процессы, возникающие при резкой
смене ситуации вокруг нас. Стресс-синдром прямо связан с этим явлением. Чем
резче меняется ситуация вокруг нас, чем она более угрожающая (чем сильнее
внешнее воздействие), тем резче переходные процессы, вплоть до парадоксальных
реакций типа ступора. При этом возникает дисбаланс работы различных участков
нервной системы (блоков управления), который приводит к дисбалансу работы
различных систем организма и появлению различных патологических реакций и
процессов, типа вегетоневрозов и депрессий, ишемий вплоть до инфарктов и язв,
начиная с ротовой полости (афты) и до толстого кишечника (явенные колиты, язвы
желудка и 12-ти перстной кишки и т.д.), артериальной гипертонии и т.д.
Цикличность – это свойство систем не только живого организма. Любая система
работает циклически. Если внешнее воздействие сохраняется на стабильном уровне,
то работает этот минимальный установившийся цикл работы системы. Но и внешнее
воздействие также может меняться циклически, например, от сна ко сну, от обеда
до обеда и т.д. Это уже вторичные, третичные и т.д. циклы. Если построить
графики функций системы, то получим волнообразные кривые, характеризующие
цикличность. Примерами этому могут быть кривые пневмотахограммы,
электрокардиограммы, кривые изменения кислотности желудочного сока,
сфигмограммы, кривые электрической активности нейронов, периодичность
альфа-ритма ЭЭГ и т.д.
Волны на море, смена времён года, движения планет, движения поездов и т.д.,
всё это примеры цикличности различных систем. Формы кривой цикличности могут
самыми разнообразными. Кривая ЭКГ отличается от кривой артериального давления, и
кривая артериального давления отличается от кривой давления в левом желудочке.
Число форм кривых безгранично.
Два основных параметра характеризуют цикличность – период (или
обратная периоду величина – частота) и неравномерность периода, в
понятие которой входит понятие гармоник частоты. У СФЕ (простейшая
система) не должно быть неравномерности периода цикла, её циклы действия всегда
одинаковы. Но у систем уже есть переходные периоды, у которых может быть
различное время цикла. Кроме того, различные системы имеют собственные периоды
цикла и при их взаимодействии происходит интерференция (наложение) периодов.
Поэтому появляются дополнительные смещения собственных периодов систем,
появляются гармоники циклов.
Кровенаполнение лёгких определяется в основном балансом синхронности и
соразмерности ударного выброса правого и левого желудочков сердца (баланс
притока и оттока лёгочного объёма крови). Но на кровенаполнение лёгких также
оказывают влияние дыхательные движения грудной клетки, которые меняют давление
внутри альвеол и, тем самым, сдавливая лёгочные сосуды, меняют их сопротивление.
Период сердечных циклов порядка 1- 0.25 секунды, а период дыхания в 3-4 раза
больше. Соответственно на кривой кровенаполнения лёгких можно увидеть и
кардиоциклы, и циклы дыхания (рис. 13, кривая импедансной реоплетизмографии
лёгких в модификации тетраполярной реоплетизмографии по Кубичеку).
Число таких наложений волн может быть сколь угодно большим. Поэтому реально
мы наблюдаем очень большое разнообразие кривых – правильные синусоиды,
неправильные кривые и т.д. Но любые кривые можно разложить на составляющие их
волны, т.е., разложить интерференцию на её составляющие, используя специальные
методы анализа, например, преобразования Фурье. В результате можно получить
спектр более простых волн типа синусоиды. Чем более детальный (и одновременно
более трудоёмкий) анализ, тем ближе форма каждой составляющей к синусоиде и тем
большее число синусоидальных волн с разным периодом.
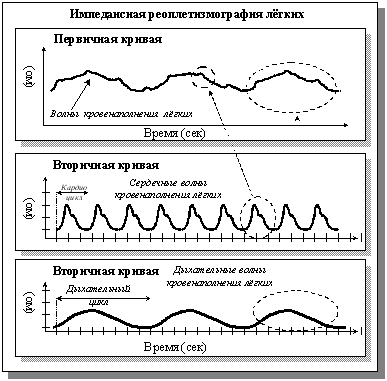
Рис. 13. Дыхательные и сердечные волны (циклы) кровенаполнения лёгких.
На верхнем графике представлена полная импедансная реоплетизмограмма
лёгких, представляющая собой сумму волн сердечных и дыхательных циклов (обведены
пунктирными кружками). На среднем графике – кардиоциклы, после фильтра нижних
частот, срезающих низкочастотные дыхательные волны. На нижнем графике –
дыхательные волны, после фильтра верхних частот, срезающего высокочастотные
кардиоволны.
Период цикла системы – очень важный параметр для понимания процессов,
происходящих в любой системе, в том числе и в живом организме. Его длительность
зависит от постоянной времени реакции системы на внешнее воздействие. Начав
очередной цикл действий система не остановится, пока не закончит его. Можно
попытаться воздействовать на систему в то время, когда она ещё не закончила свой
цикл действий, но реакция системы на такое действие не будет адекватной.
Скорость нарастания функций системы полностью зависит от времени периода цикла
действий системы. Чем больше период цикла, тем медленнее система переходит от
уровня к уровню.
Понятия абсолютной и относительной рефрактерности прямо связаны
с понятием периода и фазы цикла системы (рис. 14). Если, например, миокард не
закончил свой цикл «систола-диастола», то внеочередной (преждевременный) импульс
водителя ритма или экстрасистолический импульс не сможет заставить желудочек
выдать полноценный ударный выброс. В зависимости от того, на какую фазу
рефрактерного периода придётся экстрасистолический импульс, величина ударного
выброса может меняться от нуля до максимально возможного. Если возбуждающий
импульс попадёт на на 2-й и 3-й микроциклы, миокард вообще не прореагирует на
них (абсолютная рефрактерность), потому что во время не измеряется информация с
рецептора «X». После сокращения миокарду, как и любой другой клетке после её
возбуждения, требуется некоторое время для восстановления энергетического
потенциала (накопление АТФ) и для установки всех СФЕ в «стартовое» состояние.
Если в это время появится внеочередной импульс, то ответ системы возможен в
зависимости от того, сколько АТФ уже накопилось или в какой степени разошлись
акто-миозиновые нити саркомеров миокарда, чтобы снова включиться в функцию
(относительная рефрактерность).
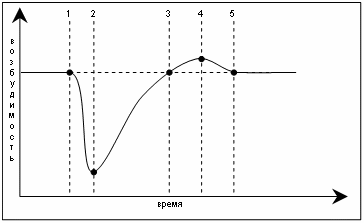
Рис. 14. Рефрактерные фазы возбудимости живых тканей.
Возбудимость невозбуждённой клетки наибольшая. В момент её возбуждения (1)
возбудимость резко падает до нуля (2, все СФЕ в действии, 2-й микроцикл) –
абсолютная рефрактерность. Затем, если нет последующего возбуждения, система
постепенно восстанавливает свою возбудимость, проходя через фазы относительной
рефрактерности, до первоначальной (3) и даже выше (сверхвозбудимость, в рамках
данной книги не рассматривается), и затем снова до первоначального уровня (4).
Поэтому у больных сердечной недостаточностью может наблюдаться
неравномерность пульса, когда пульсовые толчки неравномерны по силе. Крайним
проявлением такой неравномерности является так называемый «дефицит пульса» –
есть электрическая активность сердца на ЭКГ, но нет её механического
(гемодинамического) аналога на сфигмограмме и при пальпации пульса ударного
толчка не ощущаем.
Главные выводы из всего выше сказанного:
любые системы работают циклически, проходя через микроциклы
у любой системы есть переходные процессы
период цикла у каждой системы может быть различен и зависит от постоянной
времени реакции системы на внешнее воздействие (в живых системах – от скорости
биохимических реакций и от скорости проведения управляющих сигналов)
неравномерность периода цикла системы зависит от наличия переходных
процессов, следовательно, в определённой степени, от силы внешнего воздействия
неравномерность периода цикла системы зависит от наложения периодов циклов
взаимодействующих систем
по окончании цикла действий после одиночного воздействия система
возвращается в исходное состояние, в котором она была до начала внешнего
воздействия (на одиночное внешнее воздействие – одиночный результат действия).
Последнее (6) не касается так назывемых генерирующих систем. Это связано с
тем, что после того, как результат действия был произведен системой, он
становится независим от произведшей его системы и сам может стать внешним
воздействием для неё же. Если подать его на вход внешнего воздействия той же
системы, она опять возбудится и снова произведёт новый результат действия
(положительная обратная связь, ПОС). Так работают все генераторы.
Таким образом, если на систему оказывается первое внешнее воздействие, или
внешнее воздействие постоянно меняется, число функционирующих СФЕ системы
меняется. Если на систему не оказывается никакого внешнего воздействия или
это воздействие есть, но оно не меняется, то число функционирующих СФЕ системы
не меняется. Отсюда мы можем вывести определения стационарных состояний и
динамичности процесса.
Функциональное состояние системы.
Функциональное состояние системы определяется числом активных СФЕ. Если все
СФЕ одновременно функционируют – это максимально высокое функциональное
состояние, которое возникает при максимальном внешнем воздействии. Если ни одна
СФЕ не активна – это минимальное функциональное состояние. Это может быть при
отсутствии внешнего воздействия.
Внешняя среда постоянно оказывает какое-либо воздействие на любые системы,
включая системы организма. Даже в состоянии покоя сила земного притяжения
заставляет работать часть наших мышц, и поэтому нет абсолютного покоя. Таким
образом, когда мы как будто находимся в состоянии покоя, на самом деле мы
находимся на одном из низких уровней физической нагрузки с соответствующим
определённым низким уровнем функционального состояния организма. Любое внешнее
воздействие, требующее дополнительной активной деятельности, переводит на новый
уровень функционального состояния, если только резерв СФЕ не исчерпан. Когда
новое воздействие устанавливается на новом неизменном (стационарном) уровне, то
и функциональное состояние системы устанавливается в новом неизменном
(стационарном) функциональном уровне.
1. Стационарные состояния.
Стационарным является такое состояние систем, когда в этих системах
функционирует одно и то же число СФЕ и не происходит изменения их
функционального состояния.
Например, в состоянии покоя все системы организма не меняют своего
функционального состояния, поскольку всё время функционирует примерно постоянное
число СФЕ.

Рис. 15. Стационарные состояния покоя и бега в неизменном ритме.
В обоих случаях потребление кислорода (VO2) не меняется, хотя
во время бега этот параметр гораздо выше, чем в состоянии покоя.
Бегунья, которая бежит на длинной дистанции достаточно долгое время не меняя
скорости бега, также находится в стационарном состоянии (рис. 15). Её нагрузка
не меняется и поэтому не меняется число работающих (функционирующих) СФЕ, т.е.,
не меняется функциональное состояние её организма. Организм уже «вработался» в
эту не меняющуюся нагрузку, а поскольку нет прироста нагрузки, то нет и прироста
числа работающих СФЕ. Оно (число работающих СФЕ) сохраняется постоянным и
поэтому функциональное состояние организма не меняется. У данной бегуньи может
меняться, например, состояние систем тканевой энергопродукции (истощение запасов
гликогена) и систем тканевого энергопотребления (возможно истощение и износ
митохондрий, миофибрилл, саркоплазматического ретикулума и т.д.), что и является
процессом утомления организма. Однако, если бегунья правильно спланировала
тактику бега таким образом, чтобы не входить в состояние анаэробного обмена, то
состояние систем внешнего газообмена и кровообращения не меняется. Таким
образом, нет физической нагрузки, или она есть, но не меняется (стационарная
физическая нагрузки – steady state, при условии её адекватности возможностям
организма), организм субъекта будет находиться в стационарном состоянии.
Но если бегунья будет бежать в условиях анаэробного обмена, то начнёт
работать порочный круг (см. далее) и функциональное состояние её организма будет
неуклонно меняться в худшую сторону. Обычно прекращение нагрузки прерывает этот
порочный круг. Иногда, если испытуемый является тяжелым кардиологическим больным
в стадии сердечной декомпенсации, испытание даже очень малыми дозами физической
нагрузки «загоняет» его в анаэробный обмен и из-за кислородного долга ему уже
очень трудно из него выйти, что приводит к госпитализации больных со всеми
вытекающими отсюда последствиями. Это следует учитывать при проведении теста с
максимальными физическими нагрузками.
Таким образом, любые системы организма всегда находятся в одном из своих
сиюминутных стационарных состояний. Они переходят с одного уровня на другой
только в случае изменения внешнего воздействия. Можно говорить о диапазоне
различных стационарных состояний, в котором может меняться система. Например, в
состоянии покоя величина потребления кислорода организмом человека (VO2)
около 200 мл/мин, а в нагрузке VO2=2000 мл/мин. В лёгких человека
есть около 1.5 млн функциональных единиц вентиляции (ФЕВ), каждая из которых
представляет собой группу из примерно 200 альвеолярных ходов. Каждая из этих ФЕВ
может быть включена в вентиляцию, или отключена от неё, чтобы обеспечить
необходимый уровень VO2. Следовательно, в покое действуют только
около 120 тыс. ФЕВ, а в нагрузке все 1.2 млн.
2. Динамические процессы.
Динамическим процессом является процесс изменения функционального состояния
системы. Система находится в динамическом процессе тогда, когда происходит
изменение числа её СФЕ, включенных в действие. Число постоянно включенных в
действие СФЕ определяет стационарное состояние системы. Отсюда, динамический
процесс – это процесс перехода системы с одного стационарного уровня на другой.
Если скорость изменения внешних воздействий превышает скорость установления
заданного результата действия системы, то появляются переходные процессы (мультимикроциклы),
во время которых также происходит изменение числа функционирующих СФЕ. Поэтому
эти переходные процессы также являются динамическими.
Следовательно, есть два типа динамических процессов – когда система переходит
с одного своего стационарного состояния (уровня) на другой и когда она находится
в переходном мультимикроцикле. Первый из них является целевым, а второй
обусловлен несовершенством систем и является паразитным, потому что на
его действия отбирается дополнительная энергия, которая была предназначена на
целевые действия.
По определению данному выше, в стационарном состоянии системы функционирует
некоторое определённое число СФЕ, от нуля до всех. Минимальным шагом изменения
уровня функционального состояния является величина, определяемая уровнем
срабатывания одной СФЕ (один квант действия). Следовательно, в принципе, переход
с одного уровня функционального состояния на другой всегда является дискретным
(квантованным), а не гладким, и эта дискретность определяется «калибром» СФЕ.
Число стационарных состояний равно числу СФЕ системы. Системы с большим
количеством «мелких» СФЕ будут проходить через динамические процессы более
гладко и без сильных рывков, чем системы с небольшим количеством «крупных» СФЕ.
Следовательно, динамический процесс характеризуется амплитудой
прироста функций системы от минимума к максимуму (минимакс системы, зависит от
абсолютного числа её СФЕ), дискретностью или шагом прироста функций
(зависит от «калибра» или кванта единичных СФЕ) и параметрами цикличности
функций (скоростью нарастания действий системы, периодом фаз цикла и т.д.). Он
может быть целевым или паразитным.
Следует отметить, что стационарное состояния также является процессом, но
установившимся (стационарным) процессом. В таких случаях состояние систем от
цикла к циклу не меняется. Но во время каждого цикла в системе происходит очень
много различных динамических процессов, потому что система сама состоит из
подсистем, в каждой из которых есть свои циклы и свои процессы. Установившийся
процесс сохраняет систему в одном и том же функциональном состоянии и на одном и
том же стационарном уровне. По определению, данному выше, если система не меняет
своего функционального состояния, то она находится в стационарном состоянии.
Следовательно, установившийся процесс и стационарное состояние – это одно и то
же, потому что независимо от того, находятся ли системы в стационарном состоянии
или в динамическом процессе, в их подсистемах всегда могут быть какие-либо
стационарные или динамические процессы. Например, даже просто рецепция
рецептором «Х» является динамическим процессом.
Отсюда – нет абсолютно инертных (бездеятельных) объектов, любой объект нашего
Мира тем или иным образом как-то действует. Предполагается, что полностью
«бездеятельным» объект может быть при нуле градусов Кельвина (абсолютный нуль).
Попытки получить абсолютно бездеятельные системы предпринимались путём
замораживания тел до долей градусов Кельвина. Но заморозить тело до абсолютного
нуля, видимо, не удастся, потому что тело будет всё равно двигаться в
пространстве, пересекать какие-либо магнитные, гравитационные или электрические
поля и взаимодействовать с ними. Поэтому, вероятно, в принципе невозможно
получить абсолютно инертное и бездеятельное тело.
Целостный организм представляет собой мозаику систем, находящихся или в
разных стационарных состояниях, или в динамических процессах. Можно было бы
возразить, что в организме вообще нет систем в стационарном состоянии, поскольку
в любых его системах постоянно происходят какие-либо динамические процессы. Во
время систолы давление в аорте возрастает, а во время диастолы падает, сердце
постоянно работает, кровь непрерывно течёт по сосудам, и т.д.
Всё это правильно, но оценка функций системы проводится не по текущему её
состоянию, а по циклам её деятельности. Поскольку все процессы в любых системах
циклические, в том числе и в организме, то критерием стационарности является
неизменность интегрального состояния системы от цикла к циклу. Аорта реагирует
на внешнее воздействие (на ударный выброс левого желудочка) тем, что по мере
нарастания давления напряжение её стенок возрастает, и по мере его снижения –
падает. Но если взять период времени больший, чем период одного кардиоцикла, то
интегральное состояние аорты от кардиоцикла к кардиоциклу не меняется и является
стационарным.
3. Оценка функционального состяния систем.
Оценка может быть качественная и количественная. Наличие (отсутствие)
каких-либо волн на кривой является качественной оценкой, а их амплитуда
или частота – количественной. Для оценки функционального состояния любых
систем необходимо сравнение результатов измерений параметров функций с тем, что
должно быть у данной системы. Для того чтобы судить о наличии (отсутствии)
патологии, только измерения какого-либо параметра недостаточно. Например, у
кого-то мы измерили артериальное давление и получили значение 190/100 мм Hg.
Много это, или мало? А сколько должно быть?
Чтобы ответить на эти вопросы нужно сравнить полученный результат с
нормативной шкалой, т.е., с должной величиной. Если полученное значение
отличается от должного, значит есть патология, если не отличается – нет
патологии. Если артериальное давление порядка 190/100 мм Hg наблюдается в покое,
это патология, если на пике максимальной нагрузки, это норма.
Следовательно, должные величины зависят от состояния, в котором находится
данная система. Для оценки параметров существуют нормативные шкалы должных
величин. Существуют максимальные и минимальные должные
величины, должные покоя и пика нагрузки, а также должные кривые
функций.
Минимальные и максимальные должные не всегда должны соответствать состоянию
покоя или пика нагрузки. Например, общее периферическое сосудистое сопротивление
должно быть максимальным в покое и минимальным в нагрузке. Современная медицина
широко использует эти виды должных величин, но почти незнакома с понятием
должных кривых.
Должная величина – это то, что можно наблюдать у большинства нормальных и
здоровых лиц с учётом принадлежности субъекта к определённой нормативной группе
похожих субъектов. Если все имеют такую-то величину и нормально существуют в
данных условиях, то для того, чтобы данный субъект мог также нормально
существовать в этих же условиях, у него должна быть такая же величина. Для этого
используют статистические нормативные шкалы, полученные путём обширных детальных
статистических исследований у определённых групп субъектов. Это так называемые
статистические математические модели. Они показывают, какие параметры
должны быть у данной группы субъектов.
Существуют нормативные таблицы (шкалы) для большинства параметров нормального
и здорового организма человека. Сравнивая данные таблицы с измеренными данными,
полученными при обследовании пациента, можно оценивать их (рис. 16).
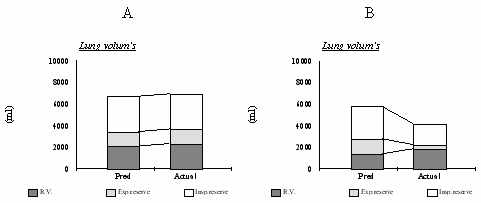
Рис. 16. График с использованием табличных должных. У здорового субъекта
(А) все лёгочные объёмы нормальные. У больного эмфиземой (В) остаточный объём
лёгких увеличен (R.V), а остальные объёмы лёгких уменьшены.
А – здоровый субъект; В – больной эмфиземой лёгких. Pred – табличные
должные величины, Actual – актуальные величины.
Однако использование нормативных таблиц – это примитивный способ оценки
функций систем. Во-первых, они дают должные величины, характеризующие
только группу здоровых лиц, а не данного конкретного субъекта. Во-вторых,
мы уже знаем, что системы каждый момент времени находятся в одном из своих
функциональных состояний и это зависит от внешних воздействий. Например, в покое
система находится на самом низком уровне функционального состояния, а на пике
нагрузке – на самом высоком. Тогда о чём говорят эти таблицы? Вероятно о должных
величинах в состоянии покоя систем организма или на пике их нагрузки. Но ведь
проблемы больных, это не состояние их покоя, и уровень их ежедневной обычной
(рутинной) нагрузки – это не их максимальная нагрузка.
Для нормальной оценки функционального состояния организма больных необходимо
использовать не табличные данные должных величин, а должные кривые
функций систем организма, то, что сегодня почти не применяется. Совпадение или
несовпадение актуальных кривых функций систем организма с должными кривыми будет
мерилом их достаточности или недостаточности. Следовательно, применение
нормативных таблиц является недостаточным и не отвечает требованиям адекватной
диагностики. Применение должных кривых является более информативным (см. ниже).
Статистические математические модели не обладают такой точностью, как бы
точно мы ни измеряли бы параметры. Они показывают, какие величины параметров
должны быть у определённой группы субъектов, похожих по определённым
признакам, например, мужчин в возрасте 20-30 лет, ростом 165-175 см, курящих или
не курящих, женатых или неженатых, белых, желтых или черных и т.д.
Статистические модели намного проще детерминированных, но и менее точные,
поскольку по отношению к данному субъекту можем знать лишь с определённой долей
вероятности, например, в 80%.
Статистические модели применяют в тех случаях, когда мы не знаем всех
элементов системы и законов их взаимодействия. Тогда мы выискиваем похожие
системы по значимым признакам, каким-то образом измеряем результаты действия
всех этих систем, действующих в сходных условиях (клинические испытания), и
вычисляем средний результат действия. Предположив, что данный субъект мало чем
отличается от других, иначе он не был бы похож на них, мы говорим: – «Раз у них
такие-то параметры данной системы в таких-то условиях и они живут без проблем,
значит и у него должны быть такими же эти параметры, если он находится в
этих же условиях».
Однако условия проживания субъекта постоянно меняются. Изменение или неучёт
даже одного значимого параметра может значительно изменить результаты
статистических исследований, и это является большим недостатком статистических
математических моделей. Кроме того, часто статистические модели вообще не
раскрывают суть патологического процесса. Функциональная остаточная ёмкость
лёгких (ФОЕ) показывает объём лёгких в конце нормального выдоха и является
определённым показателем числа функциональных единиц вентиляции ФЕВ.
Следовательно, увеличение ФОЕ указывает на увеличение числа ФЕВ? Но у больных
эмфиземой лёгких ФОЕ значительно увеличена. Что же, у них число ФЕВ увеличено?
Абсурд, поскольку мы знаем, что при эмфиземе происходит разрушение ФЕВ! А у
больных с недостаточностью насосной функции левого желудочка наблюдается
уменьшение ФОЕ. Значит у них уменьшено число ФЕВ? Без знания динамики функций
аппарата внешнего дыхания и лёгочного кровообращения невозможно дать точного
ответа на эти вопросы.
Следовательно, основной недостаток статистических моделей заключается в том,
что достаточно достоверные результаты исследований можно получить лишь в том
случае, если строго соблюдать все значимые условия, которые определяют данную
группу субъектов. Изменение или добавление одного или нескольких значимых
условий исследования, например, рост, пол, вес, цвет глаз, открытое окно во
время сна, место жительства и т.д., может сильно изменить конечный результат,
добавив новую группу субъектов. В результате, если мы хотим знать, например,
жизненную ёмкость лёгких у жителей Нью Йорка, мы обязаны проводить исследования
именно у жителей Нью Йорка, а не у жителей Москвы, Парижа или Пекина, и эти
данные могут не подходить, например, для жителей Рио де Жанейро. Более того,
нормативы у жителей разных районов Нью Йорка могут быть различными, в
зависимости от национальной принадлежности, загрязнённости внешней среды этих
районов, социального уровня и пр.
Конечно же можно исследовать все мыслимые варианты групп субъектов и
выработать нормативы, например, для мужчин в возрасте от ... и до..., курящих
или не курящих сигары (трубки, сигареты или папиросы) с высокой (низкой)
концентрацией никотина, коренных жителей (эмигрантов), белых, чёрных или желтых
и т.д. Это потребует гигантских усилий и всё равно не оправдает себя, поскольку
мир постоянно меняется и эту работу каждый раз придётся повторять. Тем более
невозможно выработать статистические нормативы для бесконечного числа групп
субъектов во время динамических процессов, например, физических нагрузок, в
разные фазы патологических процессов и т.д., когда число значений каждого
отдельного параметра очень велико.
В результате появляется эмпирическая модель в виде формулы (В). Эта модель
более точная, чем статистическая, но она всё ещё носит вероятностный характер.
Когда известны все детали системы и полностью раскрывается механизм её работы,
появляется детерминированная математическая модель в виде формулы (С). Её
точность обусловлена только точностью методов измерения.
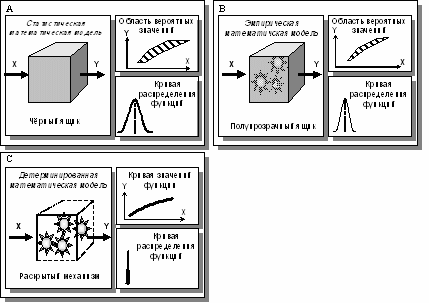
Рис. 17. Виды математических моделей систем на примере «чёрного ящика».
Когда совершенно неизвестны детали системы, но известны варианты реакции
системы и их весовые вероятностные коэффициенты, появляется статисти-ческая
математическая модель системы (А). Неточность этих моделей носит принципиальный
характер и обусловлена вероятностным характером функций. По мере изучения
системы начинают проявляться детали её строения.
В результате появляется эмпирическая модель в виде формулы (В). Эта модель
более точная, чем статистическая, но она всё ещё носит вероятностный характер.
Когда известны все детали системы и полностью раскрывается механизм её работы,
появляется детерминированная математическая модель в виде формулы (С). Её
точность обусловлена только точностью методов измерения.
Применение статистических математических моделей оправдано на первых этапах
любого познания, когда детали изучаемого явления неизвестны. На этом этапе
познания вводится понятие «чёрного ящика», когда мы ничего не знаем о строении
этого «ящика», но нам известна его реакция на некоторые воздействия (рис. 17).
Типы его реакций выявляются с помощью статистических моделей и далее, с помощью
логики, выявляются детали его систем и их взаимодействие. Когда всё это
выявлено, наступает очередь детерминированных моделей, а оценку функций систем
проводят не по табличным данным, а по должной кривой функции системы.
Должная кривая функции систем организма – это должное множество
значений функции данной конкретной системы у данного конкретного субъекта при
изменении её нагрузки от минимума до максимума. Сегодня должные кривые почти не
используются и вместо должных кривых применяют экстремальные минимальные и
максимальные должные величины. Например, должная вентиляуия лёгких в покое и на
пике нагрузки. Для этого проводят максимальную нагрузку в однотипных группах
людей и измеряют вентиляцию лёгких в покое и на пике нагрузки. После
статистической обработки появляются должные величины вентиляции лёгких для
условий покоя и пика нагрузки. Недостаток экстремальных должных величин
заключается в том, что этот метод мало пригоден для больных. Не все больные
могут нормально выполнить нагрузку и прерывают её задолго до достижения должного
максимума. Больной мог, например, дать должную вентиляцию лёгких, но он просто
прекратил нагрузку слишком рано. Как же оценивать функцию? Это можно сделать
только с помощью должной кривой. Если актуальная кривая совпадает с должной
кривой, функция нормальная на участке совпадения. Если актуальная кривая ниже
должной кривой, она отстающая (рис. ).
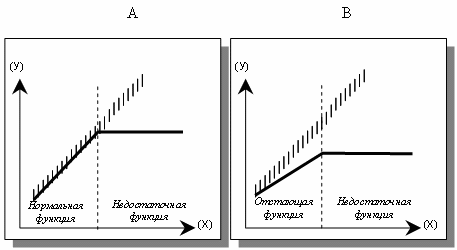
Рис. 33. Нормальная (А) и отстающая функци (В).
Наклонная прямая из вертикальных отрезков прямой – должная кривая.
Вертикальная пунктирная прямая – граница перехода нормальной или отстающей
функции в недостаточную (в плато)
Недостаток должных кривых в том, что для их построения необходимо
использовать детерминированные математические модели систем, которых пока
есть очень мало. Они строятся на основе знания причинно-следственных связей
между элементами системы. Эти модели наиболее сложные, трудоёмкие и во многих
случаях пока невыполнимые. Поэтому в практической медицине они почти не
применяются и это является причиной остутствия аналитической медицины. Но они
наиболее точные и показывают, какие параметры должны быть у данного
конкретного субъекта в любой момент времени. Только использование должных
кривых функций позволяет верно оценить актуальные кривые (рис. 18).
Отличие детерминированных математических моделей от статистических таблиц
заключается в том, что в первом случае вырабатываются должные величины для
конкретно данного субъекта (персональные должные), а во втором – должные
величины для группы похожих на данного субъекта лиц. Возможность
построения детерминированных моделей зависит только от меры нашего знания об
исполнительных элементах системы и законов их взаимодействия.
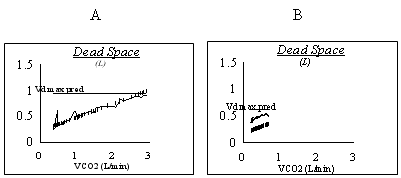
Рис. 18. Графики с использованием должных кривых. Актуальные кривые
в виде черных кривых, должные кривые в виде наклонных прямых из серии
вертикальных льоезков прямых. У здорового (А) субъекта актуальная кривая
суммарного объема бронхов (dead space), измеренная во время теста с максимальной
физической нагрузкой, совпадает с вычисленной должной кривой и доходит до
табличной максимальной должной (Vd max pred). У больного эмфиземой (В)
актуальная кривая выше должной, но не доходит до максимальной должной. Если бы
этот параметр оценивали по табличной максимальной должной величине, то у
больного оценка параметра была бы снижена, хотя расположение актуальной кривой
выше должной кривой показывает, что этот параметр у него увеличен. Просто он не
выполнил нагрузку в том объеме, в котором должен был выполнить (его VCO2
было намного меньше, чем у здорового).
Примером детерминированной математической модели в медицине и биологии
теплокровных животных является определение ударного выброса левого желудочка по
формуле Фика [12]:
| |
VO2 = CO * {1.34 * Hb * [(SaO2a
– SaO2v) : 100]} |
(Л/мин) |
(32) |
| где: |
CO - |
сердечный выброс левого желудочка (Cardiac Output) |
(Л/мин) |
| |
1.43 - |
коэффициент Huffner, показывает, сколько мл О2
может вместить в себя 1 г гемоглобина при 100% насыщения |
(мл/г) |
| |
VO2 - |
потребление кислорода в единицу времени |
(Л/мин) |
| |
Hb - |
количество гемоглобина в 1 литре крови |
(г/Л) |
| |
SaO2a - |
насыщение артериальной крови кислородом |
(%) |
| |
SaO2v - |
насыщение венозной крови кислородом |
(%) |
Мы знаем, что 1 гр гемоглобина максимально может вместить 1.34 мл О2
[16]. Мы можем измерить насыщение кислородом в крови, вытекающей из лёгких и из
тканей. Зная артерио-венозную разницу по насыщению, количество гемоглобина в
крови, величину потреблённого кислорода в единицу времени и частоту пульса, мы
можем получить, например, величину ударного выброса в 56 мл. При этом можем быть
уверены, что он именно такой, ни больше и не меньше, при условии, что мы точно
измерили все необходимые для расчётов параметры.
Примером статистической нормативной шкалы в механике может быть вычисление
вероятности попадания очередного броска камня в заданную цель. После серии
бросков, выполнив определённые статистические вычисления можно прогнозировать,
что очередной бросок с такой-то степенью вероятности попадёт в цель.
Если же для этого использовать детерминированную математическую модель
(баллистику), то зная вес камня, силу и угол броска, вязкость воздуха, скорость
и направление ветра и т.д., можно точно вычислить и предсказать место падения
камня. «Дайте мне точку опоры и я переверну земной шар», скал Архимед, имея
ввиду, что у него была детерминированная математическая модель механики
движений.
Живой организм – слишком сложная и многокомпонентная система. Учесть все
параметры и их взаимосвязи невозможно, поэтому статистические математические
модели не могут адекватно описать состояние систем организма. Но совместное
использование статистических и детерминированных моделей позволяет с достаточной
степенью точности оценивать параметры живых систем.
Со временем, по мере накопления знаний, статистические модели сменяются
детерминированными. Техника намного проще биологии и медицины, потому что
объектом её познания являются относительно простые системы (машины), построенные
человеком. Поэтому её развитие и процесс смены статистических математических
моделей на детерминированные ушёл далеко вперёд, по сравнению с медициной. Тем
не менее, на передовых позициях любых наук, в том числе и технических, там, где
не всё ещё ясно и познано, статистика сохраняет свои позиции, поскольку она
помогает выявлять элементы систем и законы их взаимодействия.
Медицина намного сложнее техники. Объектом её познания является живой
организм, тоже машина, но более сложная. И в медицине сохраняется тот же процесс
познания, что и в технике. Особенности этого процесса в медицине касаются только
сложности изучаемых объектов и этических проблем. В остальном – это схожие
процессы. Если бы мы знали все физические параметры элементов систем организма и
могли бы описать термодинамику всех химических процессов в нём, мы смогли бы
построить свою теорию медицины, подобную физическим или техническим теориям. В
этом случае, используя детерминированные математические модели мы смогли бы
описать, а значит оценить и предсказать поведение любых систем организма с
заданной точностью, которая пока достижима только в технике или механике. Но
построение детерминированных математических моделей в медицине, в силу
чрезвычайной сложности изучаемых объектов – это пока очень трудно разрешимая
проблема. Тем не менее, появление таких моделей в медицине не только насущная
потребность, но реализуемый, хотя и медленно, процесс.
Если взять шкалу от 0 до 100%, где за 0 принять уровень табличных
статистических значений, а за 100% – уровень полностью детерминированных
математических моделей, то все имеющиеся в нашем распоряжении эмпирические
математические модели будут где-то между 0 и 100%.
Применение детерминированных моделей значительно упрощает понимание
процессов, происходящих в живом организме. Все мы построены примерно из одних и
тех же материалов – белков, жиров, углеводов, минералов и воды. Ткани тела
негров, китайцев, индейцев, папуасов, примерно такие же, как и у русских,
англичан или немцев. Их развитие (раскрытие функциональных резервов) может быть
на разных уровнях, в зависимости от условий проживания, но тела любых людей
построены из одних и тех же СФЕ. Зная все параметры каждого типа СФЕ организма
человека, можно подсчитать, сколько таких-то единиц необходимо для выполнения
таких-то функций. Если одна лёгочная функциональная единица (ЛФЕ) может
пропустить через себя, скажем, 0,0001 мл О2 в минуту (цифры
произвольные), то для обеспечения 2 000 мл/мин нам потребуется около 20 000 000 ЛФЕ.
Если организм располагает таким числом ЛФЕ, то всё в порядке. Если их не
хватает, то нагрузка, требующая 2 000 мл/мин О2 уже будет
перегрузкой, со всеми вытекающими отсюда последствиями.
Далее, для чего мы проводим обследование субъекта и оценку функций систем его
организма? Для того, чтобы знать, насколько он отличается от ему подобных?
Возможно. Но, вероятно, основная цель обследования больного – определить, может
ли он нормально существовать без медицинской помощи и если нет, то какую помощь
ему оказать. Патологический процесс – это процесс разрушения каких-либо СФЕ
систем организма, в котором одну из ключевых ролей играет порочный круг. Однако
порочные круги начинают срабатывать лишь при определённой степени нагрузки. Ниже
этого уровня они не появляются и не разрушают СФЕ. Т.е., ниже определённого
порога нагрузки (механической, тепловой, токсической и т.д.) нет патологического
процесса, и нет болезни.
Следовательно, определив порог начала появления порочного круга, мы сможем
узнать верхний «потолок» качества жизни данного больного. Если условия его
проживания (ритм жизни) позволяют ему не превышать этот «потолок», значит в этих
условиях данный субъект не будет болеть. Если ритм жизни требует больше, чем
могут дать возможности его организма, то он будет болеть. Чтобы не болеть он
должен ограничить себя в некоторых своих действиях. Ограничить себя в своих
действиях – это значит снизить уровень жизни, лишить себя возможности выполнять
некоторые действия, которые могут делать другие, или которые он сам делал ранее,
но которые сейчас недоступны данному больному в силу ограничения ресурсов его
организма из-за дефектов.
Если эти ограничения касаются только получения удовольствий, таких как,
например, игра в футбол, это как-то можно перенести. Но если эти ограничения
касаются условий жизни больного, то нужно каким-то образом это учесть. Например,
если его квартира расположена на первом этаже, то для вполне нормального образа
жизни его максимум потребления О2 должен быть, например, 1 000 мл в
минуту. Но если он проживает, например, на третьем этаже, а в доме нет лифта и
для подъёма на третий этаж пешком он должен уметь усваивать 2 000 мл/мин О2,
в то время как он может усваивать всего лишь 1 000 мл/мин О2, то что
же делать? У больного возникает проблема, которую можно решить лишь с помощью
каких-либо лечебных мероприятий или сменив условия жизни.
В клинической практике мы почти не оцениваем функциональное состояние
больного с точки зрения его соответствия условиям проживания. Конечно это
тривиально и мы догадываемся об этом, но пока ещё нет объективных критериев и
соответствующей методологии оценки соответствия функциональных резервов
организма больного условиям его жизнедеятельности. Эргономика невозможна без
системного анализа.
Основным критерием достаточности функций организма для данных условий его
проживания должно быть отсутствие возникновения порочных кругов (см. ниже) при
данном уровне обычных жизненных нагрузок. Если в данных условиях возникают
порочные круги, то нужно либо каким-то образом усилить функции систем организма,
либо данный больной обязан сменить условия проживания, чтобы порочные круги не
срабатывали, либо он будет постоянно болеть со всеми вытекающими отсюда
последствиями.
Таким образом, мы нуждаемся не только в знании минимальных или
максимальных должных величин, которые мы можем получить используя
статистические математические модели. Мы также нуждаемся в знании бытовых
должных величин этих же параметров, которые должны быть у данного
конкретного больного, чтобы условия его проживания не приводили бы к развитию
патологических процессов и не разрушали бы его организм. А для этого нам нужны
детерминированные математические модели.
Системы стабилизации и пропорциональные системы.
Существует множество типов различных систем. Но для нас особое значение имеют
системы стабилизации и пропорциональные системы. У первых
результат действия всегда сохраняется один и тот же (стабильный), не зависит от
силы внешнего воздействия, но зависит от уставки. Например, рН крови должен быть
всегда равен 7.4, артериальное давление – 120/80 мм Hg, и т.д. (системы
гомеостаза), независимо от внешних воздействий.
У вторых результат действия зависит от силы внешнего воздействия по
какому-либо определённому закону, задаваемому уставкой, и пропорционален ему.
Например, чем больше мы выполняем физической работы, тем больше мы должны
потреблять О2 и выделять СО2.
Система стабилизации использует два рецептора – «Х» и «Y». Рецептор «X»
используется для запуска системы в зависимости от наличия внешнего воздействия,
а рецептор «Y» – для измерения результата действия. На вход уставки блока
управления системы стабилизации подается уставка – задание, какой величины
должен быть результат действия. Система стабилизации должна выполнять это
задание, т.е., поддерживать (стабилизировать) результат действия на заданном
уровне, независимо от силы внешнего воздействия.
Стабильность результата действия обеспечивается тем, что в «базе данных»
блока управления есть соотношения числа активных СФЕ и силы внешнего воздействия
и осуществляется по логике ООС – если результат действия увеличился, то нужно
уменьшить его, если уменьшился, то увеличить его. Для этого блок управления
должен содержать ППС и ООС. Следовательно, простейший блок управления (ППС) для
систем стабилизации не подходит. Нужен как минимум простой блок управления,
который содержит также и ООС.
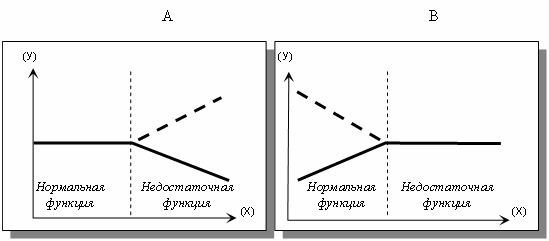
Рис. 19. Функции системы стабилизации (А) и пропорциональной системы (В).
У системы стабилизации до вертикальной пунктирной прямой результат
действия системы стабильный (нормальная функция, кривая идёт горизонтально).
После пунктирной прямой функция падает (возрастает), - стабилизация нарушилась
(недостаточность функции). У пропорциональной системы до вертикальной пунктирной
прямой её функция нарастает (падает) пропорционально внешнему воздействию
(нормальная функция). После пунктирной прямой функция не меняется (вошла в
насыщение, перешла в плато - недостаточная функция).
В системе стабилизации измерительный элемент постоянно измеряет результат
действия системы и передаёт его в блок управления, который сравнивает его с
заданным. В случае расхождения результата действия с заданием этот блок
принимает решение о тех или иных действиях и заставляет элементы исполнения
действовать таким образом, чтобы это расхождение исчезло.
Внешнее воздействие может меняться в различных пределах, но результат
действия должен оставаться стабильным и быть равным заданному. На это система
затрачивает свои ресурсы. Если ресурсы заканчиваются, система стабилизации
перестаёт стабилизировать результат действия и с этого момента начинается её
недостаточность (рис. 19А, 21А).
Примером стабилизации, например, является скорость вращения звезды в вакуме.
Если радиус звезды уменьшится, то скорость её вращения увеличится и усилятся
центробежные силы, которые увеличат её радиус и скорость вращения уменьшиться.
Если радиус звезды увеличится, то всё произойдёт в обратном порядке. На этом же
принципе фигурист на льду регулирует скорость вращения своих пируэтов.
Система стабилизации артериального давления также является примером систем
стабилизации (ССАД). Её задача – поддерживать артериальное давление на заданном
уровне, независимо от уровня физической нагрузки и внешних условий. Но мы видим
повышение АД на пике нагрузки! Может быть ССАД не является системой
стабилизации?
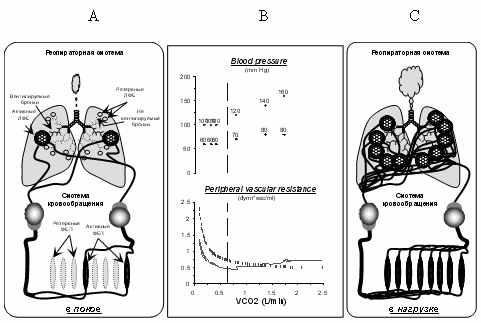
Рис. 20. Система кровообращения в покое (А) и в нагрузке (С)..
В покое работает только часть ФЕП, а в нагрузке - все. Пока были резервы
ФЕП, ОПСС (peripheral vascular resistance) снижалось (нижний график на «B»),
хотя сердечный выброс продолжал нарастать (увеличение VCO2). Поэтому
АД не менялось Как только все ФЕП были задействованы, кривая ОПСС перешла в
плато и возник порог анаэробного обмена (ПАО – вертикальная пунктирная линия) и
АД стало возрастать.
Нет, ССАД является системой стабилизации, потому что во время выполнения
физических нагрузок АД практически не менятся вплоть до появления порога
анаэробного обмена (ПАО на графиках на рис. 20B, до вертикальной пунктирной
прямой). По мере нарастания нагрузки увеличивается число включаемых в
кровообращение сосудистых микроциркуляторных сегментов – функциональных единиц
перфузии (ФЕП), и общее периферическое сосудистое сопротивление (ОПСС) падает.
ФЕП являются системными функциональными единицами ССАД. В какой-то момент резерв
этих ФЕП заканчивается и ОПСС перестаёт падать, хотя нагрузка продолжает
увеличиваться. С этого момента начинается недостаточность ССАД и появляется ПАО.
Пока было падение ОПСС, левому желудочку сердца было легко наращивать
сердечный выброс и увеличивать кровоснабжение тканей. Но как только резерв ФЕП
заканчивается, ОПСС перестаёт падать, но левый желудочек продолжает наращивать
свои насосные функции, сердечный выброс нарастает. Поэтому с этого момента АД
начинает возрастать. Но с этого момента левому желудочку уже не так легко
проталкивать всё большие объёмы крови через неменяющийся суммарный диаметр
микрососудов. Возникает отставание насосных функций сердца от ожидаемых (от
должных, целевых) и из-за недостатка снабжения тканей кислородом в крови
появляется молочная кислота, которая является признаком недостаточности
кислородного снабжения (анаэробных процессов) в тканях. Следовательно, подъём
систолического и среднего артериального давления после появления ПАО происходит
не потому, что так должно быть, а потому, что ССАД имеет ограниченные
биологические ресурсы.
Примерами систем стабилизации являются также все системы гомеостаза организма
(газы крови, электролиты крови – К+, Na+, система стабилизации температуры и
др.).
Пропорциональная система также должна использовать оба рецептора «Х» и «Y».
Один из них измеряет входное воздействие а другой – результат действия системы.
На вход блока управления подается уставка – задание, какой должна быть
пропорция между внешним воздействием и результатом действия. Поэтому такие
системы называются пропорциональными. Внешнее воздействие может меняться в
различных пределах. Но блок управления должен подстраивать работу элементов
исполнения таким образом, чтобы сохранялась та пропорция между внешним
воздействием и результатом действия, которая была «предписана» (задана) в
уставке.
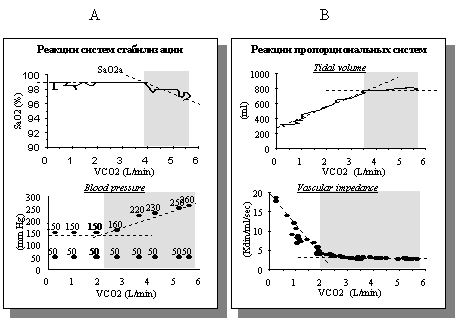
Рис. 21. Примеры реакций систем стабилизации (А) и пропорциональных систем
(В) .
Кривые были получены во время масимальной физической нагрузки у
спортсмена. На оси Х отложена величина минутного выделения СО2 (VCO2), которая
нарастала пропорционально росту нагрузки. Чётко видны точки перегиба кривых.
Точки перегиба во всех случаях означают начало недостаточности функции. Серым
фоном обозначены зоны недостаточности функций. На обоих нижних графиках зоны
недостаточности функций совпадают с ПАО. Артериальное давление (blood pressure)
до ПАО не меняется.
Если пропорция сохраняется, на графике функции будет отмечаться нарастание
(падение) кривой (нормальная функция, рис. 19B, 21B) Но если ресурсы системы
исчерпаны, она не сможет сохранять необходимую пропорцию между внешним
воздействием и результатом действия. С этого момента она не сможет наращивать
(снижать) свои функции пропорционально входному внешнему воздействию и кривая её
функции перейдёт в плато (недостаточная функция, рис. 19B, 21В).
Примерами пропорциональных систем являются, например, усилители электрических
сигналов, механические рычаги, морские течения (чем больше прогрев воды в
океане, тем сильнее Гольфстрим), атмосферные явления и т.д.
Примерами такого рода систем могут быть сами сенсоры, поскольку величина их
результата действия (частота импульсации, амплитуда напряжения, и т.д.)
пропорциональна внешнему воздействию.
Система обмена метаболических газов (СОМГ), система внешнего газообмена (СВГ)
и система кровообращения (СК) являются примерами пропорциональных биологических
систем нашего организма. В ответ на увеличение физической нагрузки они
наращивают свои функции.
Таким образом, примеры систем стабилизации и пропорциональных системы можно
найти в любом мире, и не только в биологических системах.
Активные и пассивные системы.
Пассивными системами называются те системы, которые не затрачивают
энергии на свои действия.
Активными системами называются те системы, которые затрачивают энергию на
свои действия.
Однако, как уже не раз подчёркивалось, любое действие любых систем требует
затрат энерги. Ни одно действие, даже самое ничтожное, невозможно без затрат
энергии, потому что, как уже было сказано, действие – это всегда взаимодействие
между системами или её элементами. А любое взаимодействие – это связь между
системами или её элементами, которая для своего создания требует вложения в неё
энергии. Поэтому любое действие требует затрат энергии. Следовательно, любые
системы потребляют энергию, в том числе и пассивные. Различие между активными и
пассивными системами только в источнике энергии. Каким же образом действует
пассивная система?
Если система находится в равновесном состоянии с окружающей средой и на неё
не оказывается никакого воздействия, то система не должна делать никаких
действий. А раз она не совершает действий, она не потребляет энергию. Она
пассивна до того момента, когда она начнёт действовать и лишь тогда начнёт
потреблять энергию.
На рис. 22А равновесие карандаша обусловлено сбалансированным толканием
(давлением) пружин на карандаш. Пружинки являются не просто случайными группами
элементов (набором атомов и молекул), а пассивными системами с петлями
ООС и исполнительными элементами на молекулярном уровне (межмолекулярными силами
в стальных пружинках), которые стремятся сбалансировать силы межмолекулярных
связей, что проявляется в виде силы напряжения пружин. Поскольку в случае
отсутствия внешнего воздействия нет действий самой системы, то нет и энерготрат
(рис. 22А), система пассивно ждёт появления внешнего воздействия.
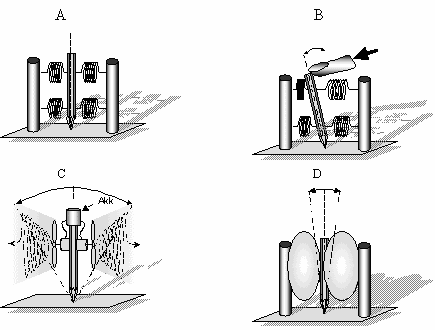
Рис. 22. Пассивная (А, В, D) и активная системы (С).
У обоих типов систем одна и та же цель – удерживать карандаш в
вертикальном положении. В пассивной системах эта функция выполняется пружинами
(пассивными СФЕ, А и В) и столбами воздуха, заключёнными в резиновые баллончики
(пассивные СФЕ, D). СФЕ запасают (используют) энергию во время внешнего
воздействия (толкание пальцем карандаша сдвавливает пружинки). В активной
системе (С) эта же функция достигается за счёт струй воздуха, которые постоянно
разрушаются. Эти струи создают моторные вентиляторы (активные СФЕ), которые
затрачивают энергию, ранее запасённую, например, в аккумуляторах (на рисунке -
Акк). Если заключить воздух этих струй в резиновые баллоны, то они уже не
разрушатся и будут существовать независимо от вентиляторов, выполняя ту же
функцию. Но это уже пассивная система (D).
Но вот внешнее воздействие появилось и карандаш отклонился в сторону (рис.
22В). Пружины тут же стремятся вернуть карандаш в прежнее положение, т.е.,
система начинает действовать. Откуда она берёт энергию для своих действий? Эту
энергию принесло внешнее воздействие в виде кинетической энергии толкания
пальцем, которое сжало (растянуло) пружинки и они запасли эту энергию в виде
потенциальной энергии сжатия (растяжения). Как только внешнее воздействие
(толкание пальцем) прекратилось, потенциальная энергия сжатых пружин
превращается в кинетическую энергию их распрямления и это возвращает карандаш
обратно в вертикальное сбалансированное положение.
Внешнее воздействие повышает внутреннюю энергию системы, которая затем
используется для деятельности системы. Есть воздействие – есть избыток
внутренней энергии системы, есть ответное действие системы. Нет воздействия –
нет избытка внутренней энергии системы, нет её действия. Внешнее воздействие
приносит энергию в систему, которая использует её для реакции на это
воздействие.
Функции пружин могут выполнять струи воздуха, создаваемых вентиляторами,
расположенными на карандаше (рис. 22С). На «постройку» струй воздуха
затрачивается избыток энергии системы «вентиляторы-карандаш», также привнесённой
извне но сохраняемой до нужного времени (например, бензин в баке или
электричество в аккумуляторе). Такая система уже будет активной, потому
что использует свою внутреннюю энергию, а не энергию внешнего воздействия.
Отличие струй воздуха от пружин состоит в том, что струи воздуха состоят из
случайных групп молекул воздуха (не системы), движущихся в одном направлении.
Среди этих элементов есть элементы исполнения (СФЕ – молекулы воздуха), но нет
блока управления, который мог бы построить систему из них наподобие пружин,
т.е., обеспечить существование струй воздуха как стабильных отдельных и
независимых тел (систем). Эти струи воздуха постоянно строятся пропеллерами
вентиляторов и, поскольку у них нет собственного блока управления, постоянно
сами собой разрушаются. Если построить какую-либо систему, которая позволит
струям воздуха не разрушаться, например, заключить их в резиновые баллоны (рис.
22D), то они смогут существовать уже независимо от вентиляторов. Но в этом
случае система стабилизации вертикального положения карандаша перейдёт из
категории активных в пассивную.
Следовательно, как активные, так и пассивные системы потребляют энергию.
Однако пассивные потребляют внешнюю энергию, привносимую самим внешним
воздействием, а активные – свою собственную внутреннюю энергию.
Могут возразить, что внутренняя энергия, скажем, миоцита всё равно является
внешней, привнесённой в клетку извне, например, в виде глюкозы. Это правда, и
более того, любой объект содержит внутреннюю энергию, которая когда-либо была
внешней. И, возможно, мы даже знаем источник этой энергии – это энергия Большого
Взрыва. На создание любого атома когда-то и где-то была затрачена определённая
энергия, которую тем или иным путём можно извлечь из него. Такая внедрённая
внутренняя энергия есть у любого объекта нашего Мира и невозможно найти никакой
другой объект в нём, который бы содержал абсолютно свою собственную внутреннюю
энергию, которую ничто и никогда не внедряло в него. Всегда при взаимодействии
систем происходит обмен энергией. Но во время своей деятельности пассивные
системы не тратят свою внутренню энергию, потому что не «умеют» этого делать, а
используют только энергию внешнего воздействия. А активные системы могут тратить
свою внутреннюю энергию.
Примерами активных систем в биологии являются миоциты, нейроны, секреторные
клетки и все прочие системы, потребляющие в качестве энергии АТФ, который в
нужный момент образуется в анаэробных и аэробных процессах из заранее запасёной
глюкозы (гликогена).
Примерами пассивных систем являются аорта и вообще все артериальные
сосудистые сети БКК и МКК, запасающие энергию ударного выброса во время систолы
желудочков путём растяжения их упруго-эластических стенок. Во время диастолы эта
запасённая потенциальная энергия растянутых артериальных стенок расходуется на
их сокращение и выталкивание крови из артериальной сети в капиллярную и далее.
Пассивной системой является также грудная клетка, которая осуществляет
пассивный выдох, и многие другие системы живого организма.

