Гл. 1. Проблема познания истины

1.1. Понятие материальной реальности

Назовем материальной реальностью все то, что возникает и исчезает и, следовательно, имеет время возникновения t₁ и время исчезновения t₂:

- ∞ < t₁ < t₂ < + ∞

Ясно, что если что-то возникает и исчезает, то в течение времени от момента возникновения t₁ до момента исчезновения t₂ оно существует объективно, т.е. независимо от воли человека.

Следовательно, выше введенное понятие материальной реальности (МР) не находится в противоречии с понятием материальной реальности, издавна используемым в философии. Тем не менее, эти два понятия отличаются друг от друга. Это отличие проявляется при выяснении вопроса: является ли Мироздание материальной реальностью?

В самом деле, по выше приведенному определению МР, Мироздание является материальной реальностью, если у него имеются время возникновения и время исчезновения. В противном случае, Мироздание материальной реальностью не является. Вместе с тем, по понятию материальной реальности, используемому в современной философии, Мироздание является материальной реальностью без всяких оговорок. Ведь, оно объективно существует!

Как видно, выше приведенное понятие МР чуть уже и, следовательно, определеннее, чем понятие МР, используемое в современной философии.

В медицине и биологии вместо словосочетания «Материальная реальность», используют словосочетания «Живой организм», а в физике говорят о физическом теле.

1.2. Множество, пара и элементы пары

Понятие «Множество», как известно, является первичным математическим понятием. Если множество бинарное, то говорят, что оно является отношением.

Пусть, A - непустое конечное множество материальных реальностей, а H является конечным множеством отношений, заданным на множестве A.

Пусть, S материальная реальность такая, что выполняются следующие условия.

1.Имеют место

S = A при H = Æ и S ¹ A при H ¹ Æ

2. Справедлива зависимость

a_j Î A Û a_j Î S для всех j = 1..n,

где

n - количество элементов множества A.

Тогда и только тогда говорят, что МР S является парой множеств A и H и пишут:

S = <A,H>

Об элементах множества А, т.е. о материальных реальностях

a_j; j = 1..n

говорят, что они одновременно являются и элементами пары S.

1.3. Естественные измерительные приборы

У человека, страдающего ишемической болезнью сердца (ИБС), часто немеют конечности. Это, как правило, вызвано нехваткой кислорода. Вместе с тем головной мозг этого человека продолжает получать кислород исправно в нужном объеме.

В итоге, в одних частях организма больного ИБС устанавливаются одни значения концентрации кислорода, а в других частях – другие.

Так происходит не только в организме больного ИБС и не только с концентрацией кислорода, а в любом живом организме и с любой величиной, служащей характеристикой состояния этого организма. Надо полагать, что вообще так происходит в любой материальной реальности. А это, по сути дела, означает признание того, что каждая МР имеет свой собственный «парк средств измерения». В случае кислорода, в частности, в качестве измерительных приборов выступают клетки живого организма. Ведь, без кислорода клетки существовать не могут!

В случае артериального давления в роли измерительных приборов выступают соответствующие участки артерии. Аналогично, о венозном давлении головной мозг судит по наполнению соответствующих участков вен и т.д.

Вообще под измерительными приборами МР понимают следующее.

Пусть

a Î S и b Î S

- материальные реальности, а

y_a и y_b

являются скалярными величинами, такими, что выполняются следующие условия.

1. Величины y_a и y_b устанавливаются путем измерения, т.е. они являются количественно измеряемыми величинами.

2. Эти величины имеют одинаковые размерности и измеряются в одних и тех же единицах измерения.

3. Имеет место

y_a ≥ 0 при y_b £ 0 или y_a £ 0 при y_b ≥ 0,

т.е. во всех случаях, когда имеет место y_a ¹ 0 и y_b ¹ 0, эти величины имеют противоположные знаки.

Определение 1.1.

Говорят, что материальные реальности a Î S и b Î S в течение времени от t₁^* до t₂^* (t_{1 £} t₁^* < t₂^*£ t₂) служат партнерами, если выполняются следующие условия.

1. Вполне определенные изменения МР a Î S приводят к соответствующим, тоже вполне определенным, предсказуемым изменениям МР b Î S. И, наоборот, вполне определенные изменения МР b Î S приводят к соответствующим, тоже вполне определенным, предсказуемым изменениям a Î S.

2. Имеет место

│y_a + y_b│ ≤ 0,

В определении 1 особо следует обратить внимание на предсказуемость результата. Системы с непредсказуемыми, случайными результатами не могут служить в качестве партнеров [5].

Партнерами являются, например, любые два участка ткани живого организма, между которыми происходят обмен веществ. Партнерами являются особы противоположных полов одного и того же биологического вида, составляющие семью и т.д.

Определение 1.2

Пусть, материальные реальности a Î S и b Î S служат партнерами и при этом в момент времени t = t₀ (t₁^* £ t₀ £ t₂^*) имеет место:

│y_a + y_b│ = 0

Тогда и только тогда говорят, что материальные реальности a Î S и b Î S в момент времени t = t₀ служат идеальными партнерами.

Если материальные реальности a Î S и b Î S служат идеальными партнерами в течение всего времени от t₁^* до t₂^*, то говорят, что они составляют идеальную пару.

Примерами идеальных пар служат «Орел + решка», «Электрон + позитрон», «Фотон + антифотон» и т.д.

Участки ткани живого организма, между которыми происходит обмен веществ, в момент времени t = t₀ могут служить в качестве идеальных партнеров, а могут и не служить. Если они при t = t₀ служат идеальными партнерами, то от них в высшие органы управления живого организма не поступает никакой информации. В этом случае высшим органам управления нет необходимости вмешиваться во «внутренние дела» пары. Необходимость вмешательства возникает только в том случае, когда

ç y_aç > ç y_bç > 0 или 0 < ç y_aç < ç y_bç

Тогда и возникает проблема измерения величин y_a и y_b со стороны высшего органа управления живого организма. Измерение этих величин требуется для того, чтобы была установлена и устранена причина возникшего дисбаланса. Надо полагать, что так происходит не только в живом организме, а в любой материальной реальности. Отсюда смысл следующего положения.

Определение 1.3.

Пусть, материальные реальности a Î S и b Î S в течение времени от t₁^* до t₂^* служат партнерами.

Тогда и только тогда говорят, что МР a Î S в течение времени от t₁^* до t₂^* является естественным измерительным прибором величины y_b, а МР b Î S является естественным измерительным прибором величины y_a.

В социологии словосочетание «Естественный измерительный прибор» обозначают одним словом: «Потребитель». А вообще будет лучше, если скажем: «Пользователь».

Ясно, что материальная реальность a Î S будет пользователем МР b Î S, а материальная реальность b Î S – материальной реальности a Î S.

1.4. Первичные показатели качества функционирования МР

Пусть, материальные реальности a Î S и b Î S такие, что

a = a_i и b = b_j; i = i₀; j = j₀; i₀,j₀ = 1..n; i₀ ¹ j₀

и, следовательно, имеет место

a_i Î S и b_j Î S; i = i₀; j = j₀; i₀,j₀ = 1..n; i₀ ¹ j₀,

где

n – количество элементов пары S.

Определение 1 4

Пусть, для любых МР a_i Î S и b_j Î S существуют величины

y_i и y_j; i = i₀; j = j₀; i₀, j₀ = 1..n; i₀ ¹ j₀

такие, что имеют место

y_i = ç y_aç и y_j = ç y_bç ; i = i₀; j = j₀; i₀,j₀ = 1..n; i₀ ¹ j₀

Тогда и только тогда говорят, что величины

y_j; j = 1..n

являются первичными показателями качества функционирования МР S.

Как видно

y_j ≥ 0; j = 1..n

В медицине и биологии вместо термина «Первичный показатель качества функционирования МР S» используют словосочетание: « Первичный показатель состояния здоровья».

1.5. Истина и вероятностный предел ее познания

Пусть

Y = {y_j; j = 1..n} (1.1)

- генеральная совокупность первичных показателей качества функционирования МР S, а

B_j = {b_jl ; l = 1..N_j}; j = 1..n

- выборки результатов измерений у МР S показателей

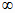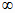0 < y_j < ; j = 1..n; n < (1.2)

Положим, что каждая выборка B_j такая, что выполняются следующие условия.

1.Она составлена по результатам равноточных и взаимно независимых измерений.

2. Систематические ошибки измерения отсутствуют.

3. Случайные ошибки измерения описываются нормальным законом распределения вероятностей.

Пусть, далее, каждая выборка B_j является репрезентативной с вероятностью P^*≥ 0.95.

Обозначим

M_j = 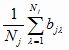и S_j =

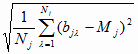
Говорят, что МР S при t = t₀ является заданным (определенным, известным), если задана совокупность

M_j(G); j = 1..n, (1.3)

где

M_j(G) – генеральное среднее арифметическое случайной величины M_j.

Если в момент времени t = t₀ совокупность величин (1.3) является известной, то можно говорить, что истина о МР S познана с вероятностью, равной 1.

Пусть, t_j – критическое значение критерия Стьюдента при заданной доверительной вероятности P^* и степени свободы (N_j – 1):

t_j = t(P^*, (N_j – 1)) (1.4)

Если совокупность условий 1-3 выполняется, то можно оперировать следующими противоположными неравенствами [21]:

│M_j - M_j(G)│< d_j t_j (1.5)

и

│M_j - M_j(G)│≥ d_j t_j (1.6)

где

d_j = S_j 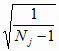(1.7)

Если имеет место (1.5), то с вероятностью P^* утверждают, что справедливо равенство

M_j(G) = M_j

Тем самым полагают, что в открытой области

A_j^* = (M_j(G) – Δ_j*, M_j(G) + Δ_j*)

все значения величины M_j являются практически друг от друга неразличимыми,

где

Δ_j^* = d_j t_j (1.8)

Вместе с тем, в закрытой области

A_j = [M_j(G) – Δ_j^*, M_j(G) + Δ_j^*],

согласно (1.5) и (1.6), друг от друга различаются следующие три значения величины M_j:

M_j = M_j(G) – Δ_j^* , M_j = M_j(G) и M_j = M_j(G) + Δ_j^*

Это означает, что в области A_j величина y_j фактически измеряется в единицах Δ_j^*. Но тогда и в остальной части области своего задания эта величина должна быть измерена в единицах Δ_j^*. В противном случае будет нарушено условие равно точности измерений. В итоге, при выполнении условий (1.5) или (1.6), величина y_j наиболее точно измерима не в единицах Δ_j(П), а в единицах

Δ_j^* ≥ Δ_j(П), (1.9)

где

Δ_j(П) – абсолютная ошибка измерительного прибора величины y_j.

Так как вообще

│M_j - M_j(G)│≥ 0,

согласно (1.5) и (1.7) имеет место

Δ_j^* > 0 (1.10)

Следовательно, если даже измерительная техника улучшится настолько, что выполнится условие

Δ_j(П) = 0,

то, все равно, согласно (1.9) и (1.10), величина M_j, как конкретное значение величины y_j, фактически всегда будет устанавливаться с отличной от нуля абсолютной погрешностью. В итоге, найти истинное значение M_j, т.е. величину M_j(G), в принципе невозможно. Это означает, что утверждение

M_j = M_j(G) (1.11)

всегда будет справедливым с вероятностью

P < 1,. (1.12)

где

P – вероятность познания истины в МР S при t = t₀.

То, что выполнение равенства (1.11) в принципе невозможно, а в реальности всегда имеет место

M_j ¹ M_j(G), (1.13)

еще более отчетливо видно из следующего.

По определению величины M(G) имеет место

M_j(G) = M_j при n → ∞, (1.14)

а по определению величины t_j имеем

t_j ≥ 0

С учетом последнего неравенства из (1.7), (1.8) и (1.10) получаем

S_j > 0 и N_j < ∞

Отсюда и из (1.14) имеем

M_j ¹ M_j(G),

т.е. получаем (1.13).

Следует обратить внимание на то что, всегда имеет место

S_j > 0; j = 1..n

Это означает, что каждая величина y_{j Î} Y в МР S имеет, как минимум, три различных возможных значения:

y_jmin, y_j0 = 0.5 (y_jmin + y_jmax) и y_jmax,

т.е. выполняется условие

N_j ≥ 3,

где

y_jmax > y_jmin

В итоге

S_j > 0 и 3 £ N_j < ∞ (1.15)

Из того факта, что найти величины (1.3) в принципе невозможно, следует, что познание истины об МР S с вероятностью, равной 1, является в принципе невозможным.

Это положение справедливо во всех случаях, когда выполняется совокупность условий 1 – 3. А эти условия являются естественными, т.е. они характеризуют процессы, происходящие в природе совершенно естественным образом [22]. Только человек может, например, сознательно нарушить условие 2.

В итоге, положение о невозможности познания истины с вероятностью 1, справедливо для любых естественных объектов, в том числе для простейших составляющих вещества.

В заключение отметим, что положение о невозможности познания истины с вероятностью, равной 1, в философии известно давно [23], а математически это положение впервые нами было доказано в [16,17]. Более того, в настоящее время установлен способ определения вероятностного предела познания истины [21, 24]. Тем не менее, попытки поиска простейших составляющих вещества продолжаются до сих пор [25].

1.6. Локальные единицы измерения показателей качества функционирования МР

Величина P, как видно, является важнейшей вероятностной характеристикой состояния МР S. При этом эта величина является функцией времени. Следовательно, функцией времени будет являться и состояние МР S, характеризуемое этой величиной.

Назовем состояние, характеризуемое величиной P, фактическим состоянием МР S.

Пусть, P₀ – наибольшее возможное значение P для МР S при t = t₀.

О величине P₀ говорят, что она является вероятностным пределом познания истины МР S при t = t₀.

Согласно (1.12) имеет место

P £ P₀ < 1 (1.16)

Пусть

M_j1, S_j1, N_j1, M_j0, S_j0 и N_j0; j = 1..n (1.17)

– значения величин

M_j, S_j и N_j; j = 1..n

такие, что

M_j = M_j1; S_j = S_j1 и N_j = N_j1; при P^* = P; j = 1..n

и (1.18)

M_j = M_j0; S_j = S_j0 и N_j = N_j0; при P^* = P₀; j = 1..n

Согласно (1.15) и (1.18) имеет место

S_j1> 0, S_j0 > 0, 3 £ N_j1< ∞ и 3 £ N_j0 < ∞ (1.19)

Обозначим

d_jk^* = S_jk 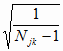и t_jk^* = t(P, (N_jk-1)); k = 0,1; j = 1..n

d _j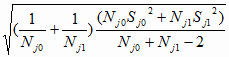^* = ; j = 1..n (1.20)

t _j^* = t (P, (N_j0 + N_j – 2)); j = 1..n,

где

t_jk^* - критическое значение критерия Стьюдента при доверительной вероятности P и степени свободы (N_jk – 2 );

t _j^*- критическое значение критерия Стьюдента при доверительной вероятности P₀ и степени свободы (N_j0 + N_j1 – 2 ).

Согласно (1.19) и (1.20) имеют место

d_jk^* t_jk^* > 0 и d _j^*.t _j^* > 0; j = 1..n (1.21)

Положим, что для выборок данных, по которым совокупность величин (17) установлена, выполняются условия 1 – 3. Пусть, при этом эти выборки являются репрезентативными с вероятностью P. Тогда можно оперировать следующими противоположными неравенствами [22]:

│M_jk - M_jk(G)│< d_jk^* t_jk^*; j = 1..n (1.22)

и

│M_jk - M_jk(G)│≥ d_jk^* t_jk^*; j = 1..n (1.23)

а также и совокупностью неравенств

│M_j1 - M_j0│< d _j^*.t _j^*; j = 1..n (1.24)

и

│M_j1 - M_j0│≥ d _j^*.t _j^*; j = 1..n (1.25)

где

M_jk(G) – генеральное среднее арифметическое M_jk.

Если имеет место (1.22), то с вероятностью P утверждают, что справедливо равенство

M_jk(G) = M_jk

Тем самим полагают, что в открытой области

A_jk^* = (M_jk(G) – Δ_jk*, M_jk(G) + Δ_jk*)

все значения величины M_jk являются практически друг от друга неразличимыми,

где

Δ_jk* = d_jk^* t_jk^* (1.26)

Вместе с тем, в закрытой области

A_jk^** = [M_jk(G) – Δ_jk^*, M_jk(G) + Δ_jk^*],

согласно (1.22) и (1.23), друг от друга различаются следующие три значения величины M_jk:

M_jk = M_jk(G) – Δ_jk^* , M_jk = M_jk(G) и M_jk = M_jk(G) + Δ_jk^*

Это означает, что в области A_jk^* величина y_j фактически измеряется в единицах Δ_jk^*. Но тогда и в остальной части области своего задания эта величина должна быть измерена в единицах Δ_jk^*. В противном случае будет нарушено условие равно точности измерений. В итоге, при выполнении условий (1.22) или (1.23), величина y_j наиболее точно измерима не в единицах Δ_j(П), а в единицах

Δ_jk^* ≥ Δ_j(П).

Если имеет место (1.22) и при этом выполняется и условие (1.24), то с вероятностью P утверждают, что справедливо равенство

M_j1 = M_j0

Тем самым полагают, что в открытой области

A_j^* = (M_j0 – Δ_j*, M_j0 + Δ_j0*)

все значения величины M_j1 являются практически неразличимыми от M_j0.

Вместе с тем, в закрытой области

A_j** = [M_j0 – Δ_j*, M_j0 + Δ_j0*)], (1.27)

согласно (24) и (25), друг от друга различаются следующие три значения величины M_j1:

M_j1 = M_j0 – Δ_j^* , M_j1 = M_j0 и M_j1 = M_j0 + Δ_j^*,

где

Δ_j^* = d _j^*.t _j^* (1.28)

Это означает, что в области A_j^** величина y_j фактически измеряется в единицах Δ_j^*. Но тогда и в остальной части области своего задания эта величина должна быть измерена в единицах Δ_j^*. В противном случае будет нарушено условие равно точности измерений. В итоге, при выполнении условий (1.24) или (1.25), величина y_j наиболее точно измерима не в единицах Δ_j(П), а в единицах

Δ_j^* ≥ Δ_j(П).

Поскольку выполнение условий (1.24) и (1.25) имеет смысл только в том случае, когда выполняется условие (1.22), казалось бы, в качестве единицы измерения, имеющей смысл для всех областей A_j1**, A_j0** и A_j**, должна служить величина

Δ_jmax^* = max{Δ_j0^*, Δ_j1^*, Δ_j^*} (1.29)

В действительности, однако, запись (1.29) не является корректной.

В самом деле, согласно (1.20), имеют место

d_j1^* = d_j0^* = S_j0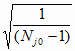 и t_j1^* = t_j0^* = t (P, (N_j0 – 1)) при S_j1 = S_j0 и N_j1 = N_j0

и (1.30)

d _j^* = S_j0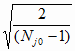 и t _j^* = t (P, 2 (N_j0 – 1)) при S_j1 = S_j0 и N_j1 = N_j0

С учетом этого из (1.26) и (1.28) получаем

Δ_j0^* =Δ_j1^*¹ Δ_j^* при S_j1 = S_j0 и N_j1 = N_j0

Как видно, при равных условиях, а точнее, когда

S_j1 = S_j0 и N_j1 = N_j0,

величины Δ_j0^* и Δ_j1^* принимают одинаковые значения и, следовательно, являются между собой сопоставимыми величинами. А величина Δ_j^* отличается от Δ_j0^* и Δ_j1^*и, следовательно, она не относится к величинам, сопоставимым с Δ_j0^* и Δ_j1^*.

В итоге, запись(29) не является корректной и, следовательно, ею пользоваться не следует.

Обозначим

d_jk = S_jk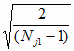 и t_jk = t (P, 2 (N_jk – 1)), (1.31)

где

t_jk - критическое значение критерия Стьюдента при заданной доверительной вероятности P₀ и степени свободы 2 (N_jk – 1 ):

Согласно (1.19), (1.20) и (1.31) имеем

Δ_j0 =Δ_j1 = Δ_j^* при Δ_j0^* =Δ_j1^*

Δ_j1 < Δ_j0 < Δ_j^* при Δ_j1^* < Δ_j0^* (1.32)

Δ_j0 < Δ_j^* < Δ_j1 при Δ_j0^* > Δ_j1^*,

где

Δ_jk = d_jk t_jk > 0 (1.33)

Обозначим

d _j = d_j1 и t _j = t_j1 при Δ_j1 ≤ d _j^*.t _j^*

и (1.34)

d _j = d _j^* и t _j = t _j^* при Δ_j1 > d _j^*.t _j^*

Согласно (1.21) и (1.34) имеет место

0 < d _j.t _j ≤ d _j^*t _j^* (1.35)

Обозначим

s _j = d _j t _j (1.36)

Можно проверить, что

s _j= Δ_j0 = Δ_j1 = Δ_j^* при Δ_j0^* = Δ_j1^*,

т.е. величины D _j, Δ_j0, Δ_j1 и Δ_j^* являются между собой вполне сопоставимыми.

При этом, согласно (1.34) и (1.35), имеет место

│M_j1 - M_j0│ < s _j Þ │M_j1 - M_j0│< d _j^*.t _j^*

Благодаря этому во всех случаях, когда

│M_j1 - M_j0│ < s _j, (1.37)

будет выполняться и условие (1.24) и, следовательно, с вероятностью P можно утверждать, что

M_j1 = M_j0.

Согласно (1.32), (1.34) и (1.36) имеет место

s _j £ Δ_j^* Û D _j1^* £ Δ_j0^*

Благодаря этому, при выполнении условия (1.37), согласно (1.22) и (1.26),всегда будет выполняться и условие

│M_jk - M_jk(G)│< d_j0^* t_j0^*

и, следовательно, с вероятностью P можно утверждать, что M_jk = M_jk(G).

Таким образом, выполнение условия (1.37) эквивалентно выполнению совокупности условий (1.22) и (1.24). Это означает, что с применением D _j в качестве единицы измерения величины y_jÎ Y всегда будет обеспечено принятие решения с вероятностью, равной P.

Совокупность величин

S_jk и N_jk; k = k₀; j = j₀; k₀ = 0,1; j₀ = 1..n

является характеристикой вполне определенного элемента МР S. Им является МР a_j Î S. Следовательно, и величина s _j должна служить характеристикой именно этой МР a_j Î S и только ее.

Принимая во внимание вышеизложенное, далее мы будем говорить, что D _j, является местной (локальной) единицей измерения величины y_jÎ Y в МР S при t = t₀.

Ясно, что

s _j ≥ D _j(п) > 0; j = 1..n,

где D _j(п) – абсолютная ошибка измерительного прибора, используемого при сборе данных

выборки B_j.

1.7. Нормальное состояние материальной реальности

Если

│M_j1 - M_j0│< s _j для всех j = 1..n,

то, как было показано выше, с вероятностью P.можно утверждать, что

M_j1 = M_j1(G), M_j0 = M_j0(G) и M_j1 = M_j0 для всех j = 1..n,

т.е. вообще

M_j1 = M_j1(G) = M_j0(G) для всех j = 1..n.

И это утверждение будет тем ближе к истине, чем меньшими будут величины

s _j; j = 1..N

Наиболее близким к истине это утверждение будет при

s _j = s _j0 для всех j = 1..n,

где s _j0 – минимально возможное значение Δ_j для МР S при t = t₀.

Следовательно, для вероятности познания истины P должна иметь место

P = P₀ Û s _j = s _j0 для всех j = 1..n (1.38)

Вообще для каждой материальной реальности S, согласно (1.16) и (1.38), должно иметь место [26]:

0< s _j0 £ s _j; j = 1..n, (1.39)

Пусть, фактическое состояние МР S при t = t₀ такое, что выполняется условие

s _j = s _j0 для всех j = 1..n, (1.40)

В этом случае все первичные показатели состояния МР S при t = t₀ могут быть измерены с наибольшей точностью и, следовательно, согласно (38), будет иметь место

P = P₀ (1.41)

Определение 1.5

Пусть, состояние МР S при t = t₀ такое, что имеет место (1.41) и, следовательно, согласно (1.38), выполняется условие (1.40).

Тогда и только тогда говорят, что МР S при t = t₀ находится в наилучшем – нормальном – состоянии [16,17].

О совокупности

M_j0; S_j0 и N_j0; j = 1..n

говорят, что она служит характеристикой нормального состояния МР S при t = t₀.

Понятие «Нормальное состояние», как видно, определено с помощью совокупности величин P и P₀.

Величины P и P₀ имеют смысл, как для объектов живой природы, так и для объектов неживой природы. Следовательно, введенное понятие нормального состояния является общим для объектов живой и неживой природы. Этим оно выгодно отличается от понятий нормального состояния, используемых в настоящее время в физике и биологии.

Можно показать, что понятия нормального состояния, используемые в биологии и физике, в действительности, являются частными случаями вышеприведенного.

В самом деле, согласно (1.18), имеет место

M_j = M_j1 = M_j0 при P^* = P = P₀

Согласно Р.М. Баевскому, живой организм находится в нормальном состоянии, если [26]:

y_j Î Y_j0 для всех j = 1..n, (1.42)

где

Y_j0 – область нормы величины y_jÎ Y для живого организма S при t = t₀:

Y_j0 = (M_j0 - s _{j 0}, M_j0 + s _j0); j = 1..n, (1.43)

Для того чтобы было выполнено условие (1.42), живой организм S при t = t₀, в первую очередь, должен обладать всеми соответствующими функциональными частями, т.е. он должен быть целым.

Таким образом, в нормальном состоянии живой организм всегда представляет собой целостное образование, т.е. число его функциональных частей всегда равно n. Это необходимое, но далеко не достаточное условие для того, чтобы живой организм находился в нормальном состоянии.

Кроме этого, должно выполняться следующее условие.

Обозначим

Y_j = (M_j0 - s _j, M_j0 + s _j); j = 1..n (1.44)

Об области Y_j говорят, что она является областью неразличимости значений величины y_jÎ Y от M_j0. Точнее, она является таковой при измерении величины y_jÎ Y в единицах Δ_j.

Чем уже будет ширина областей

y_j Î Y_j; j = 1..n,

тем более обоснованным будет решение, принимаемое в живом организме. А наименьшую ширину эти области, согласно (1.42), (1.43) и (1.44) будут иметь в том случае, когда

s _j = s _j0; j = 1..n

В итоге

y_j Î Y_j = Y_j0 Û s _j = s _j0; j = 1..n

Отсюда и из (1.38) находим

P = P₀ Û y_j Î Y_j = Y_j0 для всех j = 1..n

Таким образом, для живого организма зависимости (1.38) и (1.42) являются эквивалентными. Это означает, что понятие нормального состояния, введенное выше, совпадает с понятием нормального состояния, применяемым в биологии и медицине.

Для того чтобы человек находился в нормальном состоянии, в первую очередь, он должен быть здоровым. Больной человек по определению не может находиться в нормальном состоянии. Он может находиться или не находиться в состоянии покоя.

А если человек здоров, то он может поднять 50 кг и более груза и с ним ничего не случится. Другой дело, если человек болен, например, ишемической болезнью сердца. Такой человек, скорей всего, получит инфаркт даже при поднятии 10 кг груза.

Из выше изложенного следует, что в нормальном состоянии организм человека обладает наибольшими потенциальными возможностями. В физике, вместо словосочетания «Потенциальные возможности организма», применяют словосочетания: «Потенциальная энергия физического тела». При этом если потенциальная энергия физического тела наибольшая, то его кинетическая энергия, согласно закону полной энергии, должна быть наименьшей. Отсюда смысл определения: физический объект находится в нормальном состоянии, если его кинетическая энергия является наименьшей.

Итак, понятия нормального состояния, введенные в физике и медицине, являются частными обозначениями понятия нормального состояния, введенного выше.