Гл. 2 Система и ее элементы

2.1. Понятие системы

Пусть

A_j ⊂ A; j = 1..n

- непустые конечные множества материальных реальностей, а

H_j; j = 1..n

- непустые конечные множества отношений такие, что для каждой пары

S_j = < A_j, H_j > ; j = j₀; j₀ = 1..n

имеет место

S_j = S_j0 Û y_j = y_j0 Î Y,

а для пары S = < A, H > выполняется условие

S = S₀ Û Y = Y₀ ,

т.е. вообще имеют место

S = S₀ Û Y = Y₀ и S_j = S_j0 Û y_j = y_j0 для всех j = 1..n , (2.1)

где S₀, Y₀, S_j0 и y_j0 являются фиксированными значениями S, Y, S_j и y_j соответственно.

Определение 2.1

Пусть, имеет место (2.1) и при этом

2 £ n < ¥

и (2.2)

S = S₀ Û S_j = S_j0 для всех j = 1.. n

Тогда и только тогда говорят, что пара S является системой элементов

S_j; j = 1..n.

О каждой паре S_j говорят, что она является j –ой функциональной частью системы S.

Если n = 1, т.е. имеет место: S = S₁, то о паре S говорят, что она является элементом системы более высокого уровня.

О каждой паре S_j говорят также, что она является j –им функциональным элементом системы S

Определение 2.2

Пусть, пара S является системой, т.е. выполняется совокупность условий (2.1) и (2.2).

Тогда и только тогда говорят, что множество (1.1) является генеральной совокупностью первичных показателей состояния системы S .

2.2. Анатомические элементы системы

Пусть

a_s; s = 1..m; m ≥ 2 (2.3)

– множество материальных реальностей такое, что

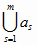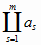= A и = Æ (2.4)

Определение 2.3

Пусть

h_s ¹ Æ ; s = 1..m

- множества отношений, заданные на множества (2.3) такие, что качество функционирования каждой материальной реальности

s = < a_s, h_s>; s = s₀; s₀ = 1..m (2.5)

описывается той же совокупностью первичных показателей, какою описывается качество функционирования всей самой системы S, т.е. имеет место

Y_s = Y; s = 1.. m, (2.6)

где

Y_s - генеральная совокупность первичных показателей качества функционирования МР s.

Тогда и только тогда о материальных реальностях

. s = 1.. m (2.7)

говорят, что они являются анатомическими элементами системы S.

Анатомические элементы системы S, согласно (2.4), не пересекаются между собой. Этим они принципиально отличаются от функциональных элементов этой системы.

Примерами анатомических элементов служат органы тела человека.

2.3. Точечные статистические и индивидуальные нормы

То, что качество функционирования каждой МР s описывается совокупностью показателей Y, указывает на то, что эта МР, со своей стороны, тоже является системой функциональных элементов, аналогичных к функциональным элементам системы S.

Пусть

M_j1(s); S_j1(s); N_j1(s); j = 1..n (2.8)

- значения величин.

M_j1; S_j1; N_j1; d _j и τ_j j = 1..n

такие, что

M_j1(s) = M_j1; S_j1(s) = S_j1; N_j1(s) = N_j1 при s = S; j = 1..n (2.9)

О величинах (2.8) говорят, что они являются характеристиками фактического состояния системы s при t = t₀.

Пусть, существует система s = 0 такая, что

M_j1(s) = M_j1(0); S_j1(s) = S_j1(0) и N_j1(s) = N_j1(0) при s = 0, (2.10)

где

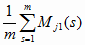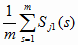M_j1(0) = ; S_j1(0) = и N_j1(0) = 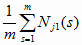; j = 1..n (2.11)

О системе s = 0 говорят, что она является типичным представителем (ТП) множества систем (2.7). Соответственно о величинах

M_j1(0); S_j1(0) и N_j1(0); j = 1..n (2.12)

говорят, что они являются характеристиками фактического состояния типичного представителя множества систем (2.7).

Система s = 0, как ТП совокупности систем (2.7), во-первых, является системой того же уровня, что и системы (2.7). Следовательно, качество функционирования этой системы, в отличие от качества функционирования системы S, сопоставимо с качеством функционирования любой системы из совокупности систем (2.7).

Во- вторых, система s = 0, как ТП совокупности систем (2.7), по сути дела, служит «лицом» всей большой системы S. Следовательно, по качеству функционирования системы s = 0 вполне можно судить о качестве функционирования самой системы S.

В итоге, изучая совокупность систем

s = 0.. m (2.13)

тем самим, по сути дела, мы будем изучать всю саму систему S.

Принимая во внимание выше изложенное, далее, вместо S, мы будем изучать именно совокупность систем (2.13).

Пусть

M_j0(s); S_j0(s) и N_j0(s); j = 1..n (2.14)

- значения величин (2.8) такие, что

M_j1(s) = M_j0(s); S_j1(s) = S_j0(s) и N_j1(s) = N_j0(s) при P = P₀; j = 1..n (2.15)

О величинах (2.14) говорят, что они с вероятностью P служат характеристиками нормального состояния системы s при t = t₀. При этом величины

M_j0(0); j = 1..n (2.16)

являются точечными статистическими нормами величин (1.1) для системы s при t = t₀.

Пусть

s _j(s) – значение s _j такое, что

s _j(s) = s _j при s = S; j = 1..n (2.17)

Согласно (1.20), (1.31), (1.33), (1.34) и (2.17) имеют место

d _j^*(s) =

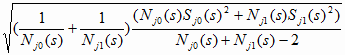
и (2.18)

t _j^*(s) = t (P, (N_j0(s) + N_j1(s) – 2)); j = 1..n,

d_jk(s) = S_jk(s)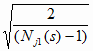

и (2.19)

t_jk(s) = t (P, 2 (N_jk(s) – 1)),

d _j(s) = d_j1(s) и t _j(s) = t_j1(s) при d_j1(s) t_j1(s) > 0 ≤ d _j^*(s).t _j^*(s)

и (2.20)

d _j(s) = d _j^*(s) и t _j(s) = t _j^*(s) при d_j1(s) t_j1(s) > d _j^*(s).t _j^*(s)

σ_j(s) = d _j(s) t _j(s) > 0 (2.21)

Обозначим

A_j(s) = [M_j0(0) - σ_j(s), M_j0(0) + σ_j(s)] (2.22)

Об области A_j(s) говорят, что она с вероятностью P служит областью статистической нормы величины y_j Î Y для системы s при t = t₀.

Определение 2.4

Пусть, величины (2.14) такие, что выполняется условие

M_j0(s) = M_j1(s) при M_j1(s) Î A_j(0)

и (2.23)

M_j0(s) = M_j0(0) при M_j1(s) Ï A_j(0),

где

A_j(0) = A_j(s) при s = 0

Тогда и только тогда о величинах (2.14) говорят, что они с вероятностью P служат индивидуальными характеристиками нормального состояния системы s при t = t₀. А о величинах

M_j0(s); j = 1..n (2.24)

говорят, что они являются точечными индивидуальными нормами величин (1.1) для системы (s) при t = t₀.

Все значения величины M_j1(s), для которых имеет место M_j1(s) Î A_j(0), согласно (2.22) и (2.24), являются практически неразличимыми от M_j0(s). Ввиду этого, казалось бы, вполне достаточно введение A_j(0) и нет необходимости введения M_j0(s). На самом деле, однако, введение M_j0(s) необходимо по следующим причинам.

1.Величина M_j0(s), являясь вполне определенным числовым значением y_j Î Y, служит объективной характеристикой состояния j –го элемента системы s в той мере, какою при M_j1(s) Î A_j(0) таковой служит величина M_j1(s).

2. Величина M_j0(s), как и величина M_j1(s), позволяет оперировать высшей шкалой измерений – шкалой отношений.

Иными словами, к величине M_j0(s) применимы все арифметические операции, чего нельзя сказать об области A_j(0).

3. Вообще для точечных индивидуальных норм, как естественных глобальных оптимумов, имеет место

M_j1(s) = M_j0(s) Û M_i1(s) = M_i0(s) для всех j,i = 1..n (2.25)

Зависимость (2.25) справедлива только для глобальных оптимумов и только для них.

Следовательно, если мы ограничимся рассмотрением одних областей

A_j(0); j = 1..n,

как это в настоящее время в медицине и биологии делают, то, тем самым, мы утеряем доступ к зависимости (2.25).

Итак, введение величин (2.24) нам позволяет:

1. Оперировать всеми арифметическими действиями.

2. Считаться с объективной реальностью, выраженной зависимостью (2.25).

2.4. Системные единицы измерения

Обозначим

a (s) = max{a _j(s); j = 1..n}, (2.26)

где

a _j(s) = 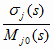(2.27)

Согласно (2.26) и (2.27) имеет место

0 < a ₀(s) £ a _j(s) £ a (s); j = 1..n; s = 1.m, (2.28)

где

a ₀(s) = min{a _j(s); j = 1..n }; s = 1.m (2.29)

Обозначим

Δ_j(s) = a (s) M_j0(s); s = 1.m; j = 1..n (2.31)

Согласно (2.27), (2.28) и (2.31) имеет место

Δ_j(s) ≥ s _j(s) = d _j(s) τ_j(s); s = 1..m; j = 1..n (2.32)

и, следовательно,

ç M_i1(s) – M_j0(s) ç ≥ Δ_j(s) Þ ç M_j1(s) - M_j0(s) ç ≥ d _j(s) τ_j(s) для всех j = 1..n (2.33)

В итоге, в том случае, когда для системы s существует хоть одно i = i₀ такое, что

ç M_i1(s) – M_i0(s)ç ≥ Δ_i(s); i = i₀; i₀ = 1.. n, (2.34)

согласно (2.33), будет иметь место

ç M_i1(s) – M_i0(s)ç ≥ d _i(s) τ_i(s); i = i₀; i₀ = 1.. n (2.35)

и, следовательно, не выполнится условие

ç M_i1(s) – M_i0(s)ç < d _i(s) τ_i(s); i = i₀; i₀ = 1.. n (2.36)

Согласно (2.18), (2.19), (2.20) и (2.21) имеет место

s _j(s) = f(P, S_i1(s), N_i1(s), S_i0(s), N_i0(s))

С учетом этого из (2.26), (2.27) и (2.31) получаем

Δ_j(s) = F(P, M_i1(s), M_i0(s) S_i1(s), N_i1(s), S_i0(s), N_i0(s); j = 1..n)

Как видно, величина Δ_j(s) содержит в себе сведения о состоянии всех функциональных элементов системы s, т.е. она является характеристикой всей системы s.

Принимая во внимание выше изложенное, о величине Δ_j(s) можно говорить, что она является объективной системной единицей измерения величины y_j Î Y в системе s при .

t = t₀.

Проверяя, выполняется или нет условие (2.36), тем самым, величину y_j Î Y, как было показано в главе 1, фактически мы измеряем в единицах σ_j(s). А проверяя, выполняется или нет условие (2.34), тем самым, величину y_j Î Y, фактически мы измеряем в единицах Δ_j(s). В связи с этим возникает вопрос: чем вызвана необходимость введения величин

Δ_j(s); j = 1..n (2.37)

Величины

a _j(s); j = 1..n,

согласно (2.27), являются относительными ошибками измерений величин, служащих первичными показателями качества функционирования системы s.

Если

a _j(s) = a _i(s) для всех j,i = 1..n, (2.38)

то в системе s измерения производятся с одной и той же относительной точностью. Именно так происходит, когда система s находится в нормальном состоянии, т.е. когда

p(s) = p₀(s), (2.39)

где

p(s) – вероятность фактического познания истины в системе s при t = t₀;

p₀(s) – вероятностный предел познания истины в системе s при t = t₀.

Если условие (2.38) не выполняется, то имеет место

a ₀(s) < a (s)

В этом случае выполнение условия равно точности измерений можно обеспечить двумя путями.

Путь 1.

Уравнять величины

a _j(s); j = 1..n (2.40)

таким образом, чтобы имело место

a _j(s) = a ₀(s) для всех j = 1..n

Путь 2

Уравнять величины (2.40) таким образом, чтобы имело место

a _j(s) = a (s) для всех j = 1..n} (2.41)

При выборе первого пути система s ошибочно будет считать, что она находится в нормальном состоянии, а на самом деле она не будет находиться в нормальном состоянии. Следовательно, этот путь исключен. В итоге, остается путь 2, когда выполняется условие (2.41).

Из (2.27), (2.28) и (2.41) имеем

Δ_j(s) = a (s) M_j0(s); s = 1.m; j = 1..n,

т.е. получаем (2.31).

Итак, одна из причин введения величин (2.37) является необходимость обеспечения равно точности измерений. Имеется и другая, не менее важная причина. О ней речь будет идти в главе 4

Обозначим

MO_j1(s) = Round(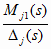,0) d _j(s) (2.42)

Как видно, величина MO_j(s) измеряется в единицах d _j(s) и, следовательно, имеет место

│M_j1(s) – MO_j1(s)│ > 0 при d _j(s) > s _j(s), (2.43)

т.е. в общем случае величина MO_j1(s) отличается от M_j1(s).