Данная информация предназначена для специалистов в области здравоохранения и фармацевтики. Пациенты не должны использовать эту информацию в качестве медицинских советов или рекомендаций.
Гл.3.
Целостная система и ее аналитические и
вероятностные характеристики
3.1. Понятие целостной системы
Далее, вплоть до главы 6, будем полагать, что
s = s0;
s0 = 0.. m
Это позволяет оперировать обозначениями
a, h, p, a , a
j, Δj,
MOj1 и Mj0;
j = 1..n,
где
a = as, h = hs p= p(s), a =
a (s), a j =
a j(s),
Δj =
Δj(s),
MOj1 = MOj1(s)
и Mj0
= Mj0(s)
при s =
s0 (3.1)
Ввиду того, что
h ¹ Æ
, (3.2)
элементы системы s, в отличие от элементов множества a,
всегда являются взаимно связанными. Эта
взаимосвязанность выражается в том, что процессы, происходящие в элементах
системы s, являются в
той или иной, отличной от нуля,
степени согласованными.
Вообще, если выполняется условие (3.2), то можно
говорить, что система s
является в той или иной, отличной от нуля,
степени целостной. В противном случае можно
говорить, что система s не является целостной. Например, труп скорей всего не
является целостной системой.
Согласно В.Г. Афанасьеву главным признаком
целостности системы s
является наличие у этой системы т.н. единого интегративного качества
(ЕИК) [13, 14].
Под ЕИК системы s
понимают качество, которое этой системой
проявляется в той мере, в какой это качество проявляется каждым ее
функциональным элементом, т.е. имеет место
g = g 0
Û g j
= g 0 для
всех j = 1..n, (3.3)
где
g - аналитическая
мера проявления ЕИК системой s: 0 £
g £ 1;
g 0 –
фиксированное значение g ;
g j –
аналитическая мера проявления ЕИК
j –им функциональным
элементом системы s.
Вторым важным признаком целостности системы s.,
согласно В.Г. Афанасьеву, является ее историчность,
т.е. то, что для этой системы условие
g > 0 (3.4)
выполняется в течение вполне определенного интервала времени от t1
до t2.
Определение 3.1
Пусть, в момент времени t = t0
(t1 £ t0 £
t2) условие (3.3) выполняется,
где
t0 – фиксированное значение t.
Пусть, при этом в момент времени t = t0
имеет место неравенство (3.4).
Тогда и только тогда говорят, что система s. на
изменение среды своего существования
в момент времени t = t0
реагирует как единое целое.
Под средой существования системы s
понимают совокупность внутренних и внешних факторов
(условий), при которой имеет место неравенство (3.4).
Любая другая среда не является средой
существования системы s. и, следовательно, она на изменение такой среды не может
реагировать как единое целое.
Определение 3.2
Пусть, система s. в момент времени t = t0
(t1 £ t0 £
t2) на изменение среды своего
существования реагирует как единое целое.
Тогда и только тогда говорят, система s в момент
времени t = t0 является
целостной системой.
О величине g
0 говорят, что она является
фактическим значением
g при t = t0.
Говорят также, что g
0 является характеристикой
фактического состояния целостной системы
s в момент времени
t = t0.
Если g =
g 0 = 1, то
можно говорить, что целостная система s в момент времени t = t0
находится в наилучшем – нормальном –
состоянии. А вообще о величине
g можно говорить, что она является мерой соответствия (близости)
фактического состояния целостной системы s
ее возможному в момент времени t = t0
нормальному состоянию.
Аналогично, о величине g
j можно
говорить, что она является мерой соответствия (близости) фактического
состояния j -го
функционального элемента целостной
системы s его возможному в момент времени t = t0
нормальному состоянию.
Итак, мера проявления ЕИК и мера
соответствия (близости) фактического состояния возможному нормальному состоянию
– два различных названия одной и той же величины. Первое название, быть может,
имеет смысл применять в среде философов, а второе – в среде биологов, медиков,
инженеров, социологов и физиков.
3.2. Предельно допустимые значения первичных
показателей
качества функционирования ЦС
Величина MOj1
по определению измеряется в единицах
D j.
Следовательно, с точностью D
j > 0
можно утверждать, что
MOj1 = Mj0
при │MOj1
- Mj0│< D
j
и, в конечном счете,
g j = 1
при │MOj1
- Mj0│< D
j (3.5)
Определение 3.3
Пусть, в момент времени t = t0
система s
является целостной и, следовательно, согласно (3.4)
и (3.5), имеет место
0 < g
min £ g
£ 1, (3.6)
где
g min –
минимально допустимое
в момент времени t = t0
значение g для целостной
системы s.
Пусть, далее
ajmin и
ajmax; j = 1..n
(3.7)
- значения величин
yj Î
Y; j = 1..n
(3.8)
такие, что
g j = 1
при │MOj1
- Mj0│< D
j
и g jmin
< g j < 1
при │MOj1
- Mj0│≥ D
j и 0
< D
j ≤ ajmin ≤
MOj1 ≤ ajmax
< ∞ (3.9)
g j =
g min > 0
при MOj1
< ajmin или
MOj1 > ajmax
и, следовательно, вообще имеет место
0 < D
j ≤ ajmin ≤
MOj1 ≤ ajmax
< ∞ для всех
j = 1..n (3.10)
Тогда и только тогда говорят, что величины (3.6)
для ЦС s. в момент
времени t = t0 являются
системными минимально и максимально
допустимыми значениями величин (3.7)
соответственно.
Величины
Mj0; j =
1..n
являются конкретными значениями величин
MOj1; j =
1..n
Следовательно, и для них должна иметь место
зависимость
0 < D
j ≤ ajmin ≤
Mj0 ≤ ajmax
< ∞;j = 1..n
(3.11)
Согласно (3.10) имеет место
0 < D
j ≤ ajmin; j
= 1..n
Это условие будет выполняться, если положим, что вообще
ajmin = D
j; j = 1..n
(3.12)
Пусть, совокупность условий (3.10) и (3.12)
справедлива для любых ЦС, включая целостную систему, для которой каждая из
величин (3.7) имеет всего три возможных значения:
yj1 = D
j; yj2
= 2 D j
и yj3
= 3 D j
Тогда из (3.11) и (3.12)
получим:
ajmin = D
j; Mj0
= 2 D j
и ajmax =
3 D j;
j = 1..n (3.13)
Отсюда следует, что вообще
Mj0 =
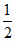 (ajmin
+ ajmax); j = 1..n
(3.14)
(ajmin
+ ajmax); j = 1..n
(3.14)
и, следовательно,
ajmax = 2 Mj0
- ajmin; j = 1..n
(3.15)
и, в конечном счете, согласно (3.12),
ajmax = 2 Mj0 - D
Oj; j = 1..n (3.16)
Обозначим
aj = ajmin при MOj1
£ Mj0 и aj
= ajmax при MOj1 > Mj0
(3.17)
О величине aj
говорят, что она является системным
предельно - допустимым значением величины
yj Î
Y в ЦС
s при t = t0
Обозначим
Cj = ç 1 -
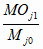 ç
, если D
j ≤ ç
Mj0 - MOj1ç
≤ ç Mj0
- ajç
ç
, если D
j ≤ ç
Mj0 - MOj1ç
≤ ç Mj0
- ajç
Cj = a ,
если ç
Mj0 - MOj1ç
> ç Mj0
- aOjç ;
j = 1..n (3.18)
Cj = 1 - a ,
если ç
Mj0 - MOj1ç
< D
Oj,
Согласно (2.31), (3.1)(3.12) и (3.15) имеет
место
ajmin = a
Mj0 и
ajmax = (2 - a
) Mj0 (3.19)
С учетом этого из (3.17) и (3.18) получаем
a ≤ Cj ≤ 1 -
a , если
a ≤ ç 1 -
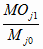 ç
≤ (1 - a )
ç
≤ (1 - a )
Cj = a ,
если ç 1 -
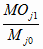 ç
> (1 - a )
ç
> (1 - a )
Cj = 1 - a ,
если ç 1 -
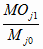 ç
< a ,
ç
< a ,
т.е. вообще имеет место
a ≤ Cj ≤ 1 -
a ; j = 1..n
(3.20)
Обозначим
C = max{Cj;
j = 1..n} (3.21)
Согласно (3.20) и (3.21) имеем
0 < a ≤
C ≤ (1 - a ) (3.22)
Отсюда
0 < a ≤ (1 -
a ),
т.е. вообще имеет место
0 < a ≤ 0.5 (3.23)
Согласно (2.31), (3.1) и (3.23) имеет место
2 D j ≤
Mj0 , (3.24)
а согласно (3.10) и (3.12) имеем
D j ≤
MOj1 (3.25)
Пусть, для системы
s в момент времени
t = t0.выполняется
условие
0 < D
j = ajmin ≤
MOj j1 ≤ ajmax
< ∞ для всех
j = 1..n (3.26)
Тогда из (3.7) и (3.9) получим
g > 0,
т.е. будет выполняться условие (3.4), указывающее на то, что система
s. в момент времени
t = t0
находится в среде своего существования.
Итак, если выполняется условие (3.26), то с
вероятностью p (0.5 ≤ p ≤
p0 <1) утверждают
что система s.
в момент времени t =
t0 находится
в среде своего существования.
3.3. Вероятность
адекватной реакции целостной системы на изменения
среды своего существования.
Согласно (3.22) имеет место
C ≤ (1 - a )
Это условие будет выполняться, если положим, что вообще
C = 1 - a (3.27)
Отсюда и из (3.23) имеем
0.5 ≤ C < 1 (3.28)
Каков смысл совокупности зависимостей (3.23),
(3.27) и (3.28)?
Чтобы ответить на этот вопрос, в первую очередь
необходимо выяснить, что следует понимать под адекватной реакцией целостной
системы на изменение среды ее существования?
Определение 3.4
Пусть, реакция системы s
на изменение среды своего существования в
момент времени t = t0
(t1 ≤ t0 ≤
t2) такова, что
в момент времени
t0 +D
t; D t
> 0; D t ®
0
выполняется условие
p(t0) ≤
p(t0 +
D t)
при p0(t0)
≤ p0(t0 +
D t)
или (3.29)
p(t0) >
p(t0 +
D t)
при p0(t0)
> p0(t0 +
D t)
где
p(t0) –
вероятность
познания истины в системе
s. в момент времени
t = t0;
p(t0 +D
t) – вероятность познания
истины в системе s.
в момент времен t =
t0 +D
t;
p0(t0) –
максимально возможное значение
p(t0)
для системы s.
в момент времени t =
t0;
p0(t0 +D
t) – максимально возможное
значение p(t0 +D
t) для системы
s.в момент времени
t0 +D
t ;
Тогда и только тогда говорят, что система
s. на изменение среды своего
существования в момент времени t =
t0 (t1 ≤ t0
≤ t2) реагирует
адекватно, и пишут:
p(t0) =
p < 1 , (3.30)
где
p – вероятность того, что
система s в момент
времени t = t0
на изменение среды своего существования
реагирует адекватно.
Если условие (3.29) не
выполняется, то говорят, что система
s. на изменение среды своего
существования в момент времени t =
t0 (t1 ≤ t0
≤ t2) реагирует
неадекватно.
Как видно, понятия: «Вероятность адекватной
реакции» и «Вероятность познания истины» являются синонимами.
Пусть, p*
- вероятность того, что в момент времени
t = t0
система s.
на изменение среды своего существования
реагирует неадекватно.
По определению величин p
и p*
имеет место
p + p* = 1 (3.31)
Отсюда и из (3.30) имеем
0 < p* ≤ 0.5 и
0.5 ≤ p < 1 (3.32)
Сопоставляя совокупность зависимостей (3.17),
(3.27) и (3.28) с совокупностью зависимостей (3.31) и (3.32), заключаем
C = p
и a =
p* (3.33)
Таким образом, величины C
и a являются
вероятностными характеристиками
целостных систем [18,19]. Но тогда и величины
a j
и Cj;
j =1..n,
согласно (2.26), (3.1) и (76), должны являться вероятностными
характеристиками соответствующих функциональных частей целостных систем и,
следовательно, должно иметь место
Cj = pj;
j =1..n, (3.34)
где
pj -вероятность
фактического познания истины в j –ем функциональном элементе системы
s в момент времени
t0 = t0.

