Данная информация предназначена для специалистов в области здравоохранения и фармацевтики. Пациенты не должны использовать эту информацию в качестве медицинских советов или рекомендаций.
Гл. 5. Количественное измерение
единого интегративного качества
5.1.Измерение ЕИК элементов ЦС
Обозначим
dj = + 1, если
MOj1≤ Mj0
и
(5.1)
dj = - 1, если
MOj1 > Mj0
Согласно (3.17) и (5.1) имеет место
ajmin ≤ MOj1
≤ ajmax Û
ç Mj0 -
MOj1ç
b j1 ≤
ç Mj0 -
aj ç ,
(5.2)
где
b j1 = 1,
если (MOj1
- aj) dj
³ 0
и
(5.3)
b j1 = 0,
если (MOj1
- aj) dj < 0
Обозначим
g j*
= 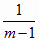 ((m - 2 ) b
j + 1), (5.4)
((m - 2 ) b
j + 1), (5.4)
где
b j = 1
при ç
MOj1 - MOj0ç
< Δj
b j =
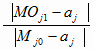 b j1
при ç
MOj1 - ajç
b j1
£ ç MOj0
- ajç
и ç
MOj1 - Mj0ç
≥ Δj
(5.5)
b j1
при ç
MOj1 - ajç
b j1
£ ç MOj0
- ajç
и ç
MOj1 - Mj0ç
≥ Δj
(5.5)
b j = 0
при ç
MOj1 - ajç
b j1 >
ç MOj0 -
ajç
Из (5.4) и (5.5) получаем
g j* = 1,
при ç
MOj1 - Mj0ç
< Δj
g *min,
< g j* < 1
при ç
MOj1 - ajç
b j1
£ ç MOj0
- ajç
и ç
MOj1 - Mj0ç
≥ Δj
(5.6)
g j*=
g *min,
при ç
MOj1 - ajç
b j1 >
ç MOj0 -
ajç
где
g *min
= 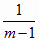 (5.7)
(5.7)
При этом, согласно (4.7) и (5.7), имеет место
0 < g *min
(5.8)
Согласно (5.2) должно иметь место
ç MOj1
- ajç
b j1 >
ç MOj0 -
ajç
Þ MOj1
£ ajmin
или MOj1
≥ ajmax (5.9)
С учетом (5.2), (5.8) и (5.9) зависимость (5.6) можно переписать в виде
g j* = 1
при ç
MOj1 - Mj0ç
< Δj
g *min,
< g j* < 1
при ç
MOj1 - Mj0ç
≥ Δj
и ajmin ≤
MOj1 ≤ ajmax
(5.10)
g j*=
g min > 0
при MOj1
£ ajmin
или MOj1
≥ ajmax
Совокупность зависимостей (3.8), (3.9), (5.8) и
(5.9) будет выполняться, если положим, что вообще
g j =
g j*
и g
min = g *min
(5.11)
С учетом (5.11) зависимость (5.4) можно
переписать в виде
g j =
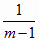 ((m - 2 ) b
j + 1); j – 1..n
((m - 2 ) b
j + 1); j – 1..n
и, в конечном счете, согласно (4.21),
g j = (1 – p((1
- b j);
j – 1..n (5.12)
5.2. Теория П.К. Анохина и измерение единого
интегративного качества ЦС
По теории П.К.Анохина [30- 32] за получение «желаемого
конечного результата» в каждый момент
времени t в организме
человека ответственность несет вполне определенная функциональная система
s(t).
Следовательно, для того, чтобы организм
s мог существовать и
продолжать двигаться к «желаемому конечному результату», в момент времени t
должны выполняться следующие условия
yj Î
Y(t) Û
0 < g j(t)
< 1; j =1..n(t),
(5.13)
и
0 < g j(t)
< 1 для всех j =1..n(t),
(5.14)
где
Y(t) – подмножество
Y, служащее
харктеристикой качества функционирования системы s(t):
Y(t) = Y
при s(t)
= s (5.15)
g j(t) –
значение g
j в момент
времени t:
g i(t) =
g i
при t = t 0; j = j0; j0
= 1.. ..n(t ); (5.16)
t 0 – некоторое фиксированное
значение t;
n(t) –объем
Y(t): n(t) £
n.
В самом деле, для организма живого человека, как
выраженной целостной системы, согласно (3.3) и (3.4), должно иметь место:
g i(t)
³ g
imin > 0; для всех
j =1.. ..n(t),
Следовательно, если хоть для одной величины g
i(t)
имеет
место
g i(t) = 0,
то это означает, что система
s(
t)
принадлежит организму мертвого
человека. А такая система, разумеется, не может
нести какой- либо ответственности.
Таким образом, выполнение условия
0 < g j(t)
для всех j =1.. ..n(t)
необходимо для того, чтобы система
s(t)
смогла справиться со стоящей перед ней задачей:
выполнять все без исключения функции
yj Î
Y(t); j = 1..n(t).
Что касается условия
g j(t) < 1
для всех j =1..n(t),
то его выполнение необходимо для того, чтобы существовали цели
g i(t)
® 1; j = 1.. ..n(t)
(5.17)
В самом деле, пусть выполняется условие
g i(t) = 1
при t = t 0; j =
j0; j0 = 1.. ..n(t)
Тогда, согласно (5.5) и (5.12) будет иметь место неравенство
ç MOj1
- Mj0ç <
Δj,
указывающее, что функциональная часть организма
s,
характеризуемая величиной yj
Î Y(t),
в момент времени t находится в нормальном состоянии
и, следовательно, она не выполнят никакой работы. Для того, чтобы эта часть не
находилась в покое, а выполняла работу, в первую очередь, должна существовать
необходимость выполнения этой работы. Иными словами, должна существовать цель
g i(t)
→ 1 при t =
t 0; j =
j0; j0 = 1..n(t)
А такая цель может существовать в том и только том случае, когда
0 < g j(t)
< 1 при t =
t 0; j =
j0; j0 = 1..n(t),
где
g (t) - значение
g такое, что
g (t) = g
при s(t) =
s (5.18)
О величине g
(t) говорят, что она является мерой проявления ЕИК
системой s(t).
Вообще, как указывалось выше, система
s(t) сможет справиться со
стоящей перед ней задачей: в том и только в том случае, когда будут выполняться
все без исключения функций
yj Î
Y(t); j = 1..n(t).
Ввиду этого цели (5.16) и являются равно
важными подцелями общей цели
g (t) ® 1
В итоге, смысл совокупности зависимостей (5.9) и
(5.10): их справедливость является необходимым и достаточным условием для того,
чтобы система s(t) cмогла
справиться со стоящей перед ней задачей, т.е. было достигнуто выполнение условия
g (t) = 1 при
g j(t) = 1
для всех j =1..n(t)
(5.19)
Вообще условие (5.19) будет выполняться, если
положим, что
g (t) =
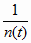
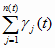 ,
(5.20)
,
(5.20)
Однако, для того, чтобы выполнялось условие
(5.19), в первую очередь, согласно (3.3), (3.4) и (5.18), должно выполняться
условие
g (t) > 0 при
g j(t) > 0
для всех j =1..n(t)
(5.21)
А это условие при справедливости (5.20) не выполняется. Оно выполнимо в том
случае, когда
g (t) =
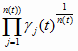 (5.22)
(5.22)
В этом случае будет выполняться и условие (5.19).
Перепишем зависимость (5.22) в более удобном
виде.
Обозначим
m(t) = 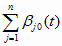 ; (5.23)
; (5.23)
где
b j0(t) = 1
при yj
Î Y(t)
и
(5.24)
b j0(t) = 0
при yj
Ï Y(t)
Согласно (5.13) и (5.24) имеет место
b j0(t) = 1
при 0 < g
j(t) < 1
и
j =1..
n(
t)
(5.25)
b j0(t) = 0
при g
j(t) = 1,
т.е. вообще
b j0(t) = 0
Û g j(t)
= 1 j =1..n(t)
(5.26)
В итоге, из (5.14), (5.25) и (5.26) имеем
b j0(t) = 1
при j = 1..n(t)
и (5.27)
b j0(t) = 0
при j = n(t)
+ 1, n(t) + 2,…,n
С учетом (5.27) из (5.23) получаем
m(t) = n(t)
£ n (5.28)
Отсюда и из (5.19) и (5.27) находим
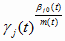 =
=
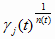 при j = 1..n(t)
при j = 1..n(t)
и
(5.29)
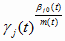 = 1
при j = n(t)
+ 1, n(t) + 2,…,n
= 1
при j = n(t)
+ 1, n(t) + 2,…,n
С учетом (5.26) и (5.27) зависимость (5.20)
можно переписать в виде
g (t) =
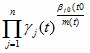 (5.30)
(5.30)
Пусть
m(t) = m = 0
при t = t0 (5.31)
Согласно (5.23) и (5.31) имеем
b j0 = 0
для всех j = 1..n,
где
b j0(t0)
= b j0
при t = t0
Отсюда и из (5.30) получаем
g (t0) =
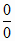
Таким образом, в том случае, когда выполняется
условие (5.31), зависимость (5.30) не применима.
Вместе с тем, в этом случае, согласно (5.14),
(5.16), (5.23) и (5.26), имеет место
g j = 1
для всех j = 1..n
Эта зависимость указывает на то, что в момент времени t = t0
система s
находится в нормальном состоянии, т.е. имеет место
g = 1 при
m = 0
Отсюда смысл следующей зависимости
g = 1 при
m = 0
и
(5.32)
g =
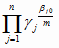 при m ≥ 1,
при m ≥ 1,
где
m =
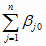
В заключение обратим внимание на то, что,
согласно (5.12) и (5.32) имеет место
g = g
min = 1 – p при
b j0 = 0
для всех j = 1..n
и, следовательно, согласно (4.17), выполняется условие
0 < g min
£ 0.5
При этом
g min = 0.5
Û p = 0.5
Полный алгоритм определения величины
g опубликован в [33 – 35].

