Данная информация предназначена для специалистов в области здравоохранения и фармацевтики. Пациенты не должны использовать эту информацию в качестве медицинских советов или рекомендаций.
Глава 11. Статистическое регулирование экспертных оценок качества
медицинских услуг
В отечественном здравоохранении многие специалисты предлагают
устранить недостаток информации с помощью более энергичных и усложненных форм
оценок показателей качества медицинской помощи, часто с использованием новых и
мощных компьютерных технологий. Ожидается, что большая информированность должна
привести к более последовательному и рациональному поведению, как
производителей, так и потребителей медицинских услуг. Поддерживаемые в настоящее
время органами управления здравоохранением мероприятия по разработке и
распространению технологических стандартов могут помочь информировать
растерявшуюся общественность в вопросах контроля над результатами деятельности
различных сфер практической медицины.
Сегодня имеется реальная возможность на нынешнем этапе
проведения модернизации отрасли избежать тех стратегических ошибок, которые
ввергли систему здравоохранения США в дорогостоящий процесс всемерного надзора
за качеством, борьбы между производителями и потребителями и, в конечном итоге,
сформировали тенденцию застоя. Многие специалисты по управлению здравоохранением
в России считают, что акцент на экспертные оценки и рациональное потребление
ресурсов в ЛПУ, несмотря на существенный сдвиг в сторону формировании стратегии
повышения качества и эффективности, пока не даёт ожидаемого эффекта.
В рамках повседневной экспертной работы специалисты
столкнулись с проблемой измерения наиболее важных показателей процесса оказания
медицинской помощи, что зачастую является даже более сложной задачей, чем оценка
результатов лечения. «Ключевые показатели процесса» - это такие показатели
процесса производства медицинских услуг, которые самым тесным образом связаны с
достижением желаемых результатов и удовлетворением потребностей пациента. Не
привыкшие систематически оценивать результаты лечения, руководители многих ЛПУ еще меньше знакомы с измерением
параметров процессов лечения. Кроме того, оценка результатов лечения без
измерений параметров процесса – это попытка оценок за пределами математических
правил и закономерностей.
Сегодня отечественное здравоохранение может позаимствовать у
промышленности простые методы измерения и представления тех показателей процесса
производства медицинских услуг, которые обусловлены введением изменений в рамках
программы модернизации. Основные средства измерения уровня качества производимых
услуг включают в себя такие простые математические процедуры, как расчеты
относительных и средних величин, их ошибок, измерения связи между явлениями в
рамках расчета коэффициента корреляции и т.п. Кроме того для этого же используются графические
приемы, такие как построение поточных диаграмм, гистограмм и текущих карт, а
также более сложные методы, как карты контроля, которые могут помочь любому
врачу и заведующему отделением с минимальной математической подготовкой понять
сущность измерения уровня качества на основании стандартного статистического
исследования. Эти математические методы и графические средства, а также
положительное отношение к оценкам, как результата лечения, так и процесса
работы, должны стать частью «клинического арсенала» врача, относящего себя к
медицинской школе будущего.
11.1. Элементы
теории вероятностей и математической статистике
Статистка – это отрасль
математики, которая изучает вопросы накопления (сбора), анализа, интерпретации и
наглядного представления числовых данных. Математическая статистика служит для:
определения,
установления или
описания
полученных
данных;
возможности
заключения
относительно
популяции или
генеральной
совокупности, из
которой сделана
выборка.
Медицинская (или санитарная) статистика представляет собою
одну из ветвей статистической науки и изучает явления общественной жизни,
связанные с медициной, гигиеной, санитарией и здравоохранением. Медицинская
статистика делится обычно на два основных раздела:
1. Статистика здоровья населения, к задачам
которой относится:
- изучение
состояния здоровья населения
(воспроизводство населения,
продолжительность жизни,
заболеваемость, физическое
развитие и др.);
- выявление и
установление связей между
уровнем заболеваемости и
смертности населения с
различными факторами окружающей
среды
.
2. Статистика здравоохранения, задачами
которой являются:
определение
показателей, характеризующих
качество работы
лечебно-профилактических
учреждений и отдельных врачей и
позволяющих объективно оценивать
их деятельность;
сбор и
изучение данных о сети, кадрах и
деятельности медицинских
учреждений, необходимых для
планирования здравоохранения и
контроля за выполнением планов;
статистическое исследование
мероприятий по предупреждению и
лечению заболеваний.
Испытание (эксперимент, опыт) - воспроизводимая совокупность условий, при
которых фиксируется тот или другой результат. О всяком новом испытании говорится
как о повторении прежнего, чтобы лишний раз подчеркнуть, что испытания
происходят в одних и тех же условиях.
Результат испытания называют событием. События обозначают большими буквами А, В,
С и т.д.
Если при повторении испытания его результаты могут отличаться
друг от друга, т.е. могут произойти события А, В, С и т.д., то о результате
испытания говорят как о случайном событии.
Случайной величиной – называется переменная величина, которая в
результате испытаний может принять то или иное значение в границах определенного
интервала.
Для количественной оценки возможности случайного события
пользуются понятием вероятности. Существует классическое и статистическое
определение вероятности. По классическому определению вероятностью события
А называется отношение
числа случаев m, благоприятствующих этому событию, к числу n всех возможных
случаев при данном испытании, т.е.
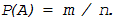 (11.1)
(11.1)
Формула (11.1) позволяет находить вероятность появления
элементарных событий. Чаще всего приходится определять вероятности сложных
событий по вероятностям элементарных событий.
Если при каждом испытании происходит событие А, то такое
событие называется достоверным. Если в условиях данного испытания событие
В заведомо не может произойти, то оно называется
невозможным.
Очевидно, что вероятность достоверного события равна единице,
вероятность невозможного события равна нулю, вероятность случайного события
лежит в пределах от нуля до единицы.
Случайные события называются несовместными в данном испытании, если никакие
два из них не могут появиться вместе.
Вероятность суммы несовместных событий А и В, т.е. того, что произойдет или событие А
или событие В равна
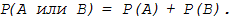 (11.2)
(11.2)
Формула (12.2) справедлива для любого числа несовместных
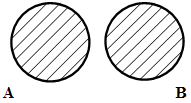
событий. По аналогии с теорией множеств выражению (12.2) соответствует
объединительное множество (рис.11.1).
События образуют полную группу, если в результате испытания непременно
должно появиться хотя бы одно из них. Два события А и А1 называются
противоположными,
если они несовместны и образуют полную группу. Сумма вероятностей
противоположных событий равняется единице.
Событие А называется независимым от события В, если вероятность появления
события А не зависит от того, произошло событие В или не произошло.
Если случайные события А и В независимы, то вероятность
одновременного наступления событий А и В (т.е.
вероятность того, что произойдет и событие А и событие В) равна произведению
вероятностей появления событий А и В:
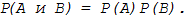 (11.3)
(11.3)
Формула (11.3) справедлива и для нескольких независимых
событий. По аналогии с теорией множеств зависимость (12.3) представляет собой
множество пересечения (рис.11.2).
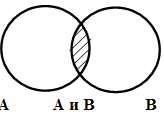
Вероятность суммы совместных событий А и В,
т.е. вероятность того, что произойдет
событие А или событие В или оба события вместе вычисляется по формуле
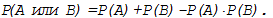 (11.4)
(11.4)
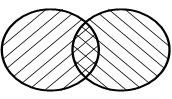
Графически это можно изобразить как на рис.1.3. Формулу типа
(12.4) можно вывести и для более чем двух совместных событий.
По формуле (11.4) имеем: P(B) = 0,1 + 0,2 - 0,1.
0.2=0,28. Вероятность
P(B) можно найти и пользуясь формулами (11.2) и (11.3). Пользуясь классическим
определением понятия вероятность, можно вычислить вероятность какого-либо
события теоретически, не прибегая к опыту. Однако на практике это не всегда
выполнимо. По этой причине в приложении теории вероятностей к вопросам контроля
качества часто пользуются так называемым статистическим определением
вероятности, значения которой можно получить после проведения испытаний.
Со статистической вероятностью тесно связано понятие
относительной частоты
события А, которая представляет собой отношение частоты появления m* события А к общему числу
произведенных испытаний n*, т.е.
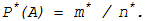 (11.5)
(11.5)
При небольшом n* частота события носит в значительной мере
случайный характер. Однако при увеличении n* частота все больше теряет свой
случайный характер: она проявляет тенденцию стабилизироваться, приближаясь, с
незначительными колебаниями, к некоторой средней постоянной величине, которая и
будет приближенно равна вероятности события. Вычисленную таким образом
вероятность называют статистической вероятностью, т.к. она получена в результате
опытов.
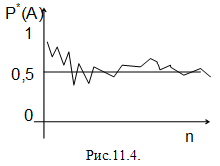
На рис.11.4 в графической форме представлены результаты
опытов по бросанию монеты и определению через равное число проведенных бросков
относительной частоты события А - появления герба. Как видно из рисунка, с
увеличением числа опытов n относительная частота появления герба приближается к
величине 0,5, что согласуется с теоретическим вычислением вероятности этого
события по формуле для классического определения вероятности (11.1).
Конкретный смысл вероятности заключается в том, что она
определяет среднюю относительную частоту появления какого либо события в длинных
сериях испытаний. Если мы говорим, что вероятность какого-либо события
составляет 0,1, то следует ожидать, что при увеличении числа испытаний это
событие будет наступать приблизительно в 10 % случаев от общего числа испытаний.
12.2. Законы распределения случайных величин
Законом распределения случайной величины называется любое правило (таблица,
график, функция), позволяющее находить вероятности всевозможных событий,
связанных со случайной величиной (например, вероятность того, что она примет
какое то значение или попадет на какой то интервал).
Различают теоретические и эмпирические законы распределения случайных величин. В
первом случае оценка возможных значений случайной величины производится при
помощи вероятностей, а во втором при помощи относительных частот.
Наиболее простую форму можно придать закону распределения
дискретной случайной величины. Для этого достаточно перечислить возможные
значения случайной величины X: x1, x2, ... xn и соответствующие им вероятности.
Рядом распределения дискретной случайной величины X называется таблица (табл.11.2), в
верхней строке которой перечислены в порядке возрастания все возможные значения
случайной величины X: x1, x2, ... xn, а в нижней вероятности этих
значений: p1, p2, ... pn, где pi
= P(X = xi) -
вероятность того, что в результате опыта случайная величина X примет значение xi
(i = 1, 2, ... n).
Таблица 11.1

Так как события (X=x1), (X=x2),
... (X=xn)
несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в
нижней строке таблицы 1.2 равна единице:
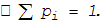
Ряд распределения могут быть построены только для дискретной
случайной величины. Наиболее общей формой закона распределения, пригодной для
всех случайных величин является функция распределения.
Функцией распределения случайной величины
X называется вероятность
того, что она примет значение меньшее или равное заданного x:
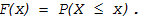 (11.6)
(11.6)
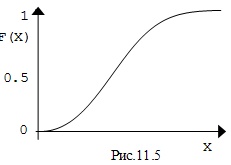
Функция распределения F(x) любой случайной величины есть неубывающая
функция своего аргумента, значение которой заключено между 0 и 1:
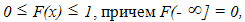
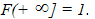
Зная функцию распределения F(x) случайной величины
X, можно вычислять
вероятности любых событий, с нею связанных (рис.11.5). Например, очевидно, что
вероятность попадания случайной величины в заданный интервал от x1 до x2 равна приращению функции
распределения на этом участке, т.е.
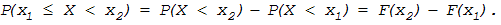 (11.7)
(11.7)
Интегральная функция распределения непрерывной случайной
величины является дифференцируемой функцией.
Первая производная от функции распределения называется
плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x:
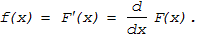 (11.8)
(11.8)
Очевидно, вероятность попадания случайной величины X на
участок от x1 до x2 равна определенному интегралу
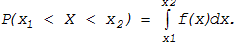 (11.9)
(11.9)
Формула (12.9) дает возможность выразить функцию
распределения через плотность распределения:
F(x)=
P(X<x)=
P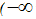 <
X < x2)=
<
X < x2)=
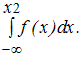 (11.10)
(11.10)
При статистической обработке результатов совокупности
измерений, в которой фигурирует непрерывная случайная величина, оперируют со
статистическими аналогами функции распределения, плотности распределения и их
графическими представлениями.
11.3.
Характеристики тенденций процессов производства медицинских услуг
Основными характеристиками тенденций протекания процесса
являются математическое ожидание, медиана и мода.
Группа явлений, объединенных каким-либо общим признаком или
свойством качественного или количественного характера, носит название
статистической совокупности.
Выборкой называется часть членов совокупности,
отобранных для нее для получения сведений о всей совокупности. В этом случае
совокупность, из которой извлекается выборка, называется
генеральной совокупностью.
Во всех случаях применения выборочного
метода наблюдения необходимым условием является репрезентативность полученных
результатов (от французского - representer - отображать),
что означает соблюдение таких условий при исследовании,
при которых все характеристики выборочной совокупности полностью, отражают
свойства генеральной совокупности, поэтому выводы,
полученные при изучении отобранной части явлений, можно
распространить на все явление в целом.
При простой случайной (рандомизированной) выборке отбор
единиц в
выборочную совокупность производится из всей
массы единиц генеральной совокупности в форме случайного
отбора, при котором каждой единице генеральной совокупности обеспечивается
одинаковая вероятность быть выбранной. Обеспечить случайность отбора можно либо
способом жеребьевки, либо с помощью специальных таблиц
случайных чисел или механического
отбора случаев оказания медицинской помощи из генеральной совокупности
Типическая случайная выборка (стратификация) - разделение совокупности по выбранным
признакам (формирование однородных групп по диагнозу, виду помощи, др.). Если
исследуемая совокупность неоднородна по диагнозу (например, клиническое
отделение) вначале осуществляется ее стратификация или типологическая
группировка. Для каждой типической группы формируется простая рандомизированная
выборка, совокупность этих выборок составит типологическую (стратифицированную)
рандомизированную выборку (рис. 11.6).
Беря выборку из генеральной совокупности и вычисляя ее
статистические характеристики, можно с некоторым приближением считать, что они
по своим величинам будут близки к соответствующим параметрам генеральной
совокупности, т.е. будут являться их оценками. Но для того, чтобы эти оценки достаточно
правильно и близко характеризовали параметры генеральной совокупности,
необходимо, чтобы они удовлетворяли трем требованиям: были состоятельными,
эффективными и несмещенными.
Состоятельной называют статистическую оценку, которая
при
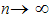 стремится
по вероятности к оцениваемому параметру.
стремится
по вероятности к оцениваемому параметру.
Несмещенной называют статистическую оценку,
математическое ожидание которой равно оцениваемому параметру.
Эффективной называют статистическую оценку, которая
при заданном объеме выборки имеет наименьшую дисперсию.
В медицине и здравоохранении часто используются выражаемые
числовыми значениями признаки, которые могут принимать различные числовые
значения у разных единиц совокупности. Параметры генеральной совокупности чаще
всего оцениваются выборочным средним арифметическим, выборочной медианой и
выборочной модой.

Рис. 11.6. Стратифицированная рандомизированная выборка для
планирования экспертизы медицинских услуг в многопрофильном ЛПУ
Ряд, в котором упорядоченно сопоставлены (по степени
возрастания или убывания) варианты и соответствующие им частоты называется
вариационным, отдельные количественные выражения признаки - вариантами (x), а числа, показывающие как часто
варианты повторяются – частотами (Р).
Мода (Мо)
– значение случайной величины, которому соответствует максимальная вероятность
для дискретных или плотность распределения f(x) для непрерывных.
Выборочная мода – это такое значение х, которое имеет
максимальную частоту.
Медианой (Ме)
случайной величины называется такое ее значение, для которого функция
распределения равна 0,5. Геометрически медиана - это абсцисса той точки на оси
0x, для которой площади, лежащие слева и справа от нее, одинаковы и равны 0,5.
Выборочная медиана – это результат наблюдения, который
занимает срединное положение в выборке с четным числом наблюдений.
Математическое ожидание, мода и медиана являются
характеристиками положения, фиксирующими положение случайной величины на
числовой оси, т.е. некоторое среднее, ориентировочное значение случайной
величины около которого группируются ее возможные значения. Средняя
арифметическая для вариационного ряда, в котором каждая варианта встречается
только один раз называется средней арифметической простой. Она определяется по
формуле:
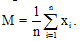 (11.11)
(11.11)
М – средняя арифметическая;
х – значение вариационного признака;
n – общее число
наблюдений.
Если одна или несколько вариант повторяются, то вычисляют среднюю
арифметическую взвешенную:
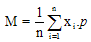 (11.12)
(11.12)
Р-частота значения вариационного признака.
Средняя арифметическая является состоятельной, несмещенной и
эффективной оценкой.
Оценкой для дисперсии случайной величины X является статистическая дисперсия, которая
для простой средней арифметической вычисляется по формуле 11.13, а для взвешенной 11.14.
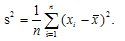 (11.13)
(11.13)
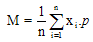 (11.14)
(11.14)
х – значение вариационного признака;
n – общее число
наблюдений.
Р – частота признака.
Оценкой среднего квадратического отклонения является корень
из статистической дисперсии
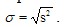 . (11.14)
. (11.14)
Можно использовать приближенный способ расчета среднего
квадратического отклонения по размаху (амплитуде) вариационного ряда. Размах –
это разность между наибольшим и наименьшим значением х в выборке.
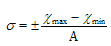 (11.15)
(11.15)
А – коэффициент для определения σ, соответствующий числу наблюдений
(табл.11.3).
При изучении генеральной совокупности для ее числовой
характеристики достаточно рассчитать среднюю арифметическую и среднее
квадратическое отклонение. На практике, как правило, мы имеем дело с выборочной
совокупностью. При определении степени точности выборочного исследования
оценивается величина ошибки, которая может произойти в процессе выборки. Средняя
ошибка средней арифметической (m)
определяется по формуле:
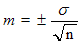 (11.16)
(11.16)
Среднюю ошибку средней арифметической можно вычислить по
амплитуде:
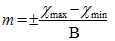 (11.17)
(11.17)
В – коэффициент для определения ошибки, соответствующий числу наблюдений
(табл.11.3).
При оценке полученного результата по размеру средней ошибки
пользуются доверительным коэффициентом (t), который дает возможность определить
вероятность правильного ответа, т.е. он указывает на то, что полученная величина
ошибки выборки будет не больше действительной ошибки, допущенной при сплошном
наблюдении (табл.11.2).
Таблица 11.2. Оценка полученного результата по средней ошибке
|
Доверительный
коэффициент
|
Достоверность
результата
|
Вероятность ошибки
(p)
|
|
t1 = M ± 1m
|
68,3% (0,683)
|
0,317
|
|
t2 = M ± 2m
|
95,5% (0,955)
|
0,05
|
|
t2,6 =
M ± 2,6m
|
99,0% (0,990)
|
0,010
|
|
t3 =
M ± 3m
|
99,7% (0,997)
|
0,003
|
|
t3,3 =
M ± 3,3m
|
99,9 (0,999)
|
0,001
|
В медико-статистических исследованиях обычно используют
доверительную вероятность, равную 95,5-99% (t = 2 или 3).
Таблица 11.3. Вычисление сигмы (σ) и ошибки (m) по амплитуде
|
Число наблюдений
|
Коэффициент для сигмы , А
|
Коэффициент для ошибки , В
|
Число наблюдений
|
Коэффициент для сигмы, А
|
Коэффициент для ошибки, В
|
|
1
|
-
|
-
|
32
|
4,14
|
23,40
|
|
2
|
1,13
|
1,60
|
34
|
4,19
|
24,6
|
|
3
|
1,69
|
2,93
|
36
|
4,24
|
25,5
|
|
4
|
2,06
|
4,12
|
38
|
4,28
|
26,4
|
|
5
|
2,33
|
5,20
|
40
|
4,32
|
27,30
|
|
6
|
2,53
|
6,21
|
50
|
4,50
|
31,8
|
|
7
|
2,70
|
7,16
|
60
|
4,64
|
35,9
|
|
8
|
2,85
|
8,05
|
70
|
4,76
|
39,8
|
|
9
|
2,97
|
8,9
|
80
|
4,85
|
43,3
|
|
10
|
3,08
|
9,70
|
90
|
4,94
|
46,9
|
|
11
|
3,17
|
10,50
|
100
|
5,01
|
50,10
|
|
12
|
3,26
|
11,20
|
120
|
5,15
|
56,3
|
|
13
|
3,34
|
12,00
|
140
|
5,26
|
62,3
|
|
14
|
3,41
|
12,70
|
160
|
5,35
|
67,6
|
|
15
|
3,47
|
13,4
|
180
|
5,43
|
73,0
|
|
16
|
3,53
|
14,10
|
200
|
5,50
|
77,8
|
|
17
|
3,59
|
14,8
|
220
|
5,57
|
82,6
|
|
18
|
3,64
|
15,4
|
240
|
5,61
|
87,0
|
|
19
|
3,69
|
16,10
|
260
|
5,68
|
91,7
|
|
20
|
3,74
|
16,7
|
280
|
5,72
|
95,7
|
|
22
|
3,82
|
17,9
|
300
|
5,77
|
100,0
|
|
24
|
3,90
|
19,0
|
320
|
5,80
|
103,8
|
|
26
|
3,96
|
20,2
|
340
|
5,84
|
107,9
|
|
28
|
4,03
|
21,2
|
360
|
5,88
|
111,5
|
|
30
|
4,09
|
22,4
|
380
|
5,92
|
115,2
|
Используя значение ошибки можно рассчитать требуемое число наблюдений для
выборочной совокупности:
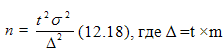 (11.18)
(11.18)
Например:
Средняя длительность лечения в стационаре составило 14,8 дн.,
σ =±1,8 дн., m=±0,16. Нужно определить, сколько необходимо
исследовать больных при t= 3.
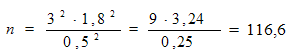
Таким образом, необходимо исследовать 116-117 больных.
Для получения высоко достоверных показателей нельзя
беспредельно увеличивать число наблюдений, да и конкретные материалы
представляют собой четко ограниченные по численности группы наблюдений.
Показатель (средняя величина) считается достоверным, если он
в 2 раза, а лучше в 3 раза превышать свою среднюю ошибку.
В нашем примере средняя величина 14,8 дней
во много раз превышает свою утроенную
ошибку (14,8>0,16·3). Следовательно, полученный результат можно считать
достоверным.
11.4.
Распределения биноминальное, нормальное и Пуассона
Биномиальное распределение. По
отдельным членам бинома можно определить число дефектов в выборке:
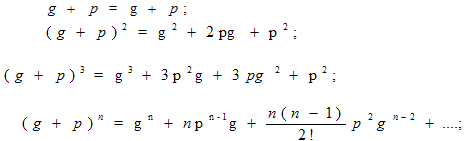
(11.19)
Рассмотрим пример. Предположим, что выявлено 4% дефектов.
Тогда р=0,04, g= 1 -
p = 0,96.
Таким образом, вероятность того, что в
выборке из 50 единиц наблюдения не будет брака равна 0,9650.
Вероятность выявления одного дефекта в данной выборке равна
50(096)49(0,04).
Если производится n независимых выборок, в каждом из которых
событие А может появиться в вероятностью p, то вероятность того, что в n опытах
событие А появится m раз равна
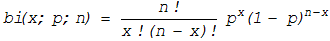
(11.20)
где символ n! обозначает факториал и выражает произведение
натуральных чисел 1, 2, 3 ... n; при этом 0!=1.
Применительно к управлению качеством данная формула позволяет
определить вероятность того, что при контроле выборки объемом n из генеральной
выборки с долей дефектных единиц p (уровень дефектности), в ней окажется x
дефектных случаев. При такой схеме контроля изменяется вероятность p.
Этим пренебрегают, если объем
выборки
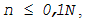 где N - объем генеральной совокупности, что
чаще всего имеет место на практике.
где N - объем генеральной совокупности, что
чаще всего имеет место на практике.
Математическое ожидание, дисперсия и среднее квадратическое
отклонение при этом при этом:
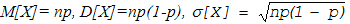 (11.21)
(11.21)
np – среднее число дефектных случаев
Закон нормального распределения (Закон Гаусса) играет исключительно важную роль в теории
вероятностей и занимает среди других законов распределения особое положение.
Случайная величина X распределена по нормальному закону (Закону Гаусса) с
параметрами m и s
, если плотность ее
распределения имеет вид:
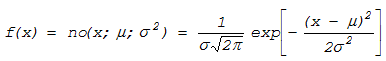 (11.22)
(11.22)
Широкое применение закона нормального распределения находит
свое теоретическое обоснование в теореме, которая была доказана русским
математиком Ляпуновым, следствие которой определяется так: если случайная
величина X представляет
собой сумму большого числа взаимно независимых случайных величин X1, X2, ... Xn, влияние
каждой из которых на всю сумму мало, то независимо от того, каким законам
распределения подчиняются слагаемые X1, X2, ... Xn сама величина будет иметь
распределение вероятностей, близкое к нормальному, и тем точнее, чем больше
число слагаемых.
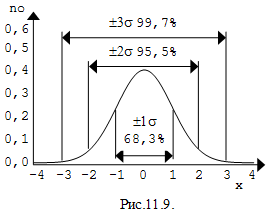
Кривая нормального распределения описывает частотное
распределение результатов повторных измерений одного и того же физического
объекта полученного одним и тем же методом. Разброс значений отражает только
случайную вариацию. Кривая нормального распределения имеет форму колокола. Её
математическое свойство таково, что примерно 68 % результатов измерений лежит в
пределах одного стандартного отклонения и около 95 % – в пределах двух
стандартных отклонений.
На практике нормальное распределение имеет место, если
случайная величина - признак качества является результатом действия множества
величин влияния. При определенных условиях нормальное распределение можно
применить как приближение биномиального распределения или распределения
Пуассона.
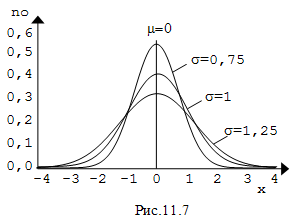
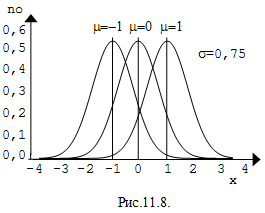
При изменении µ кривая no (x;m;s
2), не изменяя
своей формы, просто будет смещаться вдоль оси абсцисс (рис.11.8). Изменение s
приводит к изменению формы кривой (рис.11.7).
Для практических целей важное значение имеют вероятности
попадания нормально распределенной случайной величины в интервалы из таблицы
11.3.
Границы интервалов µ± 1s
и µ±
2s являются
точками перегиба кривой нормального распределения.
Таблица 11.4
|
Интервал
попадания
|
Вероятность попадания в
интервал, %
|
|
µ ± 1s
|
68,3
|
|
µ ± 1,,96s
|
95,0
|
|
µ ± 2,0s
|
95,5
|
|
µ ± ,2,58s
|
99,0
|
|
µ ± 3,0s
|
99,7
|
|
µ ± 3,29s
|
99,9
|
Закон Пуассона (Закон редких событий)
Если мы хотим найти вероятность маловероятного события на
единицу, то необходимо воспользоваться распределением Пуассона:
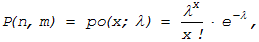 (11.23)
(11.23)
где параметр l
представляет собой математическое ожидание
числа событий на единицу. Если рассматриваемой единицей является выборка из
произведенных услуг, то l = np
(число дефектных случаев в
выборке), а уравнение (11.23) определяет собой распределение редких
событий.
Математическое ожидание и дисперсия для данного закона
определяются по выражениям:
M[X]= D[X]= l . (11.24)
Пример: количество дефектов на одного больного; число
жалоб на одного работника; число ошибок на 1000 исследований; количество
превышений сроков ожидания госпитализации и т.п.
Таблица 11.5. дает вероятности того, что r или более
случайных событий появятся в некотором интервале при среднем числе таких событий
в интервале, равном m, т.е.
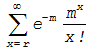
Таблица 11.5. Накопленные вероятности распределения Пуассона
|
m =
|
0,1
|
0,5
|
1
|
2
|
3
|
4
|
5
|
10
|
15
|
20
|
|
r=0
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
|
1
|
0,0952
|
0,3935
|
0,6321
|
0,8647
|
0,9502
|
0,9817
|
0,9933
|
1,0000
|
1,0000
|
1,0000
|
|
2
|
0,0047
|
0,0902
|
0,2642
|
0,5940
|
0,8009
|
0,9084
|
0,9596
|
0,9995
|
1,0000
|
1,0000
|
|
3
|
0,0002
|
0,0144
|
0,0803
|
0,3233
|
0,5768
|
0,7619
|
0,8753
|
0,9972
|
1,0000
|
1,0000
|
|
4
|
0,0000
|
0,0018
|
0,0190
|
0,1429
|
0,3528
|
0,5665
|
0,7350
|
0,9897
|
0,9998
|
1,0000
|
|
5
|
0,0000
|
0,0002
|
0,0037
|
0,0527
|
0,1847
|
0,3712
|
0,5595
|
0,9707
|
0,9991
|
1,0000
|
|
6
|
0,0000
|
0,0000
|
0,0006
|
0,0166
|
0,0839
|
0,2149
|
0,3840
|
0,9329
|
0,9972
|
0,9999
|
|
7
|
0,0000
|
0,0000
|
0,0001
|
0,0045
|
0,0335
|
0,1107
|
0,2378
|
0,8699
|
0,9924
|
0,9997
|
|
8
|
0,0000
|
0,0000
|
0,0000
|
0,0011
|
0,0119
|
0,0511
|
0,1334
|
0,7798
|
0,9820
|
0,9992
|
|
9
|
0,0000
|
0,0000
|
0,0000
|
0,0002
|
0,0038
|
0,0214
|
0,0681
|
0,6672
|
0,9626
|
0,9979
|
|
10
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0011
|
0,0081
|
0,0318
|
0,5421
|
0,9301
|
0,9950
|
|
11
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0003
|
0,0028
|
0,0137
|
0,4170
|
0,8815
|
0,9892
|
|
12
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0001
|
0,0009
|
0,0055
|
0,3032
|
0,8152
|
0,9786
|
|
13
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0003
|
0,0020
|
0,2084
|
0,7324
|
0,9610
|
|
14
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
0,0001
|
0,0007
|
0,1355
|
0,6368
|
0,9339
|
11.5. Перспективы использования контрольных карт в экспертных оценках качества в медицине
Поведение любого производственного процесса, в том числе и процесса оказания
медицинской помощи, можно представить как функцию большого
числа входных параметров (исходное состояние основных
производственных фондов, состояние пациента, калибровка (точность) технологического и
диагностического оборудования,
квалификации медицинского персонала и т.д.).
Значения этих параметров могут иметь колебания двух видов:
случайные, которые не могут быть устранены, и неслучайные (систематические),
которые могут быть устранены, либо сведены к минимуму.
Результатом этих колебаний является разброс уровня качества
процесса производства медицинских
услуг. Если
колебания входных параметров носят только случайный характер, то о производственном процессе говорят как о налаженном. Пределы качества процесса называются его естественными границами и рассматриваются как мера его технических
возможностей.
При неслучайном характере колебаний входных параметров
производственного процесса уровень его качества может выйти за естественные
границы, результатом чего станут медицинские услуги, не отвечающая заданным стандартным требованиям.
Контрольные карты служат для наглядного отображения
протекания производственного процесса и своевременного распознавания его
неслучайных отклонений или нарушений.
Одним из важнейших качеств процесса является его стабильность. Индекс
возможности процесса.
Для проведения предварительного
анализа процесса можно поступать двумя способами:
- из процесса
берут большую
выборку и
получают оценки
для
m
и
s в виде
обычного
среднего
значения и
статистической
дисперсии по
формулам
(12.11),
(12.13),
(12.14);
- из процесса
берут
последовательно
k выборок по n
единиц в каждой
и далее получают
оценки для
m
и
s по
следующим
формулам:
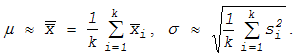 (11.25)
(11.25)
Имея оценки для m и s определяют
показатели возможностей процесса (Ср). Он характеризует соотношение поля
рассеяния процесса и величину допуска:
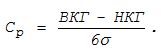 (11.26)
(11.26)
В этой формуле ВКГ и НКГ являются верхней и нижними контрольными границами.
Им могут соответствовать наибольший предельный размер и наименьший предельный
размер, верхнее отклонение и нижнее отклонение. Разность любых этих значений
дает величину допуска на признак
качества. Значения Ср превышающие 1, указывают на то, что в
пределах заданного поля допуска находятся 3 среднеквадратических отклонения. Для
обеспечения надежной работы процесса в рамках установленных пределов статистики
советуют добиваться значения Ср=2.
Значение Ср=1 не дает гарантии от возникновения дефектов
из-за возможного смещения кривой распределения относительно центра допуска. Для
оценки таких ситуаций используют другой показатель - индекс настройки процесса:
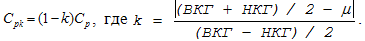 (11.27)
(11.27)
Индекс возможности процесса и индекс настройки процесса
используются совместно для определения статуса процесса. Так в машиностроении
считается нормой, если Ср ≥ Срk
≥1,33, что же относительно
процесса оказания медицинской помощи, то индекс его настройки имеет ограниченное
применение.
Итак, контрольная карта – это разновидность графика, однако
она отличается от обычного графика наличием линий, называемых контрольными
границами или границами регулирования. Эти контрольные границы обозначают
ширину разброса, образующегося в обычных условиях течения процесса производства медицинских услуг, т.е. определяют его естественные
границы. Если все точки на контрольной карте входят в область, ограниченную
контрольными границами, это указывает на то, что процесс протекает в
относительно постоянных условиях, т.е. на стабильность процесса. Если же
значение показателя качества вышло за эти границы, то
возможны два варианта событий:
- выпадающее
значение - хотя
оно и относится
к генеральной
совокупности, но
может выпасть на
основании
выбранной
статистической
надежности; в
этом случае в
технологический
процесс
вмешиваться не
рекомендуется;
- значение вышло
за границы
регулирования,
так как что-то
изменилось, т.е.
в ходе процесса
возникли
причины,
нарушившие его
стабильность.
Следовательно,
выпадающее
значение
относится к
другой
генеральной
совокупности и
выход за границы
регулирования не
случайный. В
этом случае
необходимо
исследовать
причину
нарушения
процесса и
устранить ее.
Для того чтобы различать эти два случая, необходимо провести
довольно простой анализ состояния процесса на предшествовавшем небольшом отрезке
времени. Если предыдущие значения показателя качества находятся довольно близко
к границе регулирования или замечается такая тенденция, при которой отдельные
значения все больше приближаются к границе регулирования, то вполне вероятно,
что процесс протекает с систематическими отклонениями. Если же предыдущие
значения беспорядочно рассеяны между верхней и нижней границами регулирования,
то чаще всего отклонения будет случайным.
Если показатели качества могут быть выражены количественными
данными, то используют так называемые контрольные карты по количественному
признаку. В тех случаях, когда показатели качества определяются
качественными данными, типа “качественно” и “некачественно” используют
контрольные карты по альтернативному признаку.
Применению карт должен предшествовать предварительный
статистический анализ процесса и устранение выявленных недостатков. Без этого
внедрение контрольных карт не имеет смысла. При неустойчивом и, следовательно,
не отлаженном процессе статистическое регулирование сведется к беспрерывным
остановкам и отысканию причин.
Контрольные карты по
количественному признаку.
Наибольшее распространение получили
контрольные карты
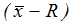 среднего арифметического и размаха и
контрольные карты
среднего арифметического и размаха и
контрольные карты
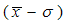 среднего арифметического и среднего
квадратического отклонения. Построение контрольных карт
достаточно сложный и включает несколько этапов.
среднего арифметического и среднего
квадратического отклонения. Построение контрольных карт
достаточно сложный и включает несколько этапов.
Следствие из теоремы Ляпунова позволяет сделать вывод о том,
что если изучаемая величина является суммой большого числа независимых случайных
слагаемых, то хотя последние нам не известны, часто можно заранее считать, что
наша величина имеет нормальное распределение. В данном случае лучше ограничиться
моделью нормального распределения.
Если случайная величина X имеет нормальное распределение, то
вероятность попадания ее в интервал
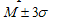 превышает 99%. При осуществлении выборок
из генеральной совокупности распределение выборочных средних
превышает 99%. При осуществлении выборок
из генеральной совокупности распределение выборочных средних
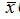 будет также
нормальным.
будет также
нормальным.
Устанавливаем верхнюю границу регулирования -
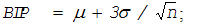 ; (11.28)
; (11.28)
нижнюю границу регулирования -
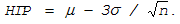 . (11.29)
. (11.29)
Выбор интервалов
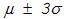 для установления границ регулирования
используется в англоязычных странах. В европейской практике чаще используют
интервал
для установления границ регулирования
используется в англоязычных странах. В европейской практике чаще используют
интервал 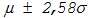 , который содержит ровно 99 % значений
случайной величины. Кроме того европейцы наносят на контрольную карту
предупредительные границы, используя интервал
, который содержит ровно 99 % значений
случайной величины. Кроме того европейцы наносят на контрольную карту
предупредительные границы, используя интервал
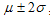 , который содержит 95,5 % случайной
величины.
, который содержит 95,5 % случайной
величины.
Формулами (11.28) и (11.29) пользуются, когда известны генеральное
среднее m и генеральное среднее
квадратическое отклонение. Если они неизвестны, то используют их оценки. Для
генерального среднего в качестве оценки при построении контрольных карт
используют среднее выборочных средних:
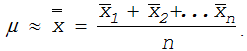 (11.30)
(11.30)
Для оценки генерального среднего квадратического отклонения
используют известное соотношение R=dns, где dn
- константа преобразования Хартли. Значение dn зависит только от объема выборки (табл.11.6).
Таблица 11.6
|
n
|
5
|
6
|
7
|
8
|
9
|
10
|
|
dn
|
2,33
|
2,53
|
2,70
|
2,85
|
2,97
|
3,04
|
Соответственно, оценкой для генерального среднего
квадратического отклонения будет выражение
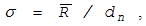 ,
(11.31)
,
(11.31)
где 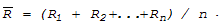 . (11.32)
. (11.32)
Размах Rn представляет собой разность наибольшего и
наименьшего значения выборки.
Используя оценки (11.31) и (11.32), получаем контрольные пределы:
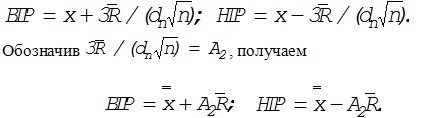 (11.33)
(11.33)
Аналогичным образом определяются пределы регулирования для
контрольных карт размахов (табл.11.7).
Значения коэффициентов A2 , D4 , D3
приведены в табл. 11.8. Их значения зависят от объема выборки n.
Таблица 11.7. Контрольные пределы контрольных карт по количественному
признаку
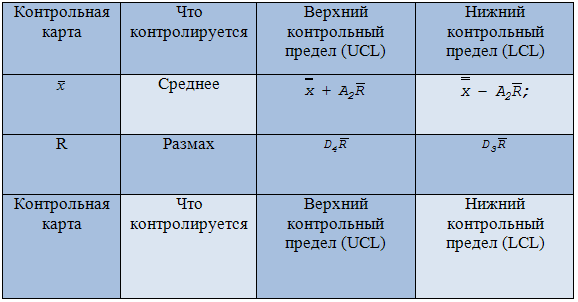
Таблица 11.8. Коэффициенты для контрольных карт средних арифметических значений и размаха
|
n
|
А
|
A2
|
D1
|
D4
|
D3
|
|
5
|
1,342
|
0,577
|
0
|
2,115
|
0
|
|
6
|
1,225
|
0,483
|
0
|
2,004
|
0
|
|
7
|
1,134
|
0,419
|
0,205
|
1,924
|
0,076
|
|
8
|
1,061
|
0,373
|
0,387
|
1,864
|
0,136
|
|
9
|
1,000
|
0,337
|
0,546
|
1,816
|
0,184
|
|
10
|
0,949
|
0,308
|
0,687
|
1,777
|
0,223
|
|
11
|
0,905
|
0,285
|
0,812
|
1,744
|
0,256
|
|
12
|
0,866
|
0,266
|
0,924
|
1,716
|
0,284
|
|
13
|
0,832
|
0,249
|
1,026
|
1,692
|
0,308
|
|
14
|
0,802
|
0,235
|
1,207
|
1,671
|
0,329
|
|
15
|
0,775
|
0,223
|
1,207
|
1,652
|
0,348
|
|
16
|
0,750
|
0,212
|
1,287
|
1,636
|
0,364
|
|
17
|
0,728
|
0,203
|
1,359
|
1,621
|
0,379
|
|
18
|
0,707
|
0,194
|
1,426
|
1,608
|
0,392
|
|
19
|
0,688
|
0,187
|
1,490
|
1,596
|
0,404
|
|
20
|
0,671
|
0,180
|
1,549
|
1,586
|
0,414
|
Пример. Проведен статистический анализ средней
длительности лечения пациентов в стационаре. Отобрано 25 выборок объемом
n=5 каждая. Данные контроля
представлены в табл. 11.8.
|
Номер выборки
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
R
|
|
1
|
12
|
15
|
14
|
11
|
13
|
13,0
|
4
|
|
2
|
13
|
13
|
16
|
12
|
14
|
13,6
|
4
|
|
3
|
15
|
13
|
16
|
14
|
14
|
14,4
|
3
|
|
4
|
11
|
14
|
14
|
13
|
15
|
13,4
|
4
|
|
5
|
13
|
15
|
17
|
12
|
12
|
13,8
|
5
|
|
и т.д.
|
|
|
|
|
|
|
|
Таблица
11.8
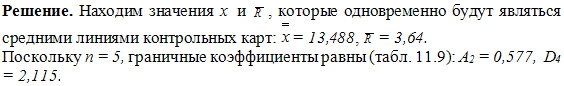

По полученным данным строим контрольную карту.
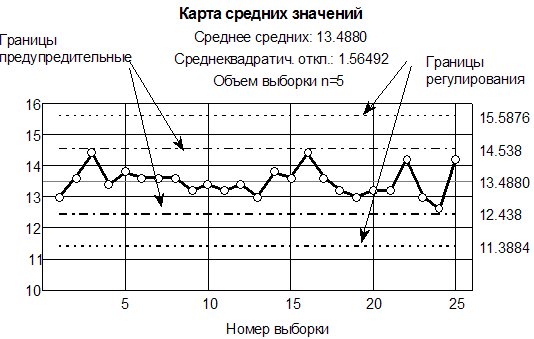
Рис.11.9.
Контрольная карта средних значений процесса
Ход контрольной карты представляет динамическую
характеристику процесса. В идеале точки ложатся равномерно относительно средней
линии и преимущественно ближе к ней. Стабильное поведение процесса в рамках
контрольных границ – лучшее подтверждение результативности управления
производственным процессом.
Контрольные карты по
альтернативному признаку. В тех случаях, когда контроль по
альтернативному признаку применяется для определения состояния технологического
процесса, налаженного или разлаженного, соответствующий метод статистического
регулирования технологических процессов называют методом учета дефектов.
Наиболее распространенными для метода учета дефектов являются
контрольные карты доли дефектных случаев, называемые p - картами, и количества дефектов на единицу
продукции, называемые с -
картами. Два других вида
контрольных карт этой группы - контрольные карты
количества дефектных единиц np-карты и среднего
числа дефектов u-карты аналогичны p и c картам.
В p-карте подсчитывается доля дефектных единиц в выборке. Она
применяется, когда объем выборки – переменный.
При работе с р-картами (биномиальное
распределение) периодически берут выборки (необязательно одинакового объема) и
вычисляют выборочную долю дефектных единиц, которую наносят на график. При
выходе точки за границы регулирования производственный процесс останавливают.
Для расчета контрольных границ используют величину, полученную по результатам
взятия нескольких выборок
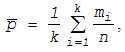 , (11.34)
, (11.34)
где 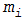 - число дефектов в i-той выборке; n -
объем одной выборки; k - число выборок для предварительного исследования.
- число дефектов в i-той выборке; n -
объем одной выборки; k - число выборок для предварительного исследования.
Контрольные границы рассчитывают по формулам из таблицы 11.9.
При расчете контрольных границ по методу
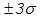 нижняя контрольная граница может
получиться отрицательной. В этом случае ее принимают равной нулю.
нижняя контрольная граница может
получиться отрицательной. В этом случае ее принимают равной нулю.
Таблица 11.9
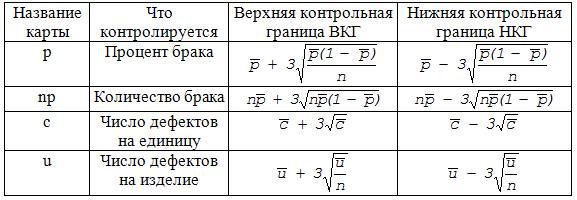
Контрольная карта числа дефектных единиц продукции в выборке np-карта позволяет непосредственно отмечать
количество дефектных единиц, а не рассчитывать их долю.
Для расчета контрольных границ из предварительного исследования определяют
величину
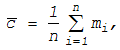 (11.35)
(11.35)
где 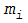 - число дефектов в одной выборке; n -
число выборок.
- число дефектов в одной выборке; n -
число выборок.
Контрольные карты числа дефектов на единицу продукции
u-карты используют при взятии для регулирования нескольких видов
дефектов. Дефекты могут быть различного рода, но они должны быть независимыми
друг от друга и приблизительно одинаковой значимости. Применяют, когда выборки
состоят из нескольких единиц, причем число единиц может меняться. Для каждой выборки
вычисляют соотношение
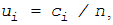 , где
, где
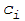
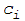 - общее количество наблюдаемых в выборке
дефектов; n - число единиц в выборке.
- общее количество наблюдаемых в выборке
дефектов; n - число единиц в выборке.
11.6. Обобщение
результатов исследования производственного процесса
При формировании программ качества необходимо учитывать и
оценивать четыре следующих компонента: соблюдение медицинских технологий
(реализация стандартного процесса производства медицинских услуг), оптимальность использования
ресурсов, риск травм и заболеваний в результате медицинского вмешательства,
удовлетворенность потребителя (пациента) медицинским обслуживанием.
Для предупреждения систематической ошибки при проведении
экспертизы вследствие отбора случаев в выборку применяются такие методические
приемы как рандомизация, стратификация и др.
Для того чтобы с вероятностью р=0,95 в выборку попали случаи
ненадлежащего КМП, которые в совокупности составляют не менее 15%, к
количественному составу выборки предъявляются требования согласно табл. 11.10.
Таблица 11.10. Определение размера выборки при предполагаемой доле случаев ненадлежащего КМП в генеральной совокупности не менее 15%
|
Генеральная совокупность
|
Выборка p=0.95
|
|
Общее количество случаев
|
Количество случаев ненадлежащего КМП
|
Количество случаев
|
% случаев от
генеральной совокупности
|
|
До 19
|
1-2
|
До 19
|
100
|
|
20
|
3
|
12
|
60
|
|
40
|
6
|
15
|
37,5
|
|
60
|
9
|
16
|
26,6
|
|
80
|
12
|
17
|
21
|
|
100
|
15
|
18
|
17
|
|
120
|
18
|
18
|
15
|
|
140
|
21
|
18
|
12,8
|
|
180
|
27
|
18
|
10
|
|
200 - 500
|
30-75
|
18
|
9 - 3,6
|
Предложенный способ формирования малых выборок ориентирован
главным образом на построение стратифицированных рандомизированных выборок. При
этом общий объем выборочной совокупности, как правило, составляет не менее
10-14% от генеральной совокупности.
На этапе статистической обработки экспертных данных для
предупреждения систематической ошибки исследования применяются методические
приемы: стратификация, стандартизация и др.
Стратификация - экспертных протоколов осуществляется по
тем же признакам, что и стратификация генеральной совокупностью.. Это процесс
сортировки данных согласно некоторым критериям и или переменным, результаты,
которого часто представляются в виде диаграмм и графиков. В результате чего
появляется возможность сравнения разных групп по количественным показателям КМП
(риски и структура) и структуре врачебных ошибок. Стратификация – основа для
других инструментов, таких диаграмма рассеивания или анализ Парето.
При дальнейшем анализе стратификация (по факторным и
результативным признакам) применяется как самостоятельный метод статистического
контроля и управления качеством процессов.
Стандартизация - способ математической коррекции данных для
восстановления репрезентативности стратифицированной рандомизированной выборки
исследуемой совокупности. Для расчета стандартизированных количественных
показателей КМП используется формула получения средних взвешенных величин:
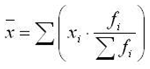
где x - показатель КМП по
стратифицированной рандомизированной выборке; xi
- i-й вариант показателя (i = 1,…,
n) по типической группе; fi - доля типической группы в структуре
совокупности (в %).
Графические способы оценки КМП
К графическим приемам, которые используются для выявления
проблемы, относятся такие методы, как диаграмма алгоритма процесса, лист
подсчета, метод номинальной групп и др. Для анализа проблемы следует
воспользоваться гистограммой, контрольным графиком, диаграммой рассеивания и др.
Диаграмму Парето, причинно- следственную диаграмму, линейный график можно
применять как на фазе выявления, так и на фазе анализа проблемы.
Лист подсчета используется для сбора выборочных
данных с целью обнаружения закономерностей функционирования процесса. Лист
подсчета используется, чтобы ответить на вопрос «Как часто происходит данное
событие?» Для этого необходимо прийти к соглашению о том, какое событие мы
наблюдаем, за какой период времени мы хотим собрать данные. Следует разработать
ясный и удобный бланк для записи данных, систематически и объективно их
собирать.
На получение и занесение данных должно быть отведено
соответственное время. Особое внимание уделяется тому, чтобы наблюдения выборка
максимально точно отражали действительное положение дел, чтобы процесс
составления выборки был нетрудоемким.
Анализ Парето позволяет определить группы (выделенные во
время стратификации), вносящие наибольший вклад в ненадлежащее состояние КМП и
др. Анализ Парето ранжирует отдельные области по важности, значимости и
призывает выявить и в первую очередь устранить те причины, которые вызывают
наибольшее количество проблем.
Поиск решения этих проблем начинают с их классификации по
отдельным факторам (проблемы, относящиеся к оборудованию, к квалификации врачей,
и т.д.), сбора и анализа данных отдельно по группам проблем. Чтобы выяснить,
какие из этих факторов являются основными, строят диаграмму Парето и проводят
анализ диаграммы. Парето показал, что очень часто большая часть проблем
обуславливается небольшой частью факторов.
Диаграмма Парето используется и в противоположном случае,
когда положительный опыт отдельных подразделений хотят внедрить во всей
организации. С помощью диаграммы Парето выявляют основные причины успехов и
широко пропагандируют эффективные методы работы (рис.11.11).

